COUSOTchap1 - 白紙

第１章　準備

１．１　半順序集合と束

　この節は抽象解釈で使われる半順序集合と束に関する初歩的な部分の解説を行う。これについて既に知っている人はこの節を飛ばしてもよい。

１．１．１　半順序集合　

　２つの対象の順序関係は、日常の世界では、それらを大小関係などで一列に並べた時などに使われる（試験の点数順、大学合格者数順など）。日常では当たり前に使っている順序について、数学はその本質的性質を抽出し、半順序と全順序という概念に抽象化した。全順序のほうが日常の順序の感覚に近く、半順序はその条件を緩めたものである。下記は数学的に整理して定義された順序（半順序と全順序）である（数学的定義はどうしても天下り的になるがそれは具体的な例からの抽象化の結果である）；

　半順序は下記(i)～(iii)を満たす関係： L×L→ { true, false }である（注）；

　　　　　(i)反射的、すなわち任意のl∈Lに対して、l 　l

　　　　　(ii)推移的、すなわち任意のｌ₁, l₂, l₃∈Lに対して、(l₁l₂)かつ (l₂l₃)　⇒　l₁l₃

　　　　　(iii)逆対称的、すなわち任意の1₁, l₂∈Lに対して、(l₁l₂)かつ (l₂l₁)　⇒　l₁ = l₂

半順序集合(L,)は、半順序を備えた集合Lである。

　（注）関係は、ｌ₁, l₂∈Lとするとき、l₁l₂が真又は偽であるような関係。

※関係の具体的な例としては、大小関係（≦）や包含関係（⊆）などがある。

（補足）半順序集合の任意の２つの元l₁, l₂に対して、l₁l₂または l₂l₁が成り立つとき、

　　　　　全順序、あるいは線型順序であるという。

１．１．２　半順序集合の上界・下界、上限・下限　

　これも簡単な例を考えれば自然な概念である。例えば半開区間 [0, 1)に属する任意の数xより大きな数は存在する。
これらを上界という。また、そのような数の中で最小のもの（=1)が存在する。これを最小状界または上限という。下記はこのような概念を数学的に記述したものである；

　半順序集合(L,)の部分集合をY、l∈Lとするとき、

　 ① lがYの上界であるとは、任意のl'∈Yに対して l'l

　 ② l₀をYのある上界とするとき、常にll₀を満たすl∈Lが存在するならば、このlをYの最小上界　

　　　または上限であるといい、記号 Yで表す。

　　　は、しばしばjoin演算子と呼ばれ、{ l₁, l₂}はl₁l₂とも表記される。

　同様に、下界、最大下界または下限が定義される；

　 ③ lがYの下界であるとは、任意のl'∈Yに対して ll'

　 ④ l₀をYのある下界とするとき、常にl₀lを満たすl∈Lが存在するならば、このlをYの最大

　　　下界　または下限であるといい、、記号 Yで表す。

　　　は、しばしばmeet演算子と呼ばれ、{ l₁, l₂}はl₁l₂とも表記される。

[例１]下記に区間の集合に対する上限、下限の例を示す；

　Lを区間の集合とし、半順序を区間の包含関係（⊆）とする。例えば、[0, 1]⊆[0,2], [-1, 1]⊆

[-2, 2]など。このとき、(L,⊆）は半順序集合となり、２つの区間の上限、下限は次のようになる；

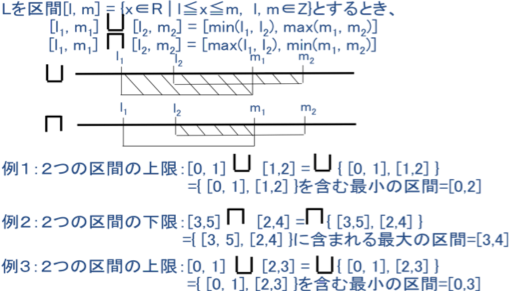
[例２] L={a, b, c, d, e, f, g }とし、線で結ばれた２点x,yに下記の半順序関係(xy⇔yはxより上に

　　　　位置する）があるとする。部分集合Y={b, c, d }とするとき、Yの上界、下界、上限、下限は次の

　　　　ようになる；

　　　　上界: e, f, g、下界：a, b、上限：e ,下限：b

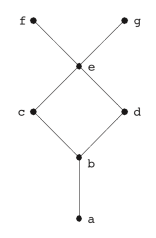
　　　　　　図１．１　半順序関係の例

　　　（注意）Yの上限や下限がもとの集合Yに属しているかどうかはどちらでもかまわない。

１．１．３　束と完備束

（１）束(Lattice)

　半順序集合(L,)が束であるとは、

　任意のl, l'∈Lに対して、その上限{ l, l' }及び、下限{l, l'}が存在することである。

　　・束の最小元　φ=Lをボトムと言い、記号⊥で表す：⊥=φ=L

　　・束の最大元　φ=Lをトップと言い、記号Τで表す：Τ=φ=L

　したがって、束は (L,,,,⊥,Τ)により規定される。

　l, l'とそれらの上限、下限を図示すると、次のような菱形になる。この菱形が繰り返されることにより、

束はラティス状になる。

　　　　　　　　　　　　　　図１．２　上限と下限

　束の例は（２）完備束の例を参照。　束でない半順序の例は下記；

　　L={a, b, c, d, e, f }に関係ef, ad, ce, de, ac, ebが成り立つとする。

　　これをハッセ図で表すと下記となる；

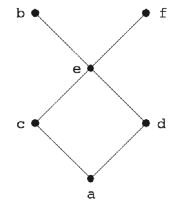
　　　　図１．３　束でない半順序の例

　これは半順序であるが束ではない。その理由は、{ b, f }が存在しないからである。

（２）完備束(Complete Lattice)

　半順序集合(L,)が完備束であるとは、任意の部分集合KLに対して、Lの中にその上限K及び、下限Kが存在することである。束と同様、完備束は(L,,,,⊥,Τ)により規定される。

[例１] 実数の閉区間 [0, 1]は≦の順序の下で完備束であるが、半開区間 [0, 1)は完備束ではない。

　　　理由：１に収束する[0, 1)内の任意の無限列が上限を持たないため。

[例２] 区間の作る束

　Zを整数の集合とするとき、Z上の区間の束（Interval,⊆)は以下のように記述され、完備束となる；

　Interval = {⊥}∪{ [z₁, z₂] | z₁≦z₂,　z₁∈Z∪{-∞},　z₂∈Z∪{∞} }

ここでZの順序≦は、-∞≦z,　z≦∞、-∞≦∞と設定することにより、Z'=Z∪{-∞,∞}上の順序に拡張される。⊥は空(empty)の区間で[z₁, z₂]は区間の端点を含むz₁からz₂への区間である。

Intervalの要素をintで表すことにする。

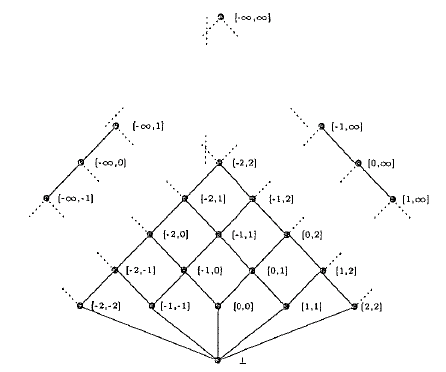
　　　　　　　　　　図１．４　完備束Interval =（Interval,⊆)

（３）不動点(Fixed Points)

　完備束上の単調関数に対しては、有名なタルスキの不動点定理が成立する。この定理は第３章でしばしば使用するのでここで説明する。

■半順序集合(L,)から(L,)への関数f:L→Lが単調関数(monotone function)であるとは、

　任意のl, l'∈Lに対して、ll'ならばf(l)f(l')となることである。

　いま、完備束(L,,,,⊥,Τ)上の単調関数f:L→Lを考える。fの不動点（注）とは、f(l)=lとなるようなLの要素であり、そのような不動点の集合をFix(l)={ l | f(l)=l }と書くことにする。

　　　　（注）数学において写像の不動点とは、その写像によって自分自身に写される点のことである。

　　　　　　　xが写像fの不動点であるとは、f(x)=xが成り立つときに言い、かつそのときに限る。

　Lは完備束なので、完備束の定義から集合Fix(l)がLで下限、上限を持つことが分かる。それらを各々

lfp(f), gfp(f)とすると、下限、上限の定義から

　　　　　　　　　lfp(f)=Fix(l), gfp(f)=Fix(l)

となる。ここで、問題となるのは、lfp(f), gfp(f)もまたfの不動点になるかということである（不動点の極限が不動点になることは自明ではないので）。これに答えるのが次のタルスキの不動点定理である。

■（タルスキの不動点定理）

　(L,,,,⊥,Τ)を完備束とするとき、f:L→Lが単調関数ならば、lfp(f)とgfp(f)は下記を満たす；

　　　　　　　lfp(f)∈Fix(l), gfp(f)∈Fix(l)

　すなわち、最小の不動点と最大の不動点が存在する。

[証明]　まず、準備として次のような縮小と拡大の関数を定義する；

　　関数fは、f(l)lのとき縮小的(reductive)であるといい、そのような縮小点の集合を

　　　　　　　　　　　　　Red(f)={ l | f(l)l }

　　と書く。また、関数fは、l≦f(l)のとき拡大的(extensive)であるといい、そのような拡大点の集合を

　　　　　　　　　　　　　Ext(f)={ l | lf(l) }

　　と書く。

　　Lは完備束なので、完備束の定義から集合Red(f)がLで下限を持つことが分かる。Red(f)の下限を

　　l₀=Red(f)とすると、下限の定義から全てのl∈Red(f)に対してl₀lとなる。fが単調関数なので、

　　l₀lならばf(l₀)f(l)である。一方、l∈Red(f)なのでf(l)lである。したがって、f(l₀)f(l)lより

　　f(l₀)lが導かれる。この式は全てのl∈Red(f)に対して成立するので、f(l₀)はl∈Red(f)の上限を越え

　　ることはない。すなわち、f(l₀)l₀　・・・・(1)

　　一方、fは単調関数なので(1)より、f(f(l₀))f(l₀)　したがって、f(l₀)∈Red(f)となる。l₀はRed(f)の下限

　　なので、l₀f(l₀)　・・・・(2)

　　となる。(1), (2)より、f(l₀)=l₀が得られた。すなわち、　l₀=Red(f)はfの（最小の）不動点であるので、

　　l₀∈Fix(l)となる。また、Fix(l)Red(f)より全てのl∈Fix(l)に対してl₀lである。すなわち、l₀はFix(l)

　　の下限である；l₀= lfp(f)。したがって、lfp(f)はfの最小不動点である。gfpについても同様。(QED)

タルスキの不動点定理の証明に登場するFix(f), Red(f), Ext(f), lfp(f), gfp(f)を図示すると、下の図のような関係になる（この図は抽象解釈でよく使われる）；

　　　　　　　　　　　　　　　　　　　図１．５　fの不動点

■タルスキの不動点定理の簡単な説明図

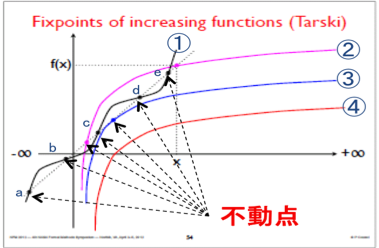
　　　　　　　　　図１．６　単調増加関数の不動点

　　上の図で、①～④は何れも単調増加関数（xの値が増加するとyの値も増加する関数）である。

　図では、

　　・関数①は完備区間R(=-∞≦x≦+∞)上の関数なので常に不動点を持つ。

　　・関数②③④は完備でない区間上(0<x≦+∞)の関数なので不動点を持つとは限らない（④のケース）

　また、①と直線y=xの交点を図のようにa, b, c, d, eとし、そのx座標をa_x, b_x, c_x, d_x, e_xとすると、

　　　　　Fix(f)={ a_x, b_x, c_x, d_x, e_x}、lfp(f)とgfp(f)は各々Fix(f)の下限と上限なのでlfp(f)=a_x、gfp(f)=e_x

　　　　　Red(f)={ x | -∞≦x≦a_x又はb_x≦x≦c_x又はd_x≦x≦e_x}より、Red(f)= a_x

　　　　　Ext(f)= { x | a_x≦x≦b_x又はc_x≦x≦d_x又はe_x≦x≦+∞}より、Ext(f)= e_x

１．２　再帰と不動点

１．２．１　再帰(recursion)とは？

　・式のなかで自分自身を呼び出すことを再帰呼び出しといい、そのような式を再帰式という。

　　・・・プログラムの場合は再帰プログラムといわれる。

１．２．２　簡単な再帰式の例

[例１]下記は左辺のXが右辺のXにより定義されている（循環定義）ので再帰式である；

　　　　　　　X＝X/2 + 1　・・・・①

　この式は非常に単純なのでXの一次方程式と見ればすぐに解ける（X=2)

　しかし、①を再帰式と見て解いてみると、「再帰と不動点の世界」が見えてくる。すなわち、

　　　　　　　X＝X/2 + 1　・・・・①

　まず、①を漸化式で表現する；

　　　　　　　X_n+1=X_n/2 + 1・・・②

　②をX₀=0から出発して順次値を求めていくと、

　　　　　　　X₀=0, X₁=X₀/2+1=1, X₂=X₁/2+1=1/2+1=3/2=1.5, X₃=X₂/2+1=3/4+1=7/4=1.75,

　　　　　　　　X₄=X₃/2+1=7/8+1=15/8=1.875, X₅=X₄/2+1=15/16+1=31/16=1.9375,・・・・

　このように、X₀, X₁, X₂,・・・の値は単調増加し、２に収束していく。

　①の右辺をXの関数とみて、F(X)=X/2+1・・・③

　とすると、①はX=F(X)を満たすXを求めること、すなわちFの不動点を求めることと同じである。

　②の漸化式による収束計算でFの不動点を求める手順を図で表すと、図１．７のようになる。

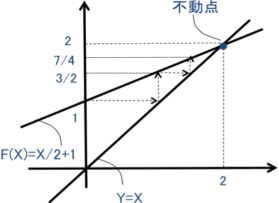
　　　　　　　　　　　　図１．７　不動点を求める手順の図示

　　図２において、不動点Xはまた、Fの出発点の値の極限としても求まる；

　　X₁=F(X₀)=1, X₂=F(X₁)=F(F(X₀))=F²(X₀)=3/2, X₃=F(X₂)=F(F(X₁))=F³(X₀)=7/4,

　　X₄=F(X₃)=F(F(X₂))=F⁴(X₀)=15/8,・・・・, X_n=F(X_n-1)=Fⁿ(X₀)=(1+2+2²+・・・+2^(n-1))/2ⁿ+1=2-1/2ⁿ

　　より、X=lim Fⁿ(X₀)=2　(n→∞）

上の例から、再帰と不動点は密接な関係があることが分かる。

[例２] 例１では、変数が1個の単純な再帰式を扱った； X＝X/2 + 1　

　しかし、再帰式が扱う対象は変数でなくもっと一般的に関数でもよい（注）。この場合の簡単な例を2番目の例とする。

　　　（注）但し、常に変動する関数（例：f(x)=(-1)^[x]）など扱えない関数もある。

　f(x)=x²+1として、再帰式　f(x)=f(x)/2 + 1・・・④

　を考える。　

　その１の例と同様に、まず、④を漸化式で表現する；

　　　　　　　f_n+1(x)=f_n(x)/2 + 1・・・⑤

　⑤をf₀(x)=0から出発して順次値を求めていくと、

　　　　　　　f₀(x)=0, f₁(x)=f₀(x)/2+1=1, f₂(x)=f₁(x)/2+1=1/2+1=3/2=1.5,・・・・

　④の右辺をf(x)の関数とみて、F(f(x))=f(x)/2+1・・・⑥

　とすると、④はf(x)=F(f(x))を満たすf(x)を求めること、すなわちFの不動点を求めることと同じである。

　前と同様にして、f(x)=F(f(x))の不動点は、f(x)=2となるので、f(x)=x²+1=2より、x=±1が求まる。

　以上を纏めると、

　f(x)=x²+1として、再帰式　f(x)=f(x)/2 + 1を考えたとき、

　　　・「f(x)=x²+1は再帰式の部分式（関数）」であり、

　　　・「F(f(x))=f(x)/2+1」はf(x)上の汎関数（関数の関数）である。

　従って、再帰式の不動点は「再帰式の中の部分関数f上の汎関数Fの不動点として捉える」ことである。

１．２．３　階乗を求めるプログラム　　

　ここでは、再帰プログラムと不動点の例としてよく知られている「階乗を求めるプログラム」を考える。

　整数を入力し整数を出力するプログラム

　　　　　　　f(x) = if x=0 then 1 else x*f(x-1)　　　　・・・(1)

は、典型的な再帰プログラムである。このプログラムは非負整数の入力についてその階乗を出力する。

ここで、次のように定義された汎関数Fを考える；

　　　　　　　x=0のとき、F(f(x))=1,

　　　　　　　x≠0かつf(x-1)が定義されているとき　F(f(x))=x*f(x-1)　・・・(2)

　　　　　　　但し、x=0, 1, 2, 3,・・・（0及び正の整数）

上記の定義から次のことが分かる；

　・関数fは(2)式の一部を構成しているので、(2)式の部分関数である。

　・(2)式のF(f(x))=x*f(x-1)は、左辺の関数fが右辺の関数fにより再帰的に定義されている。

　・Fは関数fを変数とする（汎）関数（関数の関数）である。

このとき、再帰プログラム(1)の表す関数fは、汎関数Fの不動点として特徴付けられることを以下に示す。まず、(2)式を漸化式により解いてみる；

　・(2)の部分関数fの出発点は空関数f(x)=φ(x)とする。すなわち、任意の変数xに対して未定義となる

　　関数とする；φ(x)=undef（未定義）

　・（汎）関数F(x)をk回代入した関数をF^k(x)=F(F(...(F(x))と表す。

　・以下、φ(x)=undef（未定義）から出発して、順次(2)の漸化式を解いていく；

　　　k=0の場合：F⁰(φ(x))=φ(x)=undef（←F(x)を0回代入するとはxそのもの）

　　　k=1の場合：Fの定義からx=0のとき、F¹(φ(x))=F(φ(x))=1、x≧1のときF¹(φ(x))=x*φ(x-1)=undef

　　　k=2の場合：x=0のとき、F²(φ(x))=F(F(φ(x))=1、→F(f(0))=1なのでF(1)=1であることが分かる。

　　　　　　　　　　　　　x=1のとき、F²(φ(x))=F(F(φ(x))=x*F(φ(x-1))=1*F(φ(0))=1*1=1

　　　　　　　　　　 x≧2のとき、F²(φ(x))=F(F(φ(x)) =x*F(φ(x-1))=x*((x-1)*φ(x-2))=undef

　　　k=3の場合：x=0のとき、F³(φ(x))=F(F²(φ(x))=F(1)=1、

　　　　　　　　　　x=1のとき、F³(φ(x))=x* F²(φ(x-1))=x*F(F(φ(x-1)))=1*F(F(φ(0))=1*F(1)=1*1=1、

　　　　　　　　　　　　　x=2のとき、F³(φ(x))= x* F²(φ(x-1))=x*((x-1)*F(φ(x-2))=2*1*1=2!

　　　　　　　　　　　　　x≧3のとき、F³(φ(x))= undef　（←F³(φ(x))= x* F²(φ(x-1))=x*((x-1)*F(φ(x-2))

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　= x*((x-1)*(x-2)*F(φ(x-3))=undef）

　　　k=4の場合：x=0のとき、F⁴(φ(x))=F(F³(φ(x))=1、

　　　　　　　　　　　　　x=1のとき、F⁴(φ(x))=x* F³(φ(x-1))=x*F(F²(φ(x-1)))=1*F(1)=1*1=1、

　　　　　　　　　　　　　x=2のとき、F⁴(φ(x))= x* F³(φ(x-1))=x*((x-1)*F²(φ(x-2))= x*((x-1)*F(F(φ(x-2)))

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　=2*1*F(1)=2*1*1=2!

　　　　　　　　　　　　　x=3のとき、F⁴(φ(x))= x* F³(φ(x-1))=x*((x-1)*F²(φ(x-2))

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　= x*((x-1)*(x-2)*F(φ(x-3))=3*2*1*1=3!

　　　　　　　　　　　　　x≧4のとき、F⁴(φ(x))= undef

　　　　　　　　　　　　　⇒k=4の場合を纏めると、F⁴(φ(x))=x! (0≦x＜4)、　F⁴(φ(x))= undef (x≧4)

　　　同様にして、下記が成立する；

　　　　k=nの場合：Fⁿ(φ(x))=x! (0≦x＜n)、Fⁿ(φ(x))= undef (x≧n)

　ここで、F⁰(φ(x)), F¹(φ(x)), F²(φ(x)),・・・, Fⁿ(φ(x)),・・・の関係がとうなるかを考えてみる（ここでの

　話は、横内寛文著「プログラム意味論」のP.75～P.77及びP.63,64,71より）；

　任意のxに対して、

　　　F⁰(φ(x))=undef⊆ F¹(φ(x))={1, undef}⊆ F²(φ(x))={1, undef}⊆ F³(φ(x))={1, 2!, undef}

　　　⊆ F⁴(φ(x))={1, 2!, 3!, undef}⊆ ・・・ ⊆ Fⁿ(φ(x))={1, 2!, 3!,・・・, (n-1)!, undef}・・・

　すなわち、F⁰(φ(x)), F¹(φ(x)), F²(φ(x)),・・・, Fⁿ(φ(x)),・・・は単調増大である；

　　　F⁰(φ(x))⊆F¹(φ(x))⊆F²(φ(x))⊆・・・⊆Fⁿ(φ(x))⊆・・・　(3)

　ここで、(3)式の上限をF^*(φ(x))とすると、

　　　F^*(φ(x))={ Fⁿ(φ(x))| n∈N}=∩{ l∈N |任意のl'∈Fⁿ(φ(x))に対し、l'⊆l }=x!

　なので、F^*(φ(x))=x!

　したがって、x≠0のとき、(2)式よりF(F^*(φ(x)))=x* F^*(φ(x-1))=x*(x-1)!=x!= F*(φ(x))となり、

　F^*(φ(x))=x!はFの不動点となる。

１．３　ガロア接続

　ガロア接続は抽象解釈やモデル検査で対象の複雑さを単純化させる対応関係として使用される。名前の通り、この概念の起源はガロア理論にある。これに関しては付録IIを参照。

１．３．１　ガロア接続の概念

　まず、直感的に「ガロア接続」を説明すると、

　・ガロア接続は、「一方の世界(C)についての情報」を、「もう一方の世界(A)」に渡すことを実現するため

　　に、２つの”世界”をお互いに関係付ける。

　　すなわち、Ｃの世界で問題を解く代わりに、Ａの世界で問題を解くことができるような対応関係。

　　（Ａの方がＣより問題解決が容易な場合に有効）　もう少し正確に言えば、ある順序構造を（一方の

　　世界から他方の世界へ）保存するように情報の受渡しが行なわれる。

１．３．２　ガロア接続の定義

　　　　L=(L,), M=(M,)を完備束とするとき、

　　　　α：L→Mとγ：M→Lの組み(α、γ）がガロア接続である

　　　　とは、下記を満たすことである（図１．８）；

　　　　任意のl∈ Lとm∈ Mに対し、　α(l)m　⇔　lγ(m)　・・・(1)

　　このとき、Lを具体ドメイン、Mを抽象ドメイン、αを抽象化関数（又は抽象化写像）、γを具体化関数（又は具体化写像）という（このことの意味は次の頁で説明する）。

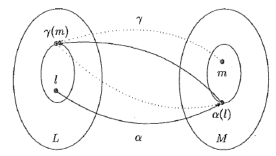
　　　　　　　　　　　　　　　　　図１．８　ガロア接続

１．３．３　ガロア接続の定義の他の表現

　L=(L,), M=(M,)を完備束とするとき、（α、γ）がガロア接続であることと、下記は同値である；

　　α：L→Mとγ：M→Lが単調関数で、l∈L, m∈Mとするとき

　　下記の式を満たす；

　　　　　　　　lγ○α(l)　　　・・・・(2-1)

　　　　　　　　α○γ(m)m　・・・・(2-2)

　（証明）最初に、他の表現⇒ガロア接続を示す；

　　α(l)mとすると、γは単調なのでγ(α(l) )γ( m )。lγ○α(l)を使用すると、　lγ(m)

　が得られる。同様にlγ(m)とすると、α(l)mが得られる。

　したがって、他の表現⇒ガロア接続が示された。

　次に、L=(L,), M=(M,)を完備束、α：L→Mとγ：M→Lの組み(α、γ）がガロア接続とし、

　これが他の表現となることを示す。まず最初に、lγ○α(l)を示す；

　任意のl∈ Lに対してα(l)α(l)であるので、α(l)m→ lγ(m)においてm=α(l)と

　置くと、lγ(α(l))が得られる。α○γ(m)mについても同様に示すことができる。

　次に、αとγが単調であることを示す。l₁l₂とすると、lγ○α(l)はすでに示されているので

　　l₁l₂γ(α(l₂))となる。lγ(m)　→　α(l)mなので、l₁γ(α(l₂))→α(l₁)α(l₂)となり、

　αは単調増加となる。γについても同様に示すことができる。

■ガロア接続の意味すること

　・条件(2-1)について：この式は、「l∈Lをαで移したものα(l)はγでLの世界に戻すと、lより広く

　　なるので、α(l)にはlに属さないものもαで移されている」ことを示している。すなわち、α(l)はlより

　　広い範囲を示しているが、どんな場合でも元のlの値は確実に表現されている。したがって、α(l)は

　　lの近似である。この意味からαは抽象化関数と言われる。

　　　　　　　　　図１．９　条件(2-1)の図示

　・条件(2-2)について：この式は、「m∈Mをγで移したものγ(m)はαでMの世界に戻すと、mより狭く

　　なるので、γ(m)は確実にMにおいてmで近似できるLの要素の集合である」ことを示している。

　　　　　　　　　図１．１０　条件(2-2)の図示

■ガロア接続の簡単な例１

　　具体ドメインLを整数全体の集合Z、抽象ドメインMをZ上の区間の束（Interval)とするとき、

　　抽象化と具体化の関数α、γは次のように定義され、ガロア接続となる；

　　　　　　α(I)=[min I, max I]、α(空集合）=⊥

　　　　　　　γ（[ l, u ])={x∈Z | l≦x≦ u }、γ(⊥)=空集合

　　抽象ドメインMは、下限がlで上限がuである区間の集合で、直感的には、lとuの間の値を

　　抜き取ったものである。この区間は具体化関数γによりlとuの間の値を埋めたものとなる。

■ガロア接続の簡単な例２

　　二次元の簡単な例としては、P. Cousot, "An Inmormal Overview of Abstract Interpretation"に

　次の例がある；

　①具体世界Cの任意の部分集合ciから、2次元の区間（区間の両端の値のみでその間の値を抜き

　　取ったもの）からなる抽象世界Aへの写像αを「抽象化写像」という。

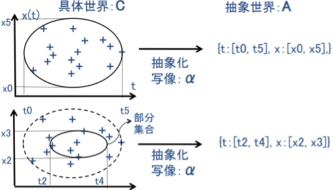
　　　　　　　　　図１．１１　抽象化写像の例

　②逆に、2次元の区間からなる抽象世界Aから具体世界Cの部分集合への写像γを「具体化写像」

　　という。この例では、具体化写像は2次元の区間と矩形を対応させている。

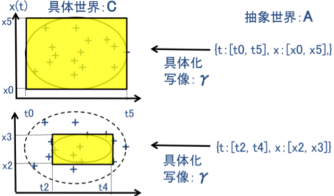
　　　　　　　　　図１．１２　具体化写像の例

１．３．４　ガロア接続の性質

　(L,α,γ,M)がガロア接続ならば、

　αはγ(m) =∪ { l |α(l)m }によりγを一意に決定し、

　 γはα(l) =∩ { m | lγ(m) }によりαを一意に決定する（注）。

　　　　（注）γ(m) = max { l |α(l)m },α(l) = min { m | lγ(m) }とも表現できる。

　【証明】　

　　　ガロア接続の定義より、

　　　　γ(m) =∪ { l | lγ(m)} =∪ { l |α(l)m }　　

　　　これはαがγを決定していることを示している。

　　　次に一意に決定していることを示すために(L,α,γ₁,M)と(L,α,γ₂,M)をガロア接続とすると、

　　　γ₁(m) =∪ { l |α(l)m }=γ₂(m)なのでγ₁=γ₂となる。

　　　同様に、α(l) =∩ { m |α(l)m }∩ { m | lγ(m) }であり、これはγがαにより一意に決定

　　　　されることを示している。(Q.E.D)

１．３．５　ガロア挿入

　(L,α,γ,M)が完備束(L,）と(M,）間のガロア挿入(Galois Insertions)であるとは、

　α：L→Mとγ：M→Lが単調関数で下記を満たすことである（図１．１３）；

　　　　　　　　　　　　　　lγ○α(l)　

　　　　　　　　　　　　　　α○γ(m)= m　　←ここが等式！

　　このように、ガロア挿入は、最初に具体化、次に抽象化を行うことに対して正確さを失わない。その

　結果、MはLの要素を記述しないような要素は含まない。

　すなわち、Mは偽反例（注）となる要素を含まない。

　　（注）抽象化の世界Mで否定される性質(xがmに属さない)が具体構造では否定されない場合、「偽反例」という。

　　　　　ガロア挿入の場合、α○γ(m)= mなのでxがmに属さないならばγ(x)はγ(m)に属さない。

　　　　　（もし、γ(x)∈γ(m)ならば、α○γ(x)= x∈α○γ(m)= mとなり矛盾）。したがって、Mに偽反例はない。

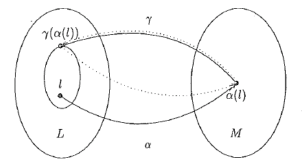
　　　　　　　　　　　　　図１．１３　ガロア挿入