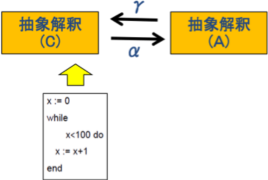
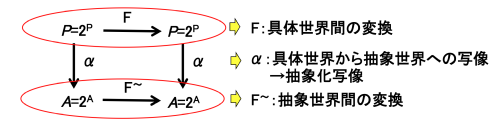
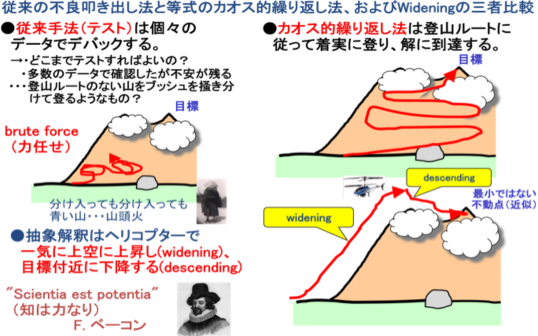
æQÍ@ÛðßTviåÉCousotú_¶©çj@@@@@@@
QDP@vOÌZ}eBNXiÓ¡_jÆÛðßÌî{pê@@@@@@@@@@@@@@
@±±ÅÍAvOÌÛðßðtH[}Éè`·é½ßÉÖW·évOÌZ}eBNXÆÛðßÅp¢çêéî{Ipê(*)ðÈPÉÐî·éBi±ÌßÍCousotú_¶ÌRßASßÉY·éj@@
(*)m[hâ«AóÔÈÇÌpêÍAScott and StracheyÌ"Mathematical semantics of Program"(1971)Åè`³êÄ¢éB
@ܸAõƵÄvOÌZ}eBNXÉ¢ÄྷéB
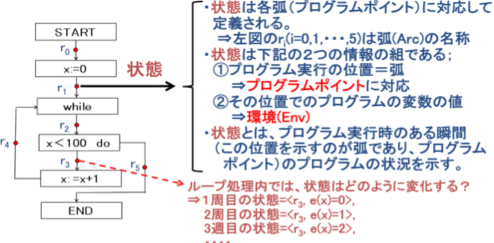
¡vOÌZ}eBNXiÓ¡_jÆÍH
@vOPÌZ}eBNXÆÍA»ÌvOð]¿µ½¢ÚÉ ÚµÄA»êÌÂ\ÈÀsð
Lq·éuvZfvÅ éBµ½ªÁÄA»±ÅÍvOÌ]¿ÎÛÉÖWÌÈ¢ÚÍÌ
³êéBvOÌZ}eBNXðLq·éû@ͽ éªA±±ÅÍvZXebvPÊÉ»Ì
óÔÌÏ»ðLq·ég[Xx[XÌìIZ}eBNX(operatinal semantics)ðl¦éB
¡g[Xx[XÌìIZ}eBNXá
@D. Schmidt, All the World is an abstract interpretationÉÚÁÄ¢éÈPÈáðºLɦ·G
@@@@@@@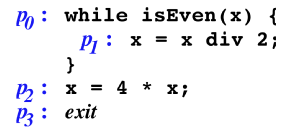
@@@@@@@@ip0, p1, p2, p3ÍvOisÌÊuð¦·vO|Cgj
ãLÌvOÌìIZ}eBNXÍAºLÌ4ÂÌJÚ[ðgpµÄvO|CgÆÏÌlÌgpp, xðXV·éG
@@@@@
±ÌÆ«AãLÌvOÌìIZ}eBNXͺLÌg[XƵÄ\³êéG
vOÌÏxÌlª12ƵÄ^¦çê½Æ·éÆA
@@@@@@@![]()
ip0,12Éæèx=12A p1,12Éæèx=6A p0,6Éæèx=6Ap1,6Éæèx=3Ap0,3Éæèx=3Ap2,3Éæèx=12æèp3,12)
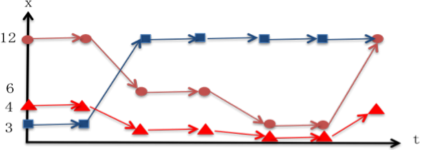
±êðA¡²ÉÔÌoßÉæévO|CgÌÏ»Ac²ÉÏÌlðæèAOtÅ\·ÆA
ºÌ}Ìæ¤É\»Å«éG
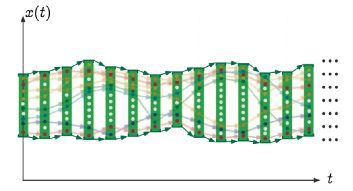
@@@@@@@@@@
@@@@@@@@@@@}QDP@ìIZ}eBNXÌg[XÌOt
ãLÌvOÅÏÌúlÌ^¦ûðϦéÆÙÈég[Xª¾çêéBá¦ÎA
@@@x=3ÌÆ«Ap0,3¨p2,3¨p3,12
@@@x=4ÌÆ«Ap0,4¨p1,4¨p0,2¨p1,2¨p0,1¨p2,1¨p3,4
@@@@@
@@@@@@@}QDQ@ìIZ}eBNXÌÂ\Èg[XiêªjÌOt
@±Ìæ¤ÉAZ}eBNXÍSÄÌÂ\ÈÀs«ÅÌvOÌÀsðÓ¡·éÌÅAg[Xx[XÌìIZ}eBNXÍÔtÌÖƵÄvOÌÏÌlÈÇÌxNgx(t)ÌÏ»ð¦·J[uƵĺLÌæ¤É\»³êéG
@@@@@@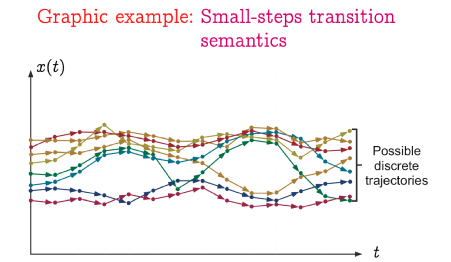
@@@@@@@@@@}QDR@Â\Èg[XÌOt\»á
È~AìIZ}eBNXðè`·é½ßɺLÌpêÉ¢ÄÈPÈáÉæèྷéG
@@@@EvOÌm[h(Node)ÆÊ(Arc)yÑvO|Cg
@@@@Em[hÌ^CviJnAãüAÚAªòAoûj
@@@@E«(Encironment)
@@@@EóÔ(State)
@@@@EReLXg(Context)
@@@@EReLXgxNg(Context-Vector)
@@@@En-ReLXg(n-context)
@@@@EF-contÖ
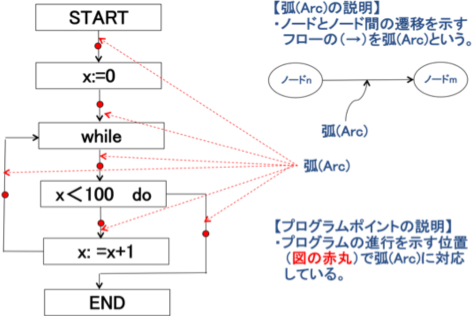
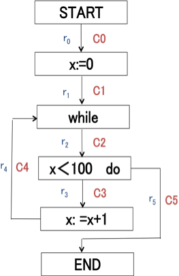
iPjm[hÆ»Ì^Cv
@@@vOÌm[hÍ}QDSÌæ¤ÉAJnAãüAÚAªòAoûÌem[hª éBeXÌ
@@Ó¡ÍA}ÌEÌm[hÌà¾ðQÆB
@@@@
@@@@@@}QDS@vOÌm[h
¡ãüm[hÉ¢ÄÌâ«à¾Fãüm[hnÍA»Ìm[hnÅuE¤Ì®expr(n)Ìlð¶¤Ì
@¯Êqid(n)Éãü·éB·Èí¿Aid(n) = expr(n)@iãÌáx:=x+1ÅÍAid=x, expr=x+1j
@ ±±ÅA¯ÊqÆÍAÏA豫AÖ̼OÅ éB¯ÊqÌSÌÍIdentÅ\·B
iQjÊ(arc)ÆvO|Cg
@@m[hÔÌJÚÆvOÌisÊu𦷽ßÉÊÆvO|Cgª éB}QDTðQÆB
@@@
@@@@@@@@}QDT@ÊÆvO|Cg
@ÈãÍvOÌ\¢É¢ÄÌî{IÈpêÅ éBÉAvOÓ¡_ÅgíêépêÅ éu«vÆuóÔvÉ¢ÄྷéB
iRj«(Environment)
@@«ͯÊqiÏA豫AÖ̼OjÆ»ÌlðÑt¯éàÌB·Èí¿A«ͯÊq
@©çlÌæÖÌÖÌSÌÅ éF@@Env = Ident¨ Values@iValuesÍlÌWj
@µ©µA±±ÅͯÊqƵÄuÏvÉÌÝ ÚµÄl¦éB·Èí¿AuAn environment(Env) is a
@valuation for each variable of the programvÅ éÆ·éBÈPɾ¦ÎAu«ÆÍAÏÆ»ÌlÌ
@ÎBÏÌgðè`·éàÌvÅ éBºÌ}ðQÆB
@@@@@@
@@@@@@@@@@@@@}QDU@«Ìà¾
@iájeðÏx, yÉ5, 10ðγ¹é«ƷéB ±êðeox¨5, y¨10pƱÆà éBÓ¡
@@@Íe(x)=5, e(y)=10Ư¶B¨È~ÍAe(x)=aÌ\LðgpBÓ¡_ÅÍe(x)=[[x]](e)ÆàB
iSjóÔ(State)
@@óÔStateÍ<Arc, Env>ÌgÅ èAvOÀsÌ évO|CgÅÌvOÌóÔð¦·iStates = Arcs~EnvjB¨}QDVðQÆB
@@@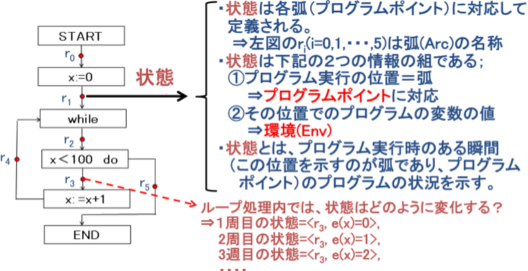
@@@@@@@}QDV@óÔÌà¾
¡óÔ<Arc, Env>ÌÈPÈÏ»áð}QDWɦ·B
@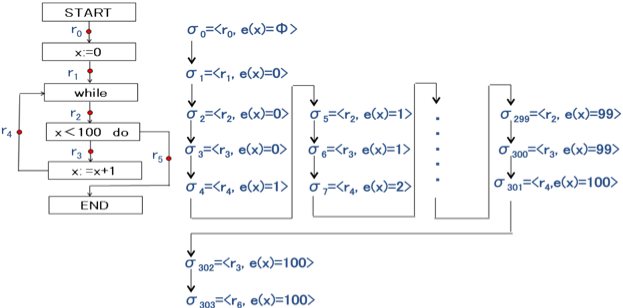
@@@@@@@}QDW@óÔÌÏ»á
ãLÌvOÌìIZ}eBNXͺLÌg[XƵÄ\³êéG
@@@@Ð0¨Ð1¨Ð2¨ EEEEE ¨Ð303
vOÌóÔÍAúóÔ©çoµÄA^¦çê½óÔs=<a, e>ÌuÌóÔ(next state)vð
¦·Ön-state(State<a, e>)©çìé±ÆªÅ«éG
EI-StatesÍúóÔÌWÅ éBvOÌ«¿ÍevO|CgÉÖWµ½hóÔÌ
@@WhðgpµÄ²×çêéBI-StatesÍÌæ¤Éè`³êéG
@@@@@@I-States = { <üûm[hÌã±ÌÊ ,{gÌEnv >}
@@}QDWÌáÅÍAI-States=<r0, e(x)=Ó}>=Ð0Å éB
@E^¦çê½óÔs=<a, e>ÌuÌóÔ(next state)vð¦·Ön-state(State<a, e>)Í_¶Ì
@ASYðQÆBn-stateÖÉæè}QDWÌóÔð\»·éÆA
@@@Ð0=I-States,Ð1=n-state(Ð0),Ð2=n-state(Ð1)=n-state(n-state(Ð0))=n-state2(Ð0),
@@@Ð3=n-state(Ð2)=n-state(n-state2(Ð0))=n-state3(Ð0),EEEEÐn= n-staten(Ð0)
@@@¡An-state0ðPÖÆ·éÆAn=0,1,2,EEEÉεÄAÐn= n-staten(Ð0)ÆÈéB
@@@·Èí¿ACÓÌóÔÍúóÔÆn-stateÖ©çìé±ÆªÅ«éB
@@@±±ÅAivOªû©µjÅIóÔª éƵÄA±êðn-stateÆ·éÆA
@@@n-state= n-state(n-state(EEE(Ð0))EE)Å éB
@@@±êÍAóÔsÆÌóÔðγ¹éÖF(s)=n-state(s)ÌŬs®_Å éB
@@@·Èí¿An-state=F(n-state)@@iFÍÄÖj
@[ÅßÌ_¶©çÌß]
@2000NÌP. CousotÌ_¶uÛðßF»ÌB¬ÆW]vi¶£ÌNO.POjÅÍAvOÌìIZ}eBNXÉæèAg[XÐ0¨Ð1¨Ð2¨ EEEEE ¨Ð303ðßé±ÆðA
u±Ìg[XÉÁÄ»êéóÔÌWÉæég[XÌÛÅ éF¿S(Ð)={ÐkF k¸[0, |Ð|]}v
Æl¦Ä¢éBµ½ªÁÄA}QDWÌáÍA|Ð|=303ÈÌÅ
¿S(Ð) = {Ðk F k¸[0, |Ð|]}={Ðk F k¸[0, 303]} = {Ð0,Ð1,Ð2,EEE,Ð302,Ð303 }ÆÈéB
@ÉAvOÌÏÌ©_ðWJ·é½ßÉ
@@@@EReLXg(Context)
@@@@EReLXgxNg(Context-Vector)
@@@@En-ReLXg(n-context)Ö
@@@@EF-contÖ
@Æ¢¤TOªoê·éB
iTjReLXg(Context)
@@±êÍSÄÌÂ\È«ÌWÅ èAvO|Cgi·Èí¿AÊ(Arc)jÉt¯çêÄ¢é;
@@@Context = 2Env@@@iReLXgÍ«EnvÌxLWj
@t[ÌáÅÍAEnv={e(x)=0, e(x)=1, e(x)=2,EEE(,e(x)=100)}ÈÌÅA
@@@@ContextÍAEnv={e(x)=0, e(x)=1, e(x)=2,EEE(,e(x)=100)}ÌSÄ̪WÌW
¡ReLXgCq
@@ReLXgCqÆÍvO|Cgq(¸Arcs)ÅÌReLXg̱ÆÅ éB
@·Èí¿AvOÌÂ\ÈvZV[PXɨ¢ÄqÉÖW·éSÄÌ«ÌWÅ èAºL
@Ì®Å\³êéG
@@@Cq={ e | <q, e>=n-statesn(i)ÆÈén0Æi¸I-Statesª¶Ý·é}
@±êÍqðÅèµÄãLÌ®ð½·nª¶Ý·êÎæ¢ÌÅA<q, e>=n-states(Ð0), n-states2(Ð0),
@n-states3(Ð0),EEE, n-statesn(Ð0)ÌóÔÉηé«eÌWÆÈéB
@iájáÌvOÅÍA
@@@@Eq=r1ÌÆ«ACr1={e(x)=³}
@@@@Eq=r4ÌÆ«A
@@@@Cr4ÍA{ e(x)=1,@@@@@©in=4,·Èí¿n-states4(Ð0),Ð0¸I-StateÌêj
@@@@@@@@@e(x)=2,@@@@@©in=7,·Èí¿n-states7(Ð0)Ìêj
@@@@@@@@@e(x)=3 ,@@@@@@©in=10,·Èí¿n-states10(Ð0)Ìêj
@@@@@@@@@EEE }ͱê̪W
@@@@@Ë}QDWÌóÔÌÏ»áÆÎä·éƪ©èÕ¢B
@iUjReLXgxNg(Context-Vector) (Cv)
@@±êÍevO|Cgq¸ArcsÉReLXgðÖW³¹éxNgÅ èAºLÌ®Åè`
@³êéG@ReLXgxNgCv= (Cv(r0),Cv(r1),Cv(r2),EEE,Cv(q),EEEj
@@@@@@@@@@@@@@@@@@@@@= (Cr0, Cr1, Cr2,EEE,Cq,EEEj
@@@@@±±ÅACv(q)={ e | <q, e>=n-statesn(i)ÆÈén0Æi¸I-Statesª¶Ý·é}(=Cq)
@@@@@@i@CviqjÍAReLXgxNgCvÌæq¬ªj
@Cv(q)ÍevO|CgqÅÇIÉè`³êéB
@}QDSÌáÅÍAºLÌæ¤ÈxNgÆÈéi}QDWÌóÔÌÏ»áÆÎä·éƪ©èÕ¢jG
@@@@@Cv= (Cv(r0),Cv(r1),Cv(r2),Cv(r3),Cv(r4),Cv(r5)j
@@@@@±±ÅA
@@@@@@Cv(r0)={e(x)=Ó},Cv(r1)={e(x)=0}
@@@@@@@Cv(r2)={e(x)=0, e(x)=1, e(x)=2,EEE, e(x)=99, e(x)=100}ͱê̪W,
@@@@@@@Cv(r3)={e(x)=0, e(x)=1, e(x)=2,EEE, e(x)=99}ͱê̪W,
@@@@@@@Cv(r4)={e(x)=1, e(x)=2,EEE, e(x)=99}ͱê̪W,
@@@@@@@Cv(r5)={e(x)=100}
@@@@@ÆÈéB
@@¡ReLXgxNgÌvfÌÏ»á
@@@ReLXgxNgCvÌvfÌÏ»ð}QDXÉ}¦µÄÝéReLXgxNgCvÌvfÍ
@@[v̪Žü·é©ÉæèÏ»·é±ÆÉÓB
@@@@@@
@@@@@@@@@@@}QDX@ReLXgxNgÌvfir=riÅÌReLXgjÌÏ»á
@±±ÅAãLÌà¾Ìuͱê̪WvÆ¢¤Ó¡ÍAReLXgxNgª[vÌ
ªÅÍA[vÌñÉæèÊrÉεÄÙÈéReLXgiªWjÆÈé±ÆðwµÄ¢éB
¨±Ì±ÆÍA[vÌñÉæèReLXgxNgÍ¡¶ÝµïÜÖWÉ é±Æð¦µÄ¢éB
@á¦ÎACv1ð[vPñÚÌReLXgxNgACv2ð[v2ñÚÌReLXgxNgÆ·éÆA}QDXÅÍA
@@Cv1=(Cv(r0),Cv(r1),[vPñÚÌCv(r2),[vPñÚÌCv(r3),[vPñÚÌCv(r4),Cv(r5)j
@@@@=({e(x)=Ó}, {e(x)=0}, {e(x)=0}, {e(x)=0}, {e(x)=1}, {e(x)=Ó})@©xNgÌÀÑÍÊriÌÔ(i=0,1,2,3,4,5)
@@Cv2=(Cv(r0),Cv(r1),[v2ñÚÌCv(r2),[v2ñÚÌCv(r3),[v2ñÚÌCv(r4),Cv(r5)j
@@@@=({e(x)=Ó}, {e(x)=0}, {e(x)=0, e(x)=1}, {e(x)=0, e(x)=1}, {e(x)=1, e(x)=2}, {e(x)=Ó})
@ÆÈèACÓÌr=r1,r2,r3,r4,r5ÉεÄACv1(r)ºCv2(r)ÆÈéB
@µ½ªÁÄAReLXgxNgÌWͺL̼º`Æa¾`ð±ü·é±ÆÉæè©ÉÈéG
@@@Cvi, CvjðQÂÌReLXgxNgÆ·éÆ«A
@@@@ECÓÌr¸ArcsÉεÄA(Cviº`Cvj)(r)ðCvi(r)ºCvj(r)Æ·é±ÆÉæèReLXgxNgÌ
@@@@ ¼Cviº`Cvjðè`·éB
@@@@ECÓÌr¸ArcsÉεÄA(Cvi¾`Cvj)(r)=Cvi(r)¾Cvj(r)ÉæèReLXgxNgÔÌ
@@@@ aðè`·éB
@@@@[ؾ]@º`ͼŠéG
@@@@@@@@(i)CÓÌr¸ArcsÉεÄACvi(r)ºCvi(r)ÈÌÅCviº`CviÅ éB
@@@@@@@@(ii)Cviº`Cvj©ÂCvjº`CvkÈçÎACÓÌr¸ArcsÉεÄA
@@@@@@@@@Cvi(r)ºCvj(r),Cvj(r)ºCvk(r)ÈÌÅACvi(r)ºCvj(r)ºCvk(r)æèCvi(r)ºCvk(r)
@@@@@@@@@@@@µ½ªÁÄACviº`CvkÆÈéB
@@@@@@@@(iii)Cviº`Cvj©ÂCvjº`CviÈçÎACÓÌr¸ArcsÉεÄA
@@@@@@@@@@@@Cvi(r)ºCvj(r),Cvj(r)ºCvi(r)ÈÌÅACvi(r)=Cvj(r)ÆÈéB
@@@@@@@@@@µ½ªÁÄACvi=CvjÆÈéB
@@@@@@@AReLXgxNgÌW(Cv,º`)Í©Å éG
@@@@@@@@CÓÌr¸ArcsÆACvi,Cvj¸(Cv,º`)ÉεÄA
@@@@@@@@ãÀ¾{Cvi,Cvj}=(Cvi¾`Cvj)(r)=Cvi(r)¾Cvj(r)ª¶Ý·é½ßB
@@@@@@@@ºÀÍ¿{Cvi,Cvj}=Cvi(r)¿Cvj(r)Ål¦êÎæ¢ijB@
@@@@@@@@ijReLXgxNgÌP²Á¾¯ðl¦éÈçκÀÍsvB
@@@@@@@@@@@¾`ÌÝÌæ¤ÉjoinÆmeetÌÇ¿ç©êûµ©KvƵȢ©ð
@@@@@@@@@@@¼©(semi-lattice)Æ¢¤B
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@(Q.E.D)
@ReLXgxNgÍ[vÌñÉæèP²Á·éªAReLXgxNgÌWÌ
gbvT`Æ{gÛ`ÍÌæ¤Éè`³êéG
@@@@@@@@@CÓÌr¸ArcsÉεÄAT`(r)=Env
@@@@@@@@@@@CÓÌr¸ArcsÉεÄAÛ`(r)=Ó
±ÌÆ«AReLXgxNgÌWÉ{ T`,Û`}ðtÁµ½àÌðüßÄReLXgxNgÌW
Æ·éÆACÓÌReLXgxNgCvÉεÄA
@@@@@@@@@@@@@@@@@@@@Û` º`Cvº`T`
±ÌÆ«AReLXgxNgÌCÓÌWÍãÀAºÀðÂÌÅ®õ©ÆÈéB
iVjn-contextÖ
@iTjÅÍvO|CgqÅÌReLXgCqðè`µ½BÈ~ÅÍvO|CgÆÊð¯êµÄAÊrÅÌReLXgCrÆ¢¤¾¢ûð·éB
@vOÌÓ¡©çÊrÅÌReLXgCrÍAÊrÉ(r'ÌI[m[h=rÌn[m[hjÆ¢¤ðÅ×Ú·éÊr'ÌReLXgCr'ÆA»êçÌÊÌÔÌXe[ggÉæèC³³ê½àÌÅÜéi}QDPOQÆjB
@@@@@@@@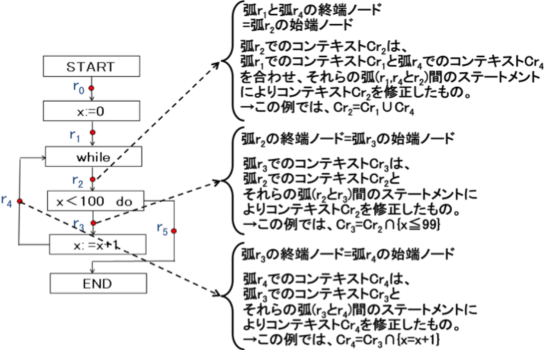
@@@@@@@@@@@}QDPO@ÊrÆ»ÌOÉ×Ú·éÊÌReLXgÆÌÖW
@»±ÅA»ÝÌÊrÅÌReLXgCr=Cv(r)ðAÊrÌJnm[hªI[m[hÆÈé×Úµ½ÊÌReLXgÆA»êçÌÊÌÔÌXe[gg©çßéÖðl¦A»êðn-context (n-ÍnextÌÓ¡jÅè`·éG@
@@@@@@@@@@Cr=Cv(r) = n-context(r, Cv)
·Èí¿An-contextÍuCv(r)ðÌReLXgÆ·évæ¤ÈReLXgÅ\·ÖÅ éB
@@@@@@iáj}QDPOÌáÅÍACr2=Cv(r2)=n-context(r2,Cv)=Cr1¾Cr4
@@@@@@@@@@@@@@@@@@@@@@@@@@@Cr4=Cv(r4)=n-context(r4,Cv)=Cr3¿{x=x+1}
ܽAn-contextÖÍvOÌXe[ggðReLXgɽf·éÌÅAuvOÌî{½ßiXe[ggjÌðßvÆl¦çêéB
ËCousotú_¶Ì5.1ßÅÍA±êÉֵĺLÌLqª éG
@@uThe local interpretation of elementary program constructs which is defined by n-context is used to
@@ associate a system of equations with the program.in-contextÉæèè`³êévOÌÇI
@@@ðßÍvOÌ®ÌVXeÉÖA³¹é½ßÉgp³êéjv
@ReLXgxNgÌWͼº`ƾ`Éæè©ÆÈéªA±±ÅAReLXgxNgCvª^¦çê½Æ«AuCvðÌReLXgxNgÆ·évæ¤ÈReLXgxNgðßéÖðl¦A±êðF-contÆ·éB·Èí¿ACÓÌr¸ArcsÉεA
@@@@@@@F-cont(Cv)(r)=n-context(r,Cv)@ é¢ÍAF-cont(Cv(r))= n-context(r,Cv)
Å éB±ÌÆ«AF-contÍReLXgxNg̼º`ÉÖµÄ۶ŠéG
@@@@@@@Cv1º`Cv2@ÈçÎAF-cont(Cv1)º` F-cont(Cv2)
@@[ؾ]Cv1º`Cv2@ÈçÎACÓÌr¸ArcsÉεA
@@@@@@@@F-cont(Cv1)(r)= n-context(r,Cv1)= Cv1(r)ºCv2(r)=n-context(r,Cv2)= F-cont(Cv2)(r)@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@(Q.E.D)
@ReLXgxNgÌP²ÁñFÛ`º`Cv1º`Cv2º`Cv3º`EEEEɨ¢ÄA
@F-contðl¦éÆAF-contͺ`ÉÖµÄÛ¶ÈÌÅF-contÍ®õ©ãÌP²ÁÖ
ÆÈéBµ½ªÁÄA^XLÌs®_èæèAF-contÍs®_CvðÂGF-cont(Cv) =Cv
@@±ÌCvÍvOÌÏxÌæè¾élÌÅålÆÈèAvO|CgÉ˶µÈ¢
@vOÌåæIÈ«¿Å éijB
@@ijCousotú_¶ÌvñÅÍA±Ì±ÆªºLÌæ¤É©êÄ¢éG
@@@@uThe program global properties are defined as one of the extreme fixpoints of that, Tarski.
@@@@ivOÌO[oÈ«¿Í^XLÌs®_ÌêÂƵÄè`³êéBjv
@[ÅßÌ_¶©çÌß]
@ReLXgÆReLXgxNgÍúÌÛðßÌ_¶É¨¯éñíÉdvÈTOÅ éªA
2000NÌP. CousotÌ_¶uÛðßF»ÌB¬ÆW]vÅÍAÌæ¤È®ÆµÄ\»³êéæ¤É
ÈÁ½i·Èí¿A»±ÅÍReLXgâReLXgxNgÆ¢¤¾tÍàÍâ\ÉoÈÈÁ½jG
uÛðßÌߪÀÛÉgpµÄLøÅ éÆ¢¤±Æð¼´Iɦ·½ßÉAÀS«ÌðÍ(safty analysis)ðl¦éBi^CG[ª¶ÝµÈ¢Æ¢¤æ¤ÈjÀS«Æ¢¤«¿ÍA½©«¢±ÆÍN«È¢AܽÍvOÌÀsÍSÈóÔÌÜÜÅ éAÆ¢¤±ÆðKè·éB±ÌTOÍȺÅྷéæ¤ÉÛÌ¡(composition)Éæè讻ūéBÅÌÛÍA±Ìg[XÉÁÄ»êéóÔÌWÉæég[XÌÛÅ éF¿S(Ð)={Ðk F k¸[0, |Ð|]}
g[XÌWXÌßÍAWXÌÈÆàêÂÌg[Xð\·óÔÌWÅ éF
@@@@@@@@@@@¿S(X)=¾Ð¸X¿S(Ð)
¿S(X)ªsÏ(invariant)Å éÆÍAvOðÀsµÄúóÔ©çBÂ\ÈSÄÌóÔª»Ì«¿ð½³È¯êÎÈçȢƢ¤±ÆðÓ¡·éB
@óÔsÍAvOCÌvO|Cgl (¸C)ÆA®l(x1, ... ,xn)¸ZðæévOCÌÏX1, ... ,Xnix1¸X1, ... , xn¸Xn)ðwè·é§äóÔ©ç\¬³êÄ¢éÆ·éBåÇIÈsÏ®
¿S(X)ÍA»Ì|CgÅevO|CgÆÏÌÂ\ÈlÌgÌWðÖWïéAÇIÈsÏ®ÌxNgɯ^(isomorphic)Å éF
@@@@@@@@@@@@¿l(Y)=®l¸C{(x1, ... ,xn)F(l, (x1, ... ,xn))¸Y}@EEEEi®Pj
±Ìæ¤Ég[XÌvOWÌvZÍn³®óÔZnÌ_ÌWÉæèß³êéBv
±Ìè`ðCousotÌú_¶ÅÌuóÔvÌè`ÆÎä·éÆA
óÔStateÍ<Arc, Env>ÌgÅ èAvOÀsÌ évO|CgÅÌvOÌóÔð¦·iStates = Arcs~EnvjB¨}QDPPQÆB
@@@
@@@@@@@@@@@@}QDPP@óÔÌà¾
@@i®PjÍãLÌáÌêAC={r0, r1, r2, r3, r4, r5, r6"A®lx¸Env=ZAYÍóÔÌWÅ èA
@@@@¿l(Y)=®l¸C{(x1, ... ,xn)F(l, (x1, ... ,xn))¸Y}=®l¸C{ x¸ZF(l, x)¸Y}
@@@@@¨±Ì®ÌÓ¡ðCousotÌú_¶Ì¾tÅ\»·éÆA
@@@@@@{ x¸ZF(l, x)¸Y}@Ì@vO|CglÅÌReLXgCḻÆB
@@@@evO|Cgl¸CÉReLXgðÖW³¹éxNgªReLXgxNgÈÌÅA
@@@@@@®l¸C{ x¸ZF(l, x)¸Y}@Ì@vOCÌReLXgxNg̱ÆB
@@@±Ìæ¤Éú_¶ÌTvvOÌg[XÍ1³®óÔZÌ_ÌWÉæèß
@@@³êéB
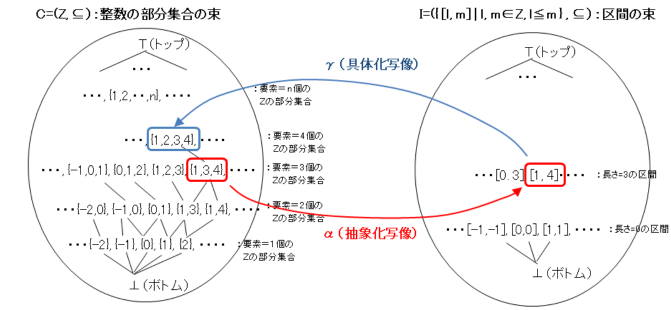
QDQ@vOÌÛðß@@@@@@@@@@@@@@@@@@@@@@
@QDPßÅÍAvOÌÏÌæélÉ ÚµÄAReLXgÆReLXgxNgÆ¢¤QÂÌTOð±üµAReLXgxNgÌs®_ðßé±Æðc_µ½B±±ÅÍA±êçÌTOð³ÉÛðßðtH[}Éè`·éBܽAæèP»³ê½¢EÅReLXgxNgÌs®_ðßé½ßÉA¯¶vOPÉηé¡ÌÛðßÔÌKAÚ±ªoê·éBi±ÌßÍCousotú_¶ÌTß`WßÉYj
QDQDP@ReLXgÆReLXgxNgÉÖW·éÚ
@QDPß©çAReLXgÆReLXgxNgÌ¢EðÁ¥t¯éÚð®·éÆAºLÌæ¤ÉÈèAeڪεĢéG
@ReLXgÉÖW·éÚÍA
@EContexts
@iEa¾j@@@@@iFQDPßÅÍA¾Í¾`Ìè`̽ßÉgpµ½j
@iE¼ºj@@iFQDPßÅÍAºÍº`Ìè`̽ßÉgpµ½j
@EÅå³=Envi«j
@EŬ³=ÓióWj
@EÌReLXgðßén-contextÖ
AReLXgxNgÉÖW·éÚÍA
@EContext vectors
@Ea¾`
@E¼º`
@EÅå³= T`(CÓÌr¸ArcsÉεÄAT`(r)=Env )
@EŬ³=Û`iCÓÌr¸ArcsÉεÄAÛ`(r)=Ój
@EÌReLXgxNgðßéF-contÖ
»±ÅAQDQßÅÍAãLÌÚð³ÉêÊ»µÄAÛðßÌ`®è`ðs¤B
AµAÛðßÌ`®è`ÌOÉA»ÌõƵÄQDQDQż©(semilattice)Ìè`ðq×éB
QDQDQ@¼©(semilattice)
@è`F@Lª¼©Å éÆÍACÓÌx, y, z¸LÉεĺLð½·Zª
@è`³ê½ãL=(L,j̱ÆÅ éG
@@@@(i)@xx=x
@@@@(ii)@xy=yx
@@@@(iii)@x(yz)=(xy)z
@±ÌÆ«AºLÌ説§·éG
@èF@¼©Lɨ¢ÄAx yðxy=yÉæèè`·éÆA(L,
yðxy=yÉæèè`·éÆA(L, )ÍCÓÌvfÌg
)ÍCÓÌvfÌg
@ªãÀð¼WÉÈéijB
@ؾF@ܸA ª¼Å é±Æð¦·G
ª¼Å é±Æð¦·G
@@@@(i) xx=xÍè`æèx xðÓ¡µÄ¢éB
xðÓ¡µÄ¢éB
@@@@(ii) x y©Ây
y©Ây xÈçÎAxy=y©Âyx=xµ½ªÁÄAx= yx= xy=yÆÈèAx=y
xÈçÎAxy=y©Âyx=xµ½ªÁÄAx= yx= xy=yÆÈèAx=y
@@@@(iii) x y©Ây
y©Ây zÈçÎAxz= x(yz)= (xy)z=yz=z@]ÁÄAx
zÈçÎAxz= x(yz)= (xy)z=yz=z@]ÁÄAx z
z
@@@@ÉAx(xy)=(xx)y=xyÈÌÅAx xy
xy
@@@@¯lÉAy(xy)=y(yx)= (yy)x= yx= xyÈÌÅAy xy
xy
@@@@µ½ªÁÄAxyÍ{x, y}ÌãEÅ éB
@@@@¡Ax z, y
z, y zÆ·éÆA(xy)z=x(yz)=yz=zÈÌÅA(xy)
zÆ·éÆA(xy)z=x(yz)=yz=zÈÌÅA(xy) z
z
@@@@µ½ªÁÄAxyÍ{x, y}ÌãÀÅ éB
@@@ij¯lɵÄAy xðxy=xÉæèè`·éÆA(L,
xðxy=xÉæèè`·éÆA(L, )ÍCÓÌvfÌgªºÀðÂ
)ÍCÓÌvfÌgªºÀðÂ
@@@@@@¼WÉÈé
ÈãÌõð³ÉÌQDQDRÅÛðßÌ`®è`ð^¦éB
QDQDR@ÛðßÌ`®è`
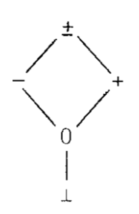
@QDQDPß©çAReLXgÌ¢EðKè·éÚðg(tuple)Ì`®Å\·ÆA
@@@@@@@Contexts,i¾j,iºj,Env,Ó, n-context
ÆÈéB±êͼºÉÖµ®õ©ÆÈÁÄ¢éiÅå³ÍEnv,Ŭ³ÍÓjB
@vOPÌÛðßÌ`®è`ÍA±êðêÊ»µ½àÌÅ éG
è`F@vOPÌÛðßÌ`®è`ÆÍAºLÌg̱ÆÅ éG
@@@@@@@@@I=A-Cont,, , T,Û, Int
, T,Û, Int
@@±±ÅA
@@EA-ContFvOPÌÛReLXgijÌWB
@@@@@@ijvOÌReLXgÍvOÌSÄÌÂ\È«ÌWÅ éªA
@@@@@@@ÛReLXgÍReLXg»ÌàÌÅà梵A±êðP»µ½àÌÅàæ¢B
@@@@@@@á¦ÎA évO|CgÅϪ{0, 1, 2, 3, 4, 5}Ìlðæè¾éêA
@@@@@@@±êðP»µÄ¼[Ì[0, 5]ðl¦éÈÇB@
@@EÆ FÍ@(i) xx=xA(ii) xy=yxA(iii)x(yz)=(xy)zð½·ZB
FÍ@(i) xx=xA(ii) xy=yxA(iii)x(yz)=(xy)zð½·ZB
@@@@@@@@ Íx
Íx yÌxy=yÉæèè`³ê½¼Å èAA-Cont,
yÌxy=yÉæèè`³ê½¼Å èAA-Cont,
@@@@@@@@Í®õ|¼©Å éB
@@@@@@@@¨A-ContÌÅå³ÍTBܽAA-ContÍŬ³ÛðÂàÌÆ·éB
@@ETFA-contÌgbvAÛFA-ContÌ{g
@@EIntFvOoÌÊ(arc) rÆÛReLXgxNgA-Cont`ijðüÍƵAvOP
@@@ÌÛReLXgðÔ·ÖB
@@@ijÛReLXgxNgÍAeÊrÉηéÛReLXgð¬ªÆ·éxNgÅA
@@@@@@@@A-Cont`ir)=Int(r,A-Cont`)
@@ܽAQDQDPß©çAReLXgxNgÌ¢EðKè·éÚðg(tuple)Ì`®Å\·ÆA
@@@@@@@Context vectors,¾`,º`,T`,Û`, F-cont
ÆÈéBQDPßiUjÅÌc_©ç±ÌgÍ®õ©ÉÈéB
vOPÌÛðßÌ`®è`ÅÍA±ÌReLXgxNgÌ¢EàÌæ¤Éè`·éB
è`@vOPÌÛðßÌ`®è`IÉηéÛReLXgxNgÌ`®è`ÆÍA
EÌg̱ÆÅ éF@< A-Cont`,`, `, T`,Û`, Int`>
`, T`,Û`, Int`>
QDPßiVjÅÌc_©ç±ÌgÍ®õ©ÉÈéB
@ÛðßÌ`®è`ÌÚÆQDPßÌáÆÌÎðZßéÆAÌæ¤ÉÈéBÛðßÌ`®è`
ÌeÚÌïÌIC[WƵĻÌÎÖWðªÉüêĨÆæ¢B
@ReLXgÉÖW·éÚÍA
@ÛðßÌ`®è`@@@@@@@@@@@@@@QDPßÌá
@@EÛReLXgA-Cont@@@@@@@@@@@@@Ì@@EContexts
@@EZ@@@@@@@@@@@@@@@@@@@@@@@@@@@@@Ì@@@iEa¾j@
@@E¼![]() @@@@@@@@@@@@@@@@@@@@@@@@@Ì@@iE¼ºj
@@@@@@@@@@@@@@@@@@@@@@@@@Ì@@iE¼ºj
@@EÅå³T@@@@@@@@@@@@@@@@@@@@@@@Ì@@EÅå³=Envi«j
@@EŬ³Û@@@@@@@@@@@@@@@@@@@@@@Ì@@EŬ³=ÓióWj
@@EÌÛReLXgðßéIntÖ@@Ì@@EÌReLXgðßén-contextÖ
AReLXgxNgÉÖW·éÚÍA
@ÛðßÌ`®è`@@@@@@@@@@@@@@QDPßÌá
@@EÛReLXgxNgA-Cont`@@@@Ì@EContext vectors
@@EZ`@@@@@@@@@@@@@@@@@@@ Ì@Ea¾`
@@E¼![]() `@@@@@@@@@@@@@@@@@Ì@E¼º`
`@@@@@@@@@@@@@@@@@Ì@E¼º`
@@EÅå³= T`@@@@@@@@@@@@@@@@@Ì@EÅå³= T`(CÓÌr¸ArcsÉεAT`(r)=Env )
@@EŬ³=Û`@@@@@@@@@@@@@@@@@Ì@EŬ³=Û`iCÓÌr¸ArcsÉεAÛ`(r)=Ój
@@EÌÛReLXgxNgð@@@@@Ì@EÌReLXgxNgðßéF-contÖ
@@@ßéInt`Ö@@@
QDQDS@ÛðßÌêÑ«
@êÊÉAvOÌÛðßÍPÂÆÍÀçÈ¢iÛReLXgÌ^¦ûÉæéjBµ½ªÁÄA
@@@EæèvOÉߢÛðßibj¨±êðuhïÌhðßvÆྤB
@@@EæèP»³ê½Ûðßi`j¨±êðuhÛhðßvÆྤB
ðìèAbÆ`ɩ̼ÖWðÛ¶·éæ¤ÈKØÈÊð\¬·é±ÆªÅ«êÎAP»³ê½AÅâèðð¯ÎÇ¢±Æª¦³êéBQÂÌÛðßɱÌæ¤ÈÎÖWª é±ÆðuÛðßÌêÑ«(Consistent Abstraction Interpretations)vÆ¢¤B
uKAÚ±vͱÌÎÖWƵÄoê·éi}QDPQQÆjB
@@@@@@@
@@@@@@@@@}QDPQ@¡ÌÛðß
@ãḺÆðµ§Éè`·éÆÌæ¤ÉÈéB
è`iÛðßÌêÑ«jF@@¡AvOÌQÂÌÛðߪ Á½ÆµA
@@êûÍAvOÌhÛhðßI|=< A-Cont|,|, |, T|,Û|, Int|>A
|, T|,Û|, Int|>A
@@¼ûÍhïÌhðßI = < C-Cont,, ,±,Û, Int>Å éÆ·éB
,±,Û, Int>Å éÆ·éB
@@±êÉηéReLXgxNgÌ©ÍAºLÅ éG
@@@@@I|ÉηéàÌF@< (A-Cont|)`, (|)`, ( |)`, (T|)`, (Û|)`, (Int|)`>
|)`, (T|)`, (Û|)`, (Int|)`>
@@@@@IÉηéàÌF@< C-Cont`,`, `, T`,Û`, Int`>
`, T`,Û`, Int`>
@@±ÌÆ«AhÛhðßI|=< A-Cont|,|, |, T|,Û|, Int|>ªA
|, T|,Û|, Int|>ªA
@@hïÌhðßI = < C-Cont,, ,±,Û, Int>ÆêÑ«ª éÆ¢¤±ÆÍA
,±,Û, Int>ÆêÑ«ª éÆ¢¤±ÆÍA
@@I|©ç¶¶éReLXgxNgCv|ªAæèÚ×ÈðßI©ç¶¶éReLXg
@@xNgCv̳µ¢ßÉÈÁÄ¢éê̱Æð¾¤B
@±±ÅA³µ¢ßÆÍAºLÌ(1),(2)ª¬§·é±ÆÅ éG
(1)ReLXgÌ¢EÅAC-ContÆA-Cont|ÔÉKA}üÌÎÖWª¶Ý·éG
@·Èí¿AÊ¿FC-Cont¨A-Cont|,ÁFA-Cont|¨C-ContÉεAºLª¬§·éG
@@@@@@¿AÁÍP²ÖÅ éB@@@@@@@@@@@@@@@@EEEE(G1)
@@@@@ACÓÌx¸C-ContÉεÄAx![]() Ái¿ixjj@EEEE(G2)
Ái¿ixjj@EEEE(G2)
@@@@@BCÓÌx|¸A-Cont|ÉεÄAx|=¿iÁix|jjEEEE(G3)
(2)ReLXgxNgÌ¢EÅAC-Cont`Æ(A-Cont|)`ÔÉKAÚ±ÌÖWª¶Ý·éG
@·Èí¿AïÌReLXgxNgÆÛReLXgxNgÔÌÎi¿`FÛ»jÆtÌÎ
@iÁ`FïÌ»jźLð½·Ê¿`,Á`ª¶Ý·é±ÆÅ éB
@@@@@@@@@@@@@@{Cv `Á`(Cv|)}©Â{¿`(Cv)
`Á`(Cv|)}©Â{¿`(Cv) `Cv|)}EEEE(G4)@ij
`Cv|)}EEEE(G4)@ij
@ãLÌè`Åoê·éÚð}¦·éÆA}QDPRÌæ¤ÉÈéB
@@@@@
@@@@@@@@@@@@@@}QDPR@ÛðßÌêÑ«ÌÖW}
ijð(G4)ÍCÓÌrÉεĬ§·éåÇIȼ辪AÀÛÉͱêÌãíèÉvOÌ
@@ïÌÆÛðßÉ¢ÄÌȺÌÇI¼èªgp³êéF
@@@{CÓÌ(r, x|)¸Arc~(A-Cont|)`ÉεAInt(r,Á`(x|)) Á(Int|(r, x|))
Á(Int|(r, x|))
@@@©Â
@@@ {CÓÌ(r, x)¸Arc~C-Cont`ÉεA¿(Int(r, x)) |Int|(r,¿`(x))@@EEEE(G5)
|Int|(r,¿`(x))@@EEEE(G5)
@@¨(G5)ÍAÛReLXgðßéÖInt|ªS(Sound)Å é±Æð¦µÄ¢éB
@@@@·Èí¿AhïÌhðßÌ¢EÅß½ReLXgInt(r, x)ðۻʿÅÚµ½
@@@¿(Int(r, x))ÍAhÛhðßÌ¢EÅß½ÛReLXgInt|(r,¿`(x))ÉÜÜêéB
¡ÛðßÌêÑ«ÌáPFæÔÌ©
@@PðPêÌ®ÏxÌvOÆ·éB
±ÌÆ«A«EnvÍ®SÌZiÏÌljÅ éBµ½ªÁÄAvOPÌPÂÌÛðßƵÄ
@@@@@@@@I=ZÌxLW,i¾j,iºj, T=Z¾{|,+},Û=Ó, n-context
ªl¦çêéB
@±±ÅAReLXgCÍ®Ì éWÅ éªA±êÍÂæÔ¿(C)=[min(C), max(C)]ÉæèÛ»³êéBCªLÀÅȢƫ«EÍ|ܽÍ+ÉÈéBܽAtÌÎÁ([a, b])={x| a x b}@Æ·éB±ÌÆ«AæèÛIÈÛðßIIiTtBbNXÍIntervalÌÓ¡j
@@@@@@@@II=æÔÌxLW,i¾j,iºj,T=[|,+],Û=Ó, n-context
ª\¬Å«A¿(C)=[min(C), max(C)],Á([a, b])={x| a x b}ÍKA}üÉÈÁÄ¢éB
i±êÌn-contextÉ¢ÄÍÅÅྷéj@±êð}¦·éÆ}QDPSÌæ¤ÉÈéB
@@
@@@@@@@@@@@@@@@@@}QDPS@®ÆæÔÌKAÚ±
@ãLÅÍAÎÛÌvOPðuPêÌ®ÏxÌvOÆ·éBvÆêÊIÉq×½ªA
ïÌIȺLÌvOÉεÄReLXgxNgÌŬs®_ðßéB
@@@@@@@@@@@@@@@@@@@
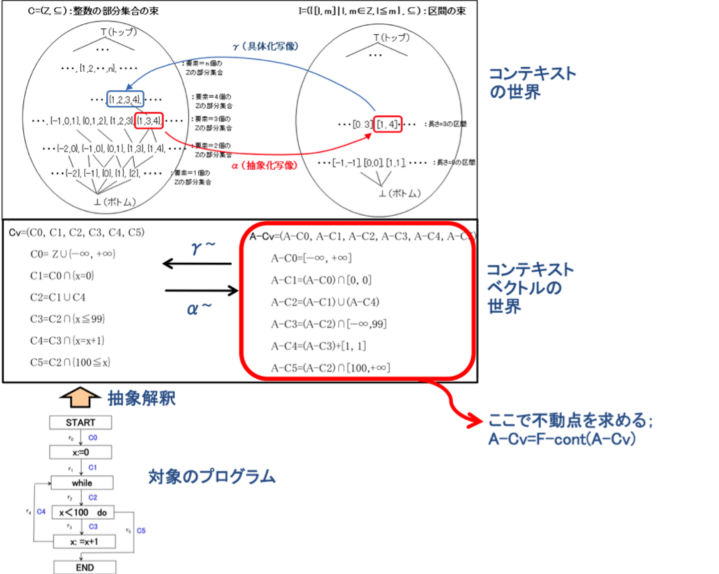
@@@@@@@@@@@@@@@@@@@}QDPT@ÎÛvO
@}QDPTÌC0, C1,EEE, C5ÍReLXgxNgÌeÊÉη鬪ƷéBµ½ªÁÄAReLXgxNgCvÍACv=(C0, C1, C2, C3, C4, C5)Æ\³êéBvOÌÏxÍ®ZÅ éBÊr0ÌReLXgiÊr0ÅÌÏxÌæélÌWjÍsèÈÌÅC0=Z¾{|, +}
n-contextÖÍCv(r)=n-context(r,Cv)ÈÌÅA
C1=Cv(r1)=n-context(r1,Cv)=C0¿{x=0}@©n-contextÖÌè`©çAr1ÅÌReLXgÍr0ÅÌ
@@@@@@@@@@@@@@@@@@@@@@@@@@@ReLXgÆr1̼OÌ®ÌlÌWÆÌÏW
@@@@@@@@@@@@@@@@@@@@@@@@@@@ir0Ær1ͼñ̽ßÏWÆÈéj
C2=Cv(r2) =n-context(r2,Cv)=C1¾C4@@©n-contextÖÌè`©çAr2ÅÌReLXgÍr1ÅÌ
@@@@@@@@@@@@@@@@@@@@@@@@@@@@ReLXgC1Ær4ÅÌReLXgC2ÆÌaWB
@@@@@@@@@@@@@@@@@@@@@@@@@@@ir2Ír1Ær4̬̽ßaWÆÈéj
¯lɵÄA
C3= Cv(r3) =n-context(r3,Cv)=C2¿{x 99}
C4= Cv(r4) =n-context(r4,Cv)=C3¿{x=x+1}
C5= Cv(r4) =n-context(r4,Cv)=C2¿{100 x}
µ½ªÁÄA}QDPQÌvOÉηéReLXgxNgCvª®ÌWƵÄÜÁ½G
Cv=(C0, C1, C2, C3, C4, C5)
@@@C0= Z¾{|, +}
@@@C1=C0¿{x=0}
@@@C2=C1¾C4
@@@C3=C2¿{x 99}
@@@C4=C3¿{x=x+1}
@@@C5=C2¿{100 x}
±±ÅAKA}üÉæéReLXgÌÛ»¿(C)=[min(C), max(C)],Á([a, b])={x| a x b}ðReLXgxNgÉKp·éÆAÛReLXgxNgA-CvÍÌæ¤ÉÈéG
A-Cv=(A-C0, A-C1, A-C2, A-C3, A-C4, A-C5)
@@@A-C0=[|, +]
@@@A-C1=(A-C0)¿[0, 0]
@@@A-C2=(A-C1)¾(A-C4)
@@@A-C3=(A-C2)¿[|,99]
@@@A-C4=(A-C3)+[1, 1]
@@@A-C5=(A-C2)¿[100,+]
ãLÍæÔÉÖ·éZ̮ŠéB±±ÅAæÔÌZͺLÉæèè`³êéàÌÆ·éG
@@E [a, b]¾[c, d]=[min(a, c), max(b, d)]
@@E [a, b]¿[c, d]=[max(a, c), min(b, d)]
@@E [a, b]+[c, d]=[a+c, b+d]
@ReLXgxNgÔÌKAÚ±i¿`,Á`jͺLÆÈéG
@¿`(Cv)=(¿(C0),¿(C1),...,¿(C5))=([min(C0), max(C0)], [min(C1), max(C1)],...,[min(C5), max(C5)])
@Á`([a0, b0],[a1, b1],...,[a5, b5])=({x| a0 x b0 },{x| a1 x b1",...,{x| a5 x b5 })
ÈãÌSÌð}¦·éÆA}QDPUÌæ¤ÉÈéB
@@@
@@@@@@@}QDPU@vOÌÛðßSÌÌá
@}QDPUð©éÆAvOÌQÂÌÛðߪsíêÄ¢éBPÂÍÏÌWð®Ì©Æµ½hïÌhðßÅ èAà¤êÂÍÏÌWðæÔ̩Ƶ½hÛhðßÅ éB±êÍKA}ü(¿AÁjÉæèÎt¯çêÄ¢éBܽA±êçÌReLXgÉεÄReLXgxNgª®ÌWƵÄeX\»³êÄ¢ÄA»êçÉÍKAÚ±i¿`,Á`jªÎµÄ¢éB
@ÅIIÉs¢½¢±ÆÍAhÛhðßÌ¢EÅReLXgxNgÌŬs®_ðßé±ÆA·Èí¿AReLXgxNgÌ®ÌVXeA-Cv=(A-C0, A-C1, A-C2, A-C3, A-C4, A-C5)
@@@@@@A-C0=[|, +]
@@@@@@A-C1=(A-C0)¿[0, 0]
@@@@@@A-C2=(A-C1)¾(A-C4)
@@@@@@A-C3=(A-C2)¿[|,99]
@@@@@@A-C4=(A-C3)+[1, 1]
@@@@@@A-C5=(A-C2)¿{100 x}
ɨ¢ÄA»Ìs®_A-Cv=F-Cont(A-Cv)ðßé±ÆÅ éB
@®ÌVXeÌs®_ðßéû@ÉÍAN[lÌV[PXijðvZ·éh½hASYª éF·Èí¿AÛ`©çoµÄAInt`(Û`) Int`(Int`(Û`))
Int`(Int`(Û`)) ...ðJèÔµA±êÌŬs®_¾{Int`n(Û`) | n¸N}ðCvÆ·éB
...ðJèÔµA±êÌŬs®_¾{Int`n(Û`) | n¸N}ðCvÆ·éB
ijN[l`FC(Kleene chain)ÆྤBLð®õ¼WƵAf:L¨LðScottA±ÖÆ·éB±ÌÆ«ALÌŬ³Û©çfð½·é±ÆÉæè¾çêéºLÌ`FCðã¸N[l`FC(ascending Kleene chain)Æ¢¤F
@@Û f(Û)
f(Û)  f(f(Û))...
f(f(Û))...  fn(Û)
fn(Û)  ...@
...@
@ÌQDQDTßÅÍAReLXgxNgÌ®ÌVXeA-Cv=(A-C0, A-C1, A-C2, A-C3, A-C4, A-C5)Ìs®_A-Cv=F-Cont(A-Cv)ð½ASYÅÀÛÉð¢ÄÝéB
[ÅßÌ_¶©çÌß]
2000NÌP. CousotÌ_¶uÛðßF»ÌB¬ÆW]vÅÍAvO̧äÌ|CgÉt¯çê½®ÏÌlÌæÔÉæèAg[XÌWðÛ»·é±ÆÍÛ̬
@@@@@@@@@@@@@@@¿(T)=¿i(¿r(¿l(¿S(T))))
Éæè^¦çêéB
±±ÅA¿SÍg[XÉÁÄ»êéóÔÌWÉæég[XÌÛÅ éG
@@@@@@@@@@@@@@¿S(Ð)={ÐkF k¸[0, |Ð|]}
¿lÍóÔÌWYÉReLXgxNgðγ¹éG
@@@@@@@@@@@@@@¿l(Y)=®l¸C{(x1, ... ,xn)F(l, (x1, ... ,xn))¸Y}
¿rÍvOÏÌÔÌÖWð³µ½ÏÌæÌßÅ éF
@@@@@@@@@@¿r(X)= ®i=1,..,n{xiFÎx1, ... ,xi-1, xi+1, ... ,xnF(x1, .,xi ,.. ,xn)¸X}
±êÍeÏÌÖWð³µ½¼ÏÌæð¦µÄ¢éBCousotÌú_¶ÌTvvOÍA
P³ÌReLXgÌ¢EÈÌÅ¿r(X)ÍPÊÆÈéBܽACousotÌú_¶ÌTvvOÅÍA±Ìªi¿i(Z)=[min Z, max Z]jªKAڱƵÄླêÄ¢½B
µ½ªÁÄA¿(T)=¿i(¿r(¿l(¿S(T))))ðCousotÌú_¶ÌTvvOÅÎä·éÆA
}QDPUɨ¢ÄA
@@TÌ ÎÛÌvOÌg[XÌW¨±Ìg[XÉÁÄ»êéóÔÌWÐðl¦éB
@ ¿S(T)Ì¿S(Ð) = {Ðk F k¸[0, |Ð|]}={ÐkFk¸[0, 303]}={Ð0,Ð1,Ð2,EEE,Ð302,Ð303 } (=¿S(X) )=Y
@¿l(¿S(T))Ì¿l(¿S(Ð))=¿l(Y)=®l¸C{(x1, ... ,xn)F(l, (x1, ... ,xn))¸Y}=®l¸C{ x¸ZF(l, x)¸Y}
@@@@@@@@@@@@@@@@@=vOCÌReLXgxNgi¨ºÌ}ÌCvð\¬·éÜÅj
@¿r(¿l(¿S(T))Ì¿r(¿l(¿S(T))=¿l(¿S(Ð))©P³Ì¢EÅl¦Ä¢éÌÅ¿rÍPÊB
@@¿i(¿r(¿l(¿S(T))))Ì¿i(Z)=[min Z, max Z]@i}QDPUÌۻʿÉYj
iâ«à¾Fg[XZ}eBNXðæÔÅÛ»·é±Æð}¦·éÆA
@@@@@@@
@@@@@@}QDPV@g[XZ}eBNXÌæÔÉæéÛ
¡ÛðßÌêÑ«ÌáQFÌK¥@i±ÌªÍA¶£ÌTæèj
@ÛðßÌÅ༴IÈáÍÌK¥Å éBÌK¥ÆÍAXðÆ·éÆ«
@@@@@@EXªÌÈçÎ-1
@@@@@@EXª0ÈçÎ0
@@@@@@EXª³ÈçÎ+1
ðγ¹éK¥Å éB
á¦Î-1515*17ÍAZpZÌÓ¡_ªÌ[Åè`³ê½Û¢E{(+), (-), (})}ÅÌvZð¦·àÌƵÄð³êéB-1515*17ÌÛ¢EÅÌÀsÍ-(+)*(+)¨ (-)*(+)¨(-)ÆÈèA-1515*17ÍÌÆÈéBÛðßÍÊíÌvZ¢EÌÁÊÈ\¢i±ÌáÅÍjÉÖW·éB»êÍÀÛÌÀsÌ é¤ÊÌvñð^¦Ä¢éB
@¡AZð®ÌWƵA{-1, 0, 1}ðÌWÆ·éB
ZÌxLW2ZÆ{-1, 0, 1}ÌxLW2{-1, 0, 1}ÆÌÔÌÎ
@@@@¿F2Z@¨@2{-1, 0, 1}"ÁF2{-1, 0, 1}¨@2Z@
ðAÌæ¤Éè`·éG
@@@@¿({z1,z2,...,zn})={z1Ì, z2Ì,...,znÌ}
@@@@Á({-1})=Ì®SÌ,Á({0})={0},Á({-1,0})={0}¾Ì®SÌ
@@@@Á({1})=³Ì®SÌ,Á({0,1})={0}¾³Ì®SÌ,Á({-1,1})=0ð®SÌ,
@@@@Á({-1,0,1})=Z
@@@@@iáj¿({-1,-2,-7})={-1},¿({0,-2,-5})={-1,0},¿({0,2,4,14,5,10,35})={0,1}
@@±ÌÆ«i¿AÁjÍKA}üÆÈéB
@@@¾ç©ÉÁ(¿({z1,z2,...,zn}))=Á({z1Ì, z2Ì,...,znÌ})»{z1,z2,...,zn}
@@@@ÈÌÅAX¸2Z@Æ·éÆ«AXºÁ(¿(X))ÆÈéBEEE@
@@@@ܽA¿(Á({-1}))=¿(Ì®SÌ)=-1,¿(Á({0}))={0},
@@@@@¿(Á({-1,0}))=¿({0}¾Ì®SÌ)={-1,0}
@@@@@¿(Á({1}))=¿(³Ì®SÌ)={1},¿(Á({0,1}))=¿({0}¾³Ì®SÌ)={0,1},
@@@@@¿(Á({-1,1}))=¿(0ð®SÌ)={-1,1},¿(Á({-1,0,1}))=¿(Z)= {-1,0,1}
@@@@ÈÌÅAY¸2{-1, 0, 1}Æ·éÆ«AY=¿(Á(Y))ÆÈéBEEEA
@@@@@AAæèi¿AÁjÍKA}üÅ éB
@@@@ÌK¥ÉæéÛðß̩ͺLÌæ¤ÉÈéB
@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@}QDPW@@ÌK¥Ì©
@@@ÉA®ÌWÔÌaâÏÍۻʿÅǤÈé©ðl¦ÄÝéB
á¦ÎA®ÌWÔÌÏ
@@@@@@@@@{-1,-2,-7}*{0,-2,-5}={0,2,4,14,5,10,35}@EEEB
ðl¦éBB̶ÓÌeXð¿ÅÚ·ÆA¿({-1,-2,-7})*|¿({0,-2,-5})={-1}*|{-1,0}={1,0}
êûABÌEÓð¿ÅÚ·ÆA¿({0,2,4,14,,5,10,35})={1,0}@]ÁÄAºLª¬§G
@@@@@@@¿({-1,-2,-7}*{0,-2,-5})=¿({-1,-2,-7}) *|¿({0,-2,-5})
·Èí¿AÛ¢EÅÌÏ·iÏjÍïÌ¢EÅÌÏ·iÏjð¿ÅÚµ½àÌɵÈéB
®ÌWÔÌÏÅͱꪬ§·éªA±êðAÛÏ·Ì®S«(completeness)Æ¢¤B
@@@
@@@@@@}QDPX@®ÌWÔÌÏÌÛ»
Éá¦ÎA®ÌWÔÌa
@@@@{-3,-4,-7}+{1,2,3}={-2,-3,-6,-1,-2,-5,0,-1,-4}EEEC
ðl¦éBC̶ÓÌeXð¿ÅÚ·ÆA¿({-3,-4,-7})+|¿({1,2,3})={-1}+|{1}={-1,0,1}
êûACÌEÓð¿ÅÚ·ÆA¿({-2,-3,-6,-1,-2,-5,0,-1,-4})={-1,0}@]ÁÄAºLª¬§G
@@@@@¿({-3,-4,-7}+{1,2,3})º¿({-3,-4,-7}) +|¿({1,2,3})
·Èí¿AÛ¢EÅÌÏ·iajÍïÌ¢EÅÌÏ·iajð¿ÅÚµ½àÌðÜÞB
®ÌWÔÌaÅͱꪬ§·éªA±êðAÛÏ·ÌS«(soundness)Æ¢¤B
@@@@
@@@@@@@@@}QDQO@®ÌWÔÌaÌÛ»
@êÊÉAP, AFW@P=2P,A=2AƵA
@@@@¿:P¨AðÛ»ÊiãÌáÅÍÌK¥Éγ¹é¿j
@@@@FFP¨PðPãÌÏ·Æ·éiãÌáÅÍa(+)âÏ(*)j
@@@@F~ð¿(P)=AãÌÛÏ·Æ·éBF~FA¨AiãÌáÅÍÛ»ÅÌa(+|)âÏ(*|)j
@±ÌÆ«AÛÏ·F`ªSÅ éÆÍACÓÌp¸PÉεÄA¿(F(p))ºF`(¿(p))
@ܽAÛÏ·F`ª®SÅ éÆÍACÓÌp¸PÉεÄA¿(F(p)) = F`(¿(p))
@@@@@
@@@@@
@@@@@@@@@@@@}QDQP@ÛÏ·
QDQDT@Ûðßžçê½®QÌð@i½ASYj
@Ûðßžç꽺LÌ®Qðð±Æðl¦éBi±±ÅÍAReLXgÌϼð
@A-C0¨X0, A-C1¨X1, A-C2¨X2, A-C3¨X3, A-C4¨X4, A-C5¨X5Æu·¦Äl¦éj
@@@@@@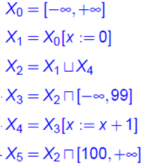
@±êÍX2ªÜêÎX3È~Í·®Éª©éÌÅAÌâèƵÄÝèÅ«éG
yâèzºLÌvOðÀsµ½Æ«ÌAvOÌX2ÅÌÏxÌæè¾élÌÍÍðvOðÍÅßæB
@@@@@@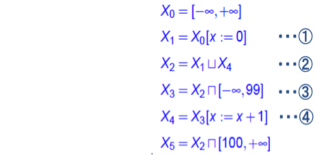
@AA©çX2ÌlðÏxÅ\·ÆAiÈ~ @
@ @ð¾A¿Å\·j
@ð¾A¿Å\·j
@X2=X1¾X4=X1¾(X3[x:=x+1])=X1¾((X2¿[-, 99])[x:=x+1])=[0, 0]¾((X2¿[-, 99])[x:=x+1])
]ÁÄA@X2=[0, 0]¾((X2¿[-, 99])[x:=x+1])
±êÍX2ÉÖ·éÄA®Å éB
ãÅß½ºLÌ®©çX2ðßéÉÍH
@@@@@@@@X2=[0, 0]¾((X2¿[-, 99])[x:=x+1])@ EEED
y]Ìf[^t[ðÍÌû@z
@EÌlðŬ³©çnßÄA®DðiËi+1ÌP²å·éQ»®EÉæèA±êÈãxÌæè¾é
@ Íͪ¦È¢is®_jÉB·éÜÅJèÔµvZ·éG
@@@@X2(i+1)=[0, 0]¾((X2(i)¿[-, 99])[x:=x+1])@EEEE
@@±Ì®ð¼ÌŬ³Ûi±±ÅÍóWÓÆl¦ÄÇ¢j©çoµÄßÄ¢ÆA
@@@@@@@@@@@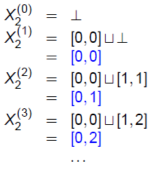
@@ãLª¬§·é±ÆÍE®©ç·®Éª©éG
@@@X2(1)=[0, 0]¾((X2(0)¿[-, 99])[x:=x+1]) = [0, 0]¾(Û¿[-, 99])[x:=x+1])
@@@@@=[0, 0]¾(Û)[x:=x+1])=[0, 0]¾(Û)=[0, 0]
@@ X2(2)=[0, 0]¾((X2(1)¿[-, 99])[x:=x+1]) = [0, 0]¾([0, 0]¿[-, 99])[x:=x+1])
@@@@@@=[0, 0]¾([0, 0])[x:=x+1])=[0, 0]¾([1, 1])=[0, 1]
±êðJÔ·Æi100ñÊjA
@@@@@@@@@EEEE
@@@X2(99)=[0, 98]
@@@X2(100)=[0, 0]¾((X2(99)¿[-, 99])[x:=x+1])=[0, 0]¾(([0, 98]¿[-, 99])[x:=x+1])
@@@@@@@@=[0, 0]¾(([0, 98])[x:=x+1])=[0, 0]¾(([1, 99])=[0, 99]
@@@X2(101)=[0, 0]¾((X2(100)¿[-, 99])[x:=x+1])=[0, 0]¾(([0, 99]¿[-, 99])[x:=x+1])
@@@@@@@@=[0, 0]¾(([0, 99])[x:=x+1])=[0, 0]¾(([1, 100])=[0, 100]
@@@X2(102)=[0, 0]¾((X2(101)¿[-, 100])[x:=x+1])=[0,0]¾(([0,100]¿[-,99])[x:=x+1])
@@@@@@@@=[0, 0]¾(([0, 99])[x:=x+1])=[0, 0]¾(([1, 100])=[0, 100]
@@ÆÈèAn101ÅÍX2(n)=[0, 100]ÆAs®_ÉB·éi±êªßéðjB
@ãLÌð@ð{¿ÌæPÍPDQßÌuÄAÆs®_vÌ_©ç®·éÆAÌæ¤ÉÈéG
iPjvOÌX2ðßé®ÍAºLÌæ¤ÉX2ÉÖ·éÄA®(zÂè`jÆÈÁÄ¢éB
@@@@X2=[0, 0]¾((X2¿[-, 99])[x:=x+1])@EEE@
iQj±êðð½ßÉAºLÌQ»®ðl¦½G
@@@@@X2(i+1)=[0, 0]¾((X2(i)¿[-, 99])[x:=x+1])@EEEA
iRjX2(0)=ÛiŬ³j©çoµÄiQjÌQ»®ÌlðßéÆA
@@ X2(1)=[0, 0]¾((X2(0)¿[-, 99])[x:=x+1])=[0, 0]¾(Û¿[-, 99])[x:=x+1])
@@@@@=[0, 0]¾(Û)[x:=x+1])=[0, 0]¾(Û)=[0, 0]
@@@X2(2)=[0, 0]¾((X2(1)¿[-, 99])[x:=x+1])=[0, 0]¾([0, 0]¿[-, 99])[x:=x+1])
@@@@@@=[0, 0]¾([0, 0])[x:=x+1])=[0, 0]¾([1, 1])=[0, 1]
@@@ÆÈèAX2(0)º X2(1)ºX2(2)ºEEEEºX2@@EEEB
·Èí¿Aß½¢X2ÍAP²ÁÌWñÌæiÉÀjÉ éB
±±ÅAX2(i)ðX2(i+1)Éγ¹éÖðFÆ·éÆA
@@@@@X2(i+1) =F(X2(i))@EEEC
@@@@@@@@i=[0, 0]¾((X2(i)¿[-, 99])[x:=x+1])j
@±ÌÖFÍAÄAvOð\·®X2ÌQ»®ãÌÖÅ èAFÌè`ÉÍàÍâÄAª»êÈ¢±ÆÉÓBFÍܽAÏxà\»ÉÜßéÆA
@@@@@FiX2(i))(x)=[0, 0]¾((X2(i)¿[-, 99])[x:=x+1]
@Å\»³êéB±êÍAX2(i) (x)ðÖÆ©½Æ«FÍÖðÏÆ·éÖiÖÌÖjÆl¦çêéÌÅiÄjÖÆ¢¤B
ܽAX2ªX2(i)ÌÉÀiX2(0)º X2(1)ºX2(2)ºEEEEºX2jÆ¢¤±ÆÍAX2(i)¨X2A@X2(i+1)¨X2
@@@@µ½ªÁÄAC®©çºLª¬§·éG
@@@@@@@@X2 =F(X2)
@±êÍAQ»®CÌðX2ªFÌs®_Å é±Æð¦µÄ¢éB
ÈãÍAÛðßžçê½®QÌð@i½ASYjÅ éªA±Ìð@ÉͺLÌâè_ª éB
yâè_zX2Ìlðßé½ßÉ101ñÌJèÔµvZªKv¾ªA±êðÈPÉoÈ¢©HܽAJèÔµñªLÀÅȢƫÍǤ·é©H±êÉηéð@ªÌßÌÛðßÌWideningÅ éB
QDR@s®_ß@EEEWidening
@WideningÍÛðßɨ¢ÄAvO©çìçê½®QððêAKvÈvZXebvÌðåɸçµÄŬs®_Ìßð¾é½ßÉgp·éBܽA³ÀñÌìðLÀÅÅ¿Øé±ÆªÅ«é½ßAvOðÍÌ®¹ðÛØ·éB±ÌßÍÊ¿i¶£UjÌWideningÌàeðSÉྷéiCousot_¶ÌuXß@s®_ß@vÌwideningƯlÌáÈÌÅjB
QDRDP@WideningZq
@(L,ºjð®õ©iÖWºÉÖµãÀAºÀª¶Ý·éjÆ·éB
ºLð½·Æ«AÞFL~L¨LªwideningZqÅ éÆ¢¤G
@@ÞÍãEZqÅ éB
@@@·Èí¿ACÓÌx, y¸LÉεÄAx¾yºxÞy
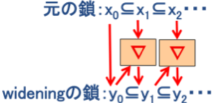
@ALÀ½(Chain)Ìð
@@ LÌP²å·é½ x0ºx1ºEEEºxnEEEÉεÄA
@@ ÞZqÉæé½@
@@@@@@y0=x0, y1=y0Þx1, y2=y1Þx2,EEE, yn+1=ynÞxn+1,EEE
@@@ÍALÀÅÀè·éiåªLÀñÅ~ÜéjP²å½Å éB·Èí¿A
@@@½émª¶ÝµÄA0ºy1ºEEEºym=ym+1=ym+2=EEE
·Èí¿A³À̽(xn)ÉεÄAwideningZqÞÉæèLÀÅÀè·é½(yn)ªè`³êéB
@@@@
¡windeningZqÌá
@ æÔÌWÉεÄwideningZqðȺÌæ¤Éè`·é
@@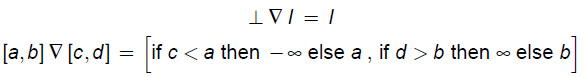
±ÌÆ«AÞÍwideningZqÌðð½·G
@(xn)FÛº[0, 0]º[0, 1]º[0, 2]ºEEEE
@ÉεÄAy0=Û, y1=y0Þx1=ÛÞ[0, 0]=[0, 0], y2=y1Þx2=[0, 0]Þ[0, 1]=[0,],
@@@@@@@@@y3=y2Þx3=[0,]Þ[0, 2]=[0,]
@ÆÈèA(yn)FÛº[0, 0]º[0,]=[0,]EEE
@·Èí¿ALÀñi3ñjÅ[0,]Éû©·éB
QDRDQ@Ûðßžçê½®QÌWideningÉæéð@iáPj
@OÅè`µ½æÔÌwidenigZqðQDQDSÌ®QÉKp·éÆAºÌæ¤É3ñÅû©·éB
@@
¡ãLÌwideningÌ®Ìà¾
@@@wideningOÌP²å·é½i`FCjͺLG
@@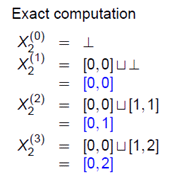
@@AãL½Éηéwidening̽ðßéG
@@@@wideningÌX2(0)=³Ì½ÌX2(0)=Û
@@@@wideningÌX2(1)= wideningÌX2(0)޳̽ÌX2(1)=ÛÞ([0,0]¾Û)=ÛÞ[0,0]
@@@@wideningÌX2(2)= wideningÌX2(1)޳̽ÌX2(2)= [0,0]Þ([0,0]¾[1,1]))
@@@@@@@@@@@@@@@@@@= [0,0]Þ[0,1]=[0,]
@@@¯lÉAwideningÌX2(3)=[0,]ÆÈèAû©·éB
@@@]ÁÄAwideningÌX2(i)ðX2(i)Æ·éƺÌʪÜéB
@@@
@@BwideningÉæèX2(2)=[0,]Éû©µ½B
@@@@±Ìlð®@X2(i+1) = [0, 0]¾((X2(i)¿[-, 99])[x:=x+1])
@@@@Éãü·é±ÆÉæèALÀÌs®_ÉB·éB±ÌvZXðDescending sequenceÆ¢¤B
@@@
@±êÍ]Ìè@Ì101ñÌJèÔµvZƯ¶ÊÆÈÁÄ¢éB
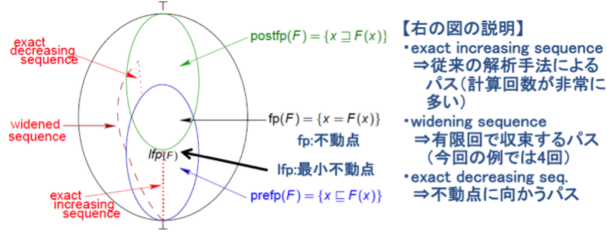
QDRDR@WideningÉæéð@iáPjÌÜÆß
@@wideningZqÆdescending sequenceÉæèAu]ÌðÍè@ÅÍ101ñvµÄ¢½vZª
@í¸©4ñÅßé±ÆªÅ«½ijBv@±êÍWideningÌÐÍiwÇvZ¹¸ÉÊð¦·jB
@ij±ÌáÍPÈÌů¶ð[0, 100]ª¾ç꽪êÊÉͳmÈðæèÍL¢ßðÆÈéB
@@@
@@@@@@@@@@@}QDQQ@WideningZÌà¾
@@ܽAWideningÉæéû©vZÌOt\»ÆdescendingÌÓ¡É¢Äl¦ÄÝéB
@@@@@@@@@@X2(i+1)=F(X2(i))=[0, 0]¾((X2(i)¿[-, 99])[x:=x+1])
@Æ·éÆ«A±êÌWideningÉæéû©vZÍ}QDPUÌæ¤É\»³êéiQl¿TÌXChð³Éì¬jG
@@@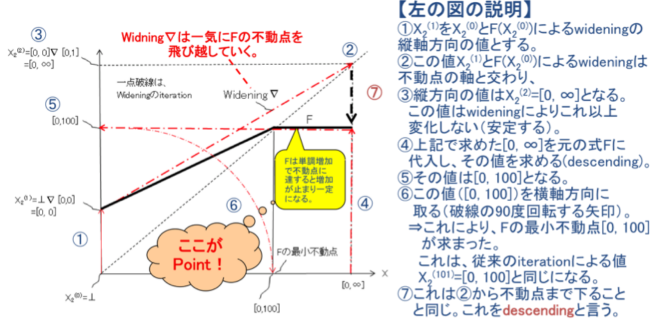
@@@@@@@@@}QDQR@WideningÉæéû©vZÌOt\»
QDRDS@Ûðßžçê½®QÌWideningÉæéð@iáQFZero divideÌÂ\«Ìáj
@ºLÌæ¤ÈPÈvOðáɵÄȺÌâèðÝèµAðÍðsȤBËPolyspace TechnologiesÌXChÅÐî³ê½áB
yâèzºLÌvOÅZero divideª¶·é©H
@@@
@±êðÊíÌfobOÅmF·éÆAKÌæè¾élªL¢ÌÅ©ÈèèÔª©©éB
@@PolySpaceÌ¿ÅÍA®ÆŬs®_Éæéðª éBËÇÌæ¤ÉµÄ±©êé©Æ¢¤vZßöÍ©êÄÈ¢B
@@
@È~A±Ì®Ì±oßöðྷéB
Ïi,j,kÌæè¾éÍÍÉ Ú·éÆAvOÌeXebvÌӡͺLÌæ¤ÉÈéB
@@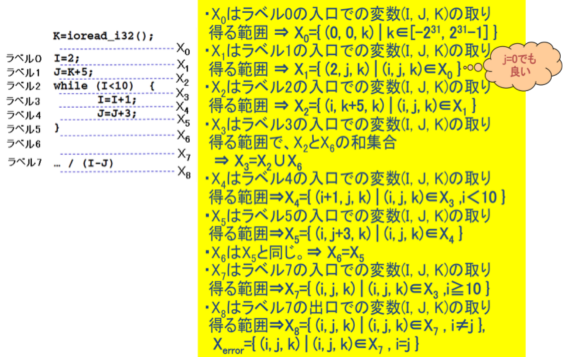
·Èí¿AvOÌ®\»ÍºLÌEÌæ¤ÉÈéB
@@
@ɱêðuJIXIJèÔµ@vÆuwideningZ@vÌQÂÅð¢ÄÝéB
iPjJIXIJèÔµ@Éæéð@
@@ãÅß½®ðX1©çÉãüµÄÅãÌX8ðßéG
@@ X0={ (0, 0, k) | k¸[-231, 231-1] }ðX1Éãü·éÆA
@@@X1={ (2, j, k) | (i, j, k)¸X0 }={ (2, 0, k) | k¸[-231, 231-1] }
@A ãÅß½X1={ (2, 0, k) | k¸[-231, 231-1] }ðX2Éãü·éÆA
@@ @@X2={ (2, k+5, k) | k¸[-231, 231-1] }
@ãLÌQÂÍÈPÉßç꽪AÌX3Íû©vZªKvÆÈéG
@B ãÅß½X2={ (2, k+5, k) | k¸[-231, 231-1] }ðX3Éãü·éÆA
@@@X3=X2¾X6={ (2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i, j, k)¸X4 }
@@@@@@@= {(2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i-1, j, k)¸X3 , i10 }
@@·Èí¿AX3ÌÝðÏÆ·éÄA®ªßçê½G
@@ X3= {(2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i-1, j, k)¸X3 , i10 }
@ ±êðX3ÌŬ³©çnßÄP²å·éºLÌQ»®ÉæèAX3ÌlÌÍͪ¦ÈÈéÜÅ
@@JèÔµvZ·é(Ŭs®_vZjG
@@@X3(n+1)= {(2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i-1, j, k)¸X3(n) , i10}
@@±ÌQ»®ÉæéŬs®_vZðºLɦ·B
@@@X3(n+1)= {(2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i-1, j, k)¸X3(n) , i10}@EEE(1)
@@±Ì(1)®ðnÉ¢ÄÌQ»®ðŬ³ióWj©çoµÄð¢Ä¢G
@@n=0ÌÆ«AX3(0)=ÓióWj
@@±êð(1)®Éãü·éÆA
@@X3(1)={(2, k+5, k) | k¸[-231, 231-1] }¾Ó={(2, k+5, k) | k¸[-231, 231-1] }
@@±êðÄÑ(1)®Éãü·éÆA
@@X3(2)={(2, k+5, k) | k¸[-231, 231-1] }¾{(i, j+3, k) | (i-1, j, k)¸X3(1) , i10}
@@@@@={(2, k+5, k) | k¸[-231, 231-1] }¾{(3, k+5+3, k) | k¸[-231, 231-1] , i10}
@@@@@={(i, j, k) | k¸[-231, 231-1], i¸[2, 3],@j=k+5Íj=k+5+3}EEE(2)
@@±±ÅAj=k+5Íj=k+5+3ÍÌæ¤Él¦éG
@@j=k+5=k+3*2-1, j=k+5+3=k+3*3-1·Èí¿Ai=2, 3ÌÆ«Aj=k+3*i-1ÆZßçêéB
@@µ½ªÁÄA(2)ÍÌæ¤ÉÈéG
@@X3(2)={(i, j, k) | k¸[-231, 231-1], i¸[2, 3],@j=k+3*i-1}
@@ȺA¯lÉJèÔµvZµÄ¢ÆA
@X3(9)={(i, j, k) | k¸[-231, 231-1], i¸[2, 3, 4,EEE, 10],@j=k+3*i-1}@EEE(3)
@X3(10)=X3(9)ÆÈèA(3)ªX3ÌŬs®_Å é±Æªª©éB
@@·Èí¿A
@@X3={(i, j, k) | k¸[-231, 231-1], i¸[2, 3, 4,EEE, 10],@j=k+3*i-1}
@@ @={(i, j, k) | k¸[-231, 231-1], i¸[2, 10], j=k+3*i-1}@@@i[2, 10]ÍæÔð¦·j
@CÉX3={(i, j, k) | k¸[-231, 231-1], i¸[2, 10], j=k+3*i-1}ðX4ÌEÓÉãü·é±ÆÅX4Ìlð
@@ßéG@X4={ (i+1, j, k) | (i, j, k)¸X3 ,i10}@EEE(4)
@@±±ÅAX3ÌiÍX4ÅÍi+1Éu«·¦çêÄ¢éÌÅAX4Ìi+1ðiÅ\»·éÆA
@@X3ÌiÍi-1ÆÈéG i-1¸[2, 10]¨i¸[2+1, 10],@j=k+3*(i-1)-1
@@µ½ªÁÄA(4)ÍÌæ¤ÉÈéG
@@X4={(i, j, k) |@k¸[-231, 231-1], i¸[2+1, 10],@j=k+3*(i-1)-1}
@@@@={(i, j, k) |@k¸[-231, 231-1], i¸[3, 10],@j=k+3*i-4}
@D¯lÉAX4 ={(i, j, k) |@k¸[-231, 231-1], i¸[3, 10],@j=k+3*i-4}ðX5ÌEÓÉ
@ @ãü·é±ÆÅX5ÌlðßéG
@@@@X5={ (i, j+3, k) | (i, j, k)¸X4}@EEE(5)
@@±±ÅAX4ÌjÍX5ÅÍj+3Éu«·¦çêÄ¢éÌÅAX5Ìj+3ðjÅ\»·éÆA
@@X4ÌjÍj-3ÆÈéG@j-3=k+3*i-4¨j=k+3*i-1
@@µ½ªÁÄA(5)ÍÌæ¤ÉÈéG
@@X5 ={(i, j, k) |@k¸[-231, 231-1], i¸[3, 10],@j=k+3*i-1}
@EX6=X5
@F¯lÉA X3 ={(i, j, k) | k¸[-231, 231-1], i¸[2, 10],@j=k+3*i-1}ðX7ÌEÓÉãü·é±ÆÅ
@@X7ÌlðßéBi=10ÈÌűêðãü·éÆA
@@X7={ (i, j, k) | (i, j, k)¸X3,i10 }
@@@@={(10, j, k) |@k¸[-231, 231-1], j=k+3*10-1=k+29}
@G¯lÉA X7 ={(10, j, k) |@k¸[-231, 231-1], j=k+29}ðX8ÌEÓÉãü·é±ÆÅX8Ìlð
@@ßéBX8ÉB·é½ßÉÍijÈÌÅA
@@X8={ (i, j, k) | (i, j, k)¸X7 ,ij }
@@@@={(10, j, k) |@k¸[-231, 231-1], j=k+29, ij }@EEE(6)
@ÈãÉæèAPolySpaceÌ¿ÌŬs®_Éæéðªßçê½B
ÉAÅãÌ®(6)ÌÓ¡ðl¦éG
@@@X8={(10, j, k) |@k¸[-231, 231-1], j=k+29, ij }@
±Ì®©çAj=10ÌÆ«i=j=10ÆÈèAvOÍxVɨ¢ÄZero divide
ª¶·é±Æªª©éBܽA±ÌÆ«Ìk=-19Å éB
iQjWideningÉæéð@
¡ºLÌ(1)®ðwideningÅðB
@X3(n+1)= {(2, k+5, k) | k¸[-231, 231-1] }¾{ (i, j+3, k) | (i-1, j, k)¸X3(n) , i10}@EEE(1)
ãL(1)®Í(i, j, k)Æ¢¤RÏÌ®¾ªAk¸[-231, 231-1]ͱêÈã»ÌlÌÍͪg幸A j=k+3*i-1©çjÍi, kÉæèêÓIÉÜéÌÅAwideningƵÄgå·é½ÍiÉ¢ÄÌÝl¦éB·Èí¿APÏæÔÉæéwideningÅÎÅ«éijB
@@@@@@@@@@@@@@@@@
ȺA»Ìèð¦·G
@wideningOÌP²å·é½ÌÅÌðl¦éi±êÍA4.2(4)ÅvZÏj
@@@X3(0)=ÓióWj
@@@X3(1)={(2, k+5, k) | k¸[-231, 231-1] }
@@@X3(2)={(i, j, k) | k¸[-231, 231-1], i¸[2, 3],@j=k+3*i-1}
@±±ÅAiÌÝÉ¢Ä̽ðl¦éBiÉ¢Ä̽Í
@@@[X3(0)]i =ÓA[X3(1)]i =[2, 2]A[X3(2)]i =[2, 3]@@
AãLÌiÉ¢Ä̽ÉεÄwidening̽ðßéG
@@@widening̽Ì[X3(0)]i =³Ì½Ì[X3(0)]i =ÓA
@@@widening̽Ì[X3(1)]i =(widening̽Ì[X3(0)]i)Þ(³Ì½Ì[X3(1)]i) =ÓÞ [2, 2]=[2, 2]
@@@widening̽Ì[X3(2)]i =(widening̽Ì[X3(1)]i)Þ(³Ì½Ì[X3(2)]i) =[2, 2]Þ[2, 3]=[2,]
@@@@@EEE±êÈãiÍgåµÈ¢ÌÅwideningÍû©I
µ½ªÁÄAwideningÅß½X3(n)Ìû©lÍ
@@X3(2)={(i, j, k) | i¸[2, +], k¸[-231,231-1], j=k+3*i-1}EEE(2)
ÆÈèA±êð(1)®Éãü·éÆA
X3(3)= {(2, k+5, k) | k¸[-231, 231-1]@}¾{(i, j+3, k) | (i-1, j, k)¸X3(2) , i10}EEE(3)
±±ÅA (3)®Ì{(i, j+3, k) | (i-1, j, k)¸X3(2) , i10}Ì
Ïiªæè¾élÍA(2)®æèi-1¸[2, +] & (i10)æèAi-1=2, 3, 4, 5, 6, 7, 8, 9
@@@Ëi=3, 4, 5, 6, 7, 8, 9, 10@·Èí¿Ai¸[3, 10]
ÏjÌlÍA (i-1, j, k)¸X3(2)æèAj=k+3*(i-1)-1@Ëj+3=k+3*(i-1)-1+3=k+3i-1
±êÉæèA{(i, j+3, k) | (i-1, j, k)¸X3(2) , i10}
@@={(i, J, k) | k¸[-231,231-1], i¸[3, 10], J=k+3*i-1}
µ½ªÁÄA(3)®ÍA
X3(3)= {(2, k+5, k) | k¸[-231, 231-1] }¾{(i, J, k) | k¸[-231,231-1], i¸[3, 10],@
@@@@@@@J=k+3*i-1} ={(i, J, k) | k¸[-231, 231-1], i¸[2, 10],@J=k+3*i-1}
ÆÈèAQDRDSiPjÌJèÔµvZƯ¶Êª¾çê½BiÊíÌvOðÍÅÍ10ñÌJèÔµ
ªKv¾ªAwideningÅÍ2ñÅû©Ij
ËWideningÍvOÌ[vðêCÉð·éè@B
@@@@@@@@@@@@@@
QDRDT@WideningÌÜÆß
iPjOÒär
@@@@@@
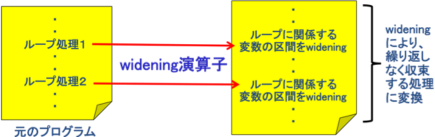
iQjWideningZqÌRZvgG
@E±ÌZqÍ[v/TCNÌPÂÌCe[VãÌóÔÌÏ»ð²×A¯¶Ï·ª³Àñ
@ N«é©àµêȢƼèµÄA±Ìîñ©ç[vÌU¢ðO}µæ¤Æ·éB
@E±ÌZqÍ[vÌJèÔµªiÌlð峹Ģé±ÆðmµA»êª³ÀñN«é±Æð
@O}·éB±ÌO}ÍT¦Ú߬é©àµêÈ¢ªªÍÌ®¹ðÛØ·éB
@@@@@@@@@@@
@