第３章　初期論文以降の展開と抽象解釈考

３．１　初期論文以降の展開　

　本資料で説明した初期論文のその後の展開については、各章で[最近の論文からの注釈]という形式で部分的に補足してきた。ここでは、初期論文が「抽象解釈のプログラム変数が１変数という非常に単純な場合しか具体例が示されていなかったので、プログラム変数が多変数の場合についてのその後の展開を簡単に示す。

まず、プログラムの扱う変数が２変数の場合、最も単純な領域としては矩形（直積領域）が考えられる。

　（例）0≦x≦1,0≦y≦1のとき、(x, y)の存在領域は[0,1]×[0,1]

　　　　

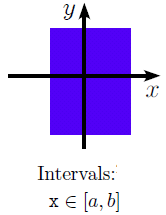
　　　　　図３．１　直積領域

　しかし、これはx,yがお互いに全く関係のない変数の場合は良いが、x,yに何らかの関係がある場合（プログラムの値が例えばxとyの関係式x/(x-y)で表される場合など）、２変数の取り得る値の範囲としては粗過ぎる。例えば、序論の２．１の説明で使った図で説明すると、zero divideを示す禁止ゾーンの直線と矩形の領域は重なっているので、矩形による判定では「zero divideの可能性有」となる。しかし実際の値（図の×印）ではzero divideは発生しない。矩形の領域を多角形に替えるとzero divideが発生しないことが分かる。

　　　　

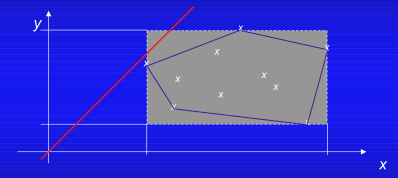
　　　　図３．２　領域によるzero divideの可能性の判断

　このように、P. Cousotはプログラム変数が多変数の場合を検討し、1978年に下記の論文で多変数のプログラムの変数間に関係がある場合、多面体近似による抽象解釈モデルを考えた；

P. Cousot and N. Halbwachs： Automatic Discovery of Linear Restraints Among Variables of a Program

　これは、下記のようにプログラムの変数を、変数間の不等式に自動的に変換することを用い、それらの不等式群が作る多面体領域で抽象解釈の議論（多面体のwideningなど）を行うという考えである。

　　

　　　　　　　図３．３　プログラム変数の不等式変換例

（例）解析対象のプログラムが２変数x,yでその関係が一次式ならば、変数の取り得る領域は一次不等式a≦x±y≦bで多角形の領域。

　　　　

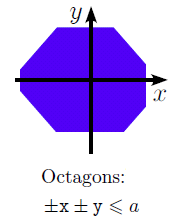
　　　　　図３．４　多角形領域

　この方法はその後さらに進んで、解析対象のプログラムが２変数x,yでそれらの関係が二次の関係式、例えば、x²+by²-axyならば、変数の取り得る領域はx²+by²-axy≦dで表され、これは楕円の領域となる、などというように緻密に扱われるようになった。

　　　　

　　　　　　図３．５　楕円領域

　抽象解釈では、プログラムの変数の個々の値を考えるのではなく、変数の取り得る値を含む領域を考えるので、（複雑さとのトレードオフの問題でもあるが）その領域は出来るだけ変数の取り得る領域に近いものがよい。

　ここで一つ注意すべき点（健全性と安全性）がある。抽象解釈では変数の取り得る値を含む近似領域を考えることにより、プログラムの変数の禁止ゾーンとそれが交差しないことが真であることを証明しようとしている。しかし、それが偽の場合、実際のプログラムが誤りとは限らないことである。例えば、下の図でzero divideとなる禁止ゾーンx=yと多角形は交差しているので、抽象解釈では「zero divideは発生しない」という命題は否定される。すなわち、「zero divideの可能性有」ということしか分からない。

　　　　

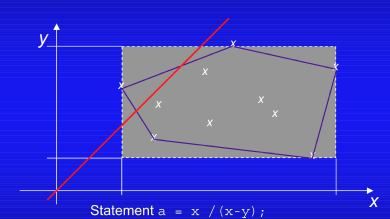
　　　　　図３．６　領域によるzero divideの可能性の例

　検証したいこと（例ではプログラムがZero divideを発生しないこと）が真であることが保証されることを健全性(soundeness)という。抽象解釈の場合、健全性は保証されるが、検証したいことが偽の場合は可能性までしか分からない。この場合、正確さは失われているが、偽の可能性を指摘しているという点で安全サイドの結果である。

　以上は抽象解釈の考え方であるが、これを搭載した静的解析ツールは、欧米で商用化されていて(Polyspace等）プログラム解析に威力を発揮している。PolySpace自体は1996年にフランスの研究機関によって実用化され、日本でも2001年から販売されている実績のあるツール。導入事例としては、航空宇宙・防衛、自動車、産業装置、交通・運輸、家電製品、医療機器など多岐に渡る。

　　　　

　　　　　図３．７　PolySpaceの特徴

３．２　抽象解釈考：ガロア理論との対比

　抽象解釈ではガロア接続というガロアの名前が登場する。下記に抽象解釈の特徴とガロア理論を対比し両者の類似性を考えてみる；

　　　　

　　　　　図３．８　抽象解釈とガロア理論の類似性

扱う対象は異なるが両者に共通していることは、

「対象の難しさに正攻法で正面から力ずくで攻めるのではなく、その対象の『或る構造（注）』を抽象化し、そこで問題を解くことである。」

　（注）着目する視点；

　　　　・抽象解釈の場合は、プログラムの変数の値の単調増加性という『束の構造』であり、

　　　　・ガロア理論の場合は、方程式の解の持つ『対称性の構造（体と群の構造）』である。

　　これを図で比較すると、次頁のようになる。

　　　　

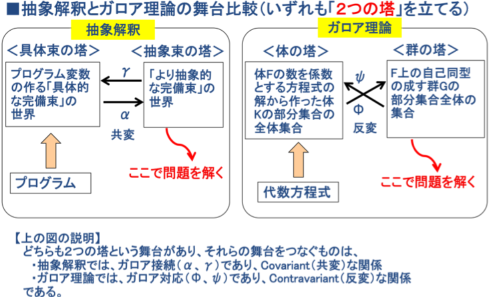
　　　　図３．９　抽象解釈とガロア理論の舞台比較

　次に、抽象解釈の難しさについて考えてみる；

　 ガロア理論の特徴は、方程式を計算で解くというそれまでの代数学を根底から変えて、体や群と

　いった抽象度の高い数学的「構造」を議論していることにある。これは、高校までの「計算＝数学」

　という考えに馴染んでいた人にとっては思考のコペルニクス的転換が必要になる。　

　 同様のことが抽象解釈にも言えるのではないか。

　すなわち、プログラムを一行、一行実行するという従来の考えを根底から変えて、プログラムの変数

　が作る束という数学的「構造」で考えるということである。

（参考）上記のような構造はモデル検査の抽象化においても見られる。

　すなわち、Kripke構造間の抽象化写像βを作ることができれば、「単純化された抽象構造」で問題

　を解くと、それが元の複雑な構造の解となる。」ということが成立する。そのしくみは、C,Aから作られ

　るベキ集合の世界で、βを元に写像α、γを作ると、これがガロア接続となり、不動点定理適用により

　上記が成立することが証明される。

　　　　　　

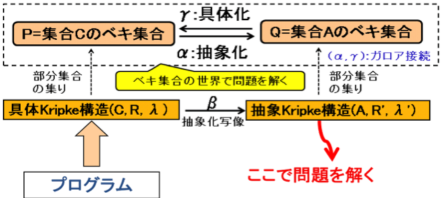
　　　　　　　図３．１０　モデル検査の抽象化

文献

１．P.Coust and R.Cousot: A unified lattice for static analysis of　programs by construction or approximation of fixpoints (1977)　⇒本資料で「Cousot初期論文」としたもの。

２．A. G. Parameswaran: Abstract Interpretation for Model Checking,　B. Tech. Seminar Report, Indian Institute of Technology, Bombay, 2006　⇒上記No.1の論文に沿った説明がなされている。

３．Flemming Nielson, Hanne Riis Nielson, Chris Hankin; Principles of Program Analysis, Springer 2005

⇒プログラム解析と抽象解釈について書かれた専門書（大学院生向けのテキスト用）。本資料では、

　第4章のガロア接続の部分を使用。

４．Klaus Denecke, Marcel ErnÉ, Shelly L. Wismath. Galois connections and applications (Mathematics and Its Applications), Springer, 2004

⇒ガロア接続の話題を1冊に纏めた数学とその応用の専門書（大学院生または研究者向け）。理工学だけでなく、人文系含めた様々な分野にその概念が適用されていることが分かる。本資料では、補足IIの「ガロア接続の由来」に使用。

５．P. Cousot: Formal Verification by Abstract Interpretation, at 4th　NASA　Formal　Methods　Symposium(2012)　⇒２．２．４節の「符号の規則」の説明に使用した。

６．Nicolas Halbwachs, On the design of widening operators

　　Verimag/CNRS. Grenoble,　Invited Tutorial　at VMCAI 2006 (*)

　(*)Verification, Model Checking, and Abstract Interpretation, 7th International Conference

⇒２．３節のWideningの説明に使用した。

７．Chris Hote, Abstract Interpretation Appliedto Static Run-Time Error Detection (SigAda 2002)

⇒２．３節のWideningの説明に使用した。

８．E. GALOIS, MÉMOIRE　SUR LES CONDITIONS DE RÉSOLUBILITÉ DESÉQUATIONS PAR RADICAUX（根号により方程式が解けるための条件について）, 1831

⇒今日、ガロア第I論文と呼ばれるものである。本資料では、ガロア理論との対比に使用。

９．横内寛文、プログラム意味論、共立出版、1994

⇒１．２節の再帰と不動点の説明に使用した。

１０．Patrick Cousot, Abstract Interpretation: Achievements and Perspectives, DÉpartement d'informatique,École normale supÉrieure) ,　Technique et science informatiques. Vol. 19 - n0 1/2000,

⇒[最近の論文からの注釈]として使用した。

１１．　D. Schmit, All the world is an abstract interpretaion ( of all the world), Kansas State University

⇒簡単な図やプログラム例で初めての人向けに抽象解釈の説明をしている。