単純なプログラム例による抽象解釈入門
(Cousot初期論文(*)を読む)
(*)ABSTRACT INTERPRETATION: A UNIFIED LATTICE MODEL FOR STATIC ANALYSIS OFPROGRAMS BY CONSTRACTION OR APPROXIMATION OF FIXPOINTS(抽象解釈:不動点
近似によるプログラムの静的解析のための統一束モデル)
By Patrick. Cousot and Radhia Cousot [1977年]
2013年10月Ver.1.0 作成 舟越 和己
目次
序論
1.本資料の目標
2.抽象解釈とその歴史
3.Cousot初期論文とは何か
4.本資料の構成
第1章 準備
1.1 半順序集合と束
1.2 再帰と不動点
1.3 ガロア接続
第2章 抽象解釈概要(主にCousot初期論文から)
2.1 プログラムの意味論と抽象解釈の基本用語(論文の第3節と第4節)
2.2 プログラムの抽象解釈(論文の第5節~第8節)
2.3 不動点近似法(Widening:文献6より)
第3章 初期論文以降の展開と抽象解釈考
3.1 初期論文以降の展開
3.2 抽象解釈考:ガロア理論との対比
第1章の準備からから第2章までのステップを登山に喩えると、・・・

序論
1.本資料の目標
「抽象解釈」についての文献は海外には多数あるが論文など専門的な内容が多く、プログラム意味論や完備束などかなりの予備知識がないと理解できないものが大多数である。また、抽象解釈について日本語で書かれた平易な解説資料は殆どないのが現状である。
本資料は、抽象解釈を理解するための必要最小限の知識を第1章で準備し、非常に単純なプログラム例(下記)を使って抽象解釈の基本的概念を抽象解釈の古典とも言えるCousotの初期論文に沿って解説することを目標とする。単純なプログラム例では抽象解釈の威力が伝わり難い部分があるかもしれないが、ここでは抽象解釈の仕掛けを出来るだけ平易に伝えることを主眼とした。
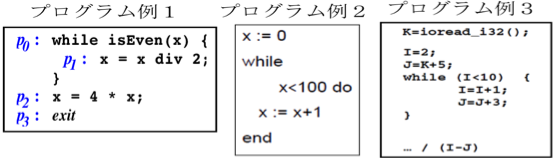
2.抽象解釈とその歴史
2.1 抽象解釈とは
現実のプログラムは変数や状態数が非常に大きいことなどがあり、その解析は非常に困難である。抽象解釈はこれに対する一つの解決法を示している。
P.Cousotの言葉によれば、「抽象解釈はソフトウェアの解析と静的検証に主に使用できる情報システムのセマンティクス(意味論)についての離散的な近似の理論」である。もっと簡単に言えば、プログラムの解析に必要な側面に着目してそれをモデル化(プログラムのセマンティクス)することにより、プログラムを実際に実行することなく、全ての可能なプログラム結果を含む安全な近似解を求める手法である。
簡単な例で説明すると、x/(x-y)というzero divideの可能性のある式を含むプログラムをチェックする場合、下の図のように抽象解釈では、プログラムの変数の個々の値(図では×の記号)を考えるのではなく、全ての取り得る値を含む近似領域(図では多角形の領域)を考える。そして、この多角形領域がプログラム変数の存在を禁止されているゾーン(図ではzero divideを示す直線y=x)と交差していないかをチェックすることにより、プログラムの検証を行うという考え方である。この図の場合、交差していないので確実にzero divideは発生しないことが保証される。これは、プログラムの変数に着目したモデル化である。
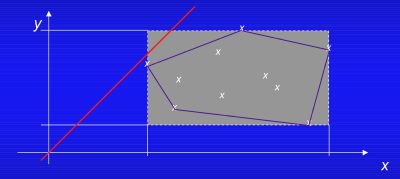
ここには、プログラムの動きを幾何学的に見て判断するという発想の転換が見られる。ここで重要なことは、プログラム変数の可能な存在領域をどのようにして近似するかということである(本資料でもこの説明が大半を占めている)。抽象解釈はこの問題に答えるために、プログラム意味論の上に完備束や不動点定理及びガロア接続などの数学的議論を展開している。この意味で、抽象解釈はソフトウェアの世界に近代数学が適用された数少ない成功事例の1つである。
例えば、不動点定理やガロア接続が抽象解釈においてどのように関係するかをざっくりと紹介する:
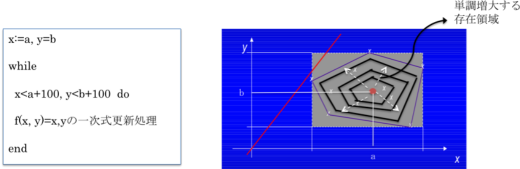
下記の例でプログラムの変数(x,y)の存在領域がプログラムの再帰処理により下の図のように単調増大しているとする。このとき、プログラム変数の可能な存在領域を求めることは、その領域がこれ以上増大しない、すなわち不動領域を求めることで得られる。単調増大領域の極限は一般的には漸化式で求まるが、抽象解釈ではこれを一気に求める手法も考えられている(Widningなど)。変数の値の存在領域は、意味のある範囲で単純な方が良い。抽象解釈では、ガロア接続はこのような単純な領域への対応関係として位置付けられる。
2.2 抽象解釈の歴史
抽象解釈の手法が提案されたのは1970年代初めの頃。フランスのP. Cousot, R. Cousot(注)などによりその基礎が確立された。現在では、高度な静的解析ツール(PolySpace, AstrÉeなど)やモデル検査などにその手法が応用されている。
(注)Patrick Cousot:パリのÉcole Normale SupÉrieure(高等師範学校)情報学部教授
Radhia Cousot:Directrice de recherche CNRS &École Normale SupÉrieure

École Normale SupÉrieure(エコール・ノルマル・シュぺリウール)はフランスの高等教育機関(グラン
ゼコール)の一つ。著名な哲学者(サルトル他)、文学者(ロマン・ロラン他)、数学者などを多数輩出。
CNRS:Le Centre national de la recherche scientifique(フランス国立科学研究センター)1939年設立
3.Cousot初期論文とは何か
本資料で言う「Cousot初期論文」とは下記の論文を指すものとする。
Patrick. Cousot and Radhia Cousot , ABSTRACT INTERPRETATION: A UNIFIED LATTICE MODEL FOR STATIC ANALYSIS OF PROGRAMS BY CONSTRACTION OR APPROXIMATION OF FIXPOINTS(抽象解釈:不動点近似によるプログラムの静的解析のための統一束モデル), 1977年
上記の論文の目次は次のようになっている;
1.序論
2.要約
3.プログラムの構文論と意味論
4.プログラムの静的意味論
5.プログラムの抽象解釈
6.一貫した抽象解釈
7.抽象解釈の束
8.プログラムの抽象評価
9.不動点近似法・・・Widening/Narrowing
10.結論
【論文で使用される主なキーワード】
プログラムの構文論と意味論、半順序、束、擬順序、半束、完備束、再帰式と不動点、
タルスキの不動点定理、クリーネシーケンス、データフロー解析、ガロア接続、ガロア挿入、
コンテキスト、コンテキストベクトル、Widening/Narrowing
目次から分かるように、この論文にはプログラム意味論・束論・不動点定理・Widening/Narrowingなど抽象解釈の基本的概念が全て登場している。その意味では、「抽象解釈の古典」として現在でも読む価値のある論文である。しかし、内容はかなり難しく論文を日本語に訳すだけでは不十分であり、これを読むためのポイントを絞った解説が必要となる。このため本資料では、この論文の主な内容を簡単な例等で説明するスタイルを取ることにする。但し、論文の「9節 不動点近似法」は別資料(文献6)で説明する。
また、抽象解釈のその後の進展により、初期の論文の考え方はセマンティクスの抽象モデルとして整理され、定式化されたので、[最近の論文からの注釈]を付けて抽象解釈の現代的な概念や表現との対応も示すようにした。
4.本資料の構成
本資料は下記の構成となっている。
第1章 準備 (1.1~1.3)
第2章 抽象解釈概要 (2.1~2.3)
第3章 初期論文以降の展開と抽象解釈考 (3.1、3.2)
文献
第1章の準備は本論の第2章を読むために必要な基本的概念の導入であり、何れの節にも必須の内容である。