ƒvƒچƒOƒ‰ƒ€‚ج“®“Iگ«ژ؟‚جگأ“IŒˆ’è(STATIC DETERMINATION OF DYNAMIC PROPERTIES OF PROGRAM)پ@
Patrick. Cousot and Radhia Cousot :ƒOƒ‹ƒmپ[ƒuƒ‹—‰بˆم‰ب‘هٹwڈî•ٌŒ¤‹†ڈٹ(Laboratoire d'Informatique, Universite Scientifique et Medicale de Grenoble)پ@: 2nd Int. Symposium on Programming, Paris [1976”N]
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‚Q‚O‚P‚S”N‚PŒژپ@“ْ–{Œê–َ‚ئ‰ًگàچىگ¬پFڈM‰zپ@کaŒب
‚PپDڈکک_(Introduction)
پ@چ‚‹‰Œ¾Œê‚ة‚¨‚¢‚ؤپAƒRƒ“ƒpƒCƒ‹ژ‚جŒ^Œںڈط‚حٹ®‘S‚إ‚ح‚ب‚پA“®“I‚بƒ`ƒFƒbƒN‚ھ‘خڈغ‚جƒRپ[ƒh‚ةچs‚ي‚ê‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB—ل‚¦‚خپAPASCAL‚إ‚حƒTƒuƒŒƒ“ƒWƒ^ƒCƒv‚ج•دگ”‚â“Yژڑژ®‚ة‘م“ü‚³‚ꂽ’l‚ھ‚Q‚آ‚جƒoƒEƒ“ƒ_ƒٹٹش‚ة‚ ‚邱‚ئ‚âپAƒ|ƒCƒ“ƒ^پ[‚ھnull‚إ‚ب‚¢‚±‚ئ‚ً“®“I‚ةŒںڈط‚µ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB
پ@‚±‚جک_•¶‚إ‚حپA‚±‚ê‚ç‚جڈط–¾‚ج‘½‚‚ًƒRƒ“ƒpƒCƒ‹ژ‚ةچs‚¤‚±‚ئ‚ً‰آ”\‚ة‚·‚éˆê”ت“I‚بƒAƒ‹ƒSƒٹƒYƒ€‚ً’ٌژ¦‚·‚éپB‰نپX‚ھچs‚¤ƒvƒچƒOƒ‰ƒ€‚جگأ“I‰ًگح‚حƒvƒچƒOƒ‰ƒ€‚ج’ٹڈغ•]‰؟‚©‚çگ¬‚èپA‚»‚ê‚حALGOL60‚جژ®‚جŒ^‚ًŒںڈط‚·‚邽‚ك‚ةNAURپi–َ’چ‚Pپj‚ة‚و‚èژg—p‚³‚ꂽ•û–@پAƒ‚ƒWƒ…پ[ƒ‹‚ئ‚»‚جک_—ژd—l‚ج‘خ‰‚ًŒںڈط‚·‚邽‚ك‚ةSINTZOFFپi–َ’چ‚Qپj‚ة‚و‚èژg—p‚³‚ꂽ•û–@پAƒvƒچƒOƒ‰ƒ€‚جگ«ژ؟‚ً’ٹڈo‚·‚邽‚ك‚ةWEGBREITپi–َ’چ‚Rپj‚ة‚و‚èژg—p‚³‚ꂽ•û–@پAƒvƒچƒOƒ‰ƒ€‚ج•دگ”ٹش‚جƒAƒtƒBƒ“ٹضŒW‚ًŒ©‚آ‚¯‚邽‚ك‚ةKARRپi–َ’چ‚Sپj‚ة‚و‚èژg—p‚³‚ꂽ•û–@پA‹y‚رSETLپi–َ’چ‚Tپj‚إ‚جژ©“®ƒfپ[ƒ^چ\‘¢‘I‘ً‚ج‚½‚ك‚ةSCHWARTZپi–َ’چ‚Uپj‚ة‚و‚èژg—p‚³‚ꂽ•û–@‚ة—قژ—‚µ‚ؤ‚¢‚éپB
پ@پ@پi–َ’چ‚PپjPeter Naur(1928-)‚حƒfƒ“ƒ}پ[ƒN‚جŒvژZ‹@‰بٹwژز‚إ‚ ‚èپAƒ`ƒ…پ[ƒٹƒ“ƒOڈـژَڈـژزپB
پ@پ@پ@پ@پ@پ@پ@ƒoƒbƒJƒXپEƒiƒEƒA‹L–@پiBNF notationپFBackus-Naur form)‚ة–¼‘O‚ھژg‚ي‚ê‚ؤ‚¢‚éپB
پ@پ@پi–َ’چ‚QپjMichel Sintzoff (12 Aug 1938 - Nov 28, 2010)‚حƒxƒ‹ƒMپ[‚جگ”ٹwژز‚إƒRƒ“ƒsƒ…پ[ƒ^‰بٹwژزپB
پ@پ@پi–َ’چ‚RپjBen WegbriteپFACM Programming Systems and Languages Paper Award in 1974.
پ@پ@پi–َ’چ‚SپjMichael KarrپFAffine relationships between variables of a program, Acta Informatica (1976)
پ@پ@پ@پ@پ@پ@پ@‚ئ‚¢‚¤ک_•¶‚ج’کژز‚ئ‚µ‚ؤ’ٹڈغ‰ًژك‚إ‚ح’m‚ç‚ê‚ؤ‚¢‚éپB
پ@پ@پi–َ’چ‚TپjSETL (SET Language)‚حڈWچ‡‚جگ”ٹw“I—ک_‚ةٹî‚أ‚¢‚½چ‚‹‰Œ¾ŒêپB1960”N‘مڈI‚è‚ة
پ@پ@پ@پ@پ@پ@پ@J. T. Schwartz‚ة‚و‚èٹJ”‚³‚ꂽپB
پ@پ@پi–َ’چ‚UپjJacob T. Schwartz (1930– 2009)‚حƒAƒپƒٹƒJ‚جگ”ٹwژزپAŒvژZ‹@‰بٹwژزپBƒvƒچƒOƒ‰ƒ~ƒ“ƒOŒ¾Œê
پ@پ@پ@پ@پ@پ@پ@SETL‚جگفŒvژزپB
پ@‚»‚ج–{ژ؟“I‚بٹT”O‚حپAƒvƒچƒOƒ‰ƒ€‚ج’ٹڈغ•]‰؟‚ًچs‚¤‚ئ‚«پAپu’ٹڈغپv’l‚حژہچغ‚ةƒvƒچƒOƒ‰ƒ€‚جژہچs‚إژg—p‚³‚ê‚éپu‹ï‘جپv’l‚ة‘م‚ي‚é•دگ”‚ةٹضŒW‚أ‚¯‚ç‚ê‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚ ‚éپBپi‘م“üپA•ھٹٍپAƒ‹پ[ƒvڈˆ—‚ب‚ا‚جپjŒ¾Œê‚جٹî–{‘€چى‚ح‰ًژك‚³‚êپA‚»‚جژپA’ٹڈغ‰ًژكپi‚ج–{ژ؟پj‚حگ„ˆع•آ•ïپiTransitive closureپjپi–َ’چ‚Pپj‚ج‹@چ\‚ة‚ ‚éپB—LŒہ‚إ‚ب‚¢ڈWچ‡‚ة‘®‚·‚é’ٹڈغ’l‚ًچl‚¦‚ؤ‚à‚و‚¢‚ھپAگ„ˆع•آ•ïƒAƒ‹ƒSƒٹƒYƒ€‚ج“ءگ«‚ح’ٹڈغ‰ًژك‚ھ—LŒہ‚جƒXƒeƒbƒv‚جŒم‚ةˆہ’è‚·‚é‚و‚¤‚ة‘I‚خ‚ê‚éپB‚±‚ê‚حƒRƒ“ƒpƒCƒ‹‚إٹ®‘S‚ة‰ًŒˆ‚إ‚«‚邱‚ئ‚ًˆس–،‚·‚éپBŒ¾Œê‚جٹî–{‘€چى‚جڈ‰“™“I‰ًژك‚ئ’ٹڈغ’l‚ج‘I‘ً‚حƒvƒچƒOƒ‰ƒ€‚©‚ç’ٹڈo‚µ‚½‚¢“ء’è‚ج“®“Iگ«ژ؟‚ةˆث‘¶‚·‚éپB’ٹڈغ’l‚ئٹî–{‘€چى‚ج‘I‘ً‚ھ‚±‚جک_•¶‚إ‹K’肵‚½ˆê”ت“I‚بƒtƒŒپ[ƒ€ƒڈپ[ƒN‚ً–‚½‚·‚ئ‚¢‚¤‚±‚ئ‚ًژ¦‚·‚±‚ئ‚ة‚و‚èپA’ٹڈغ•]‰؟ƒAƒ‹ƒSƒٹƒYƒ€‚جگ³‚µ‚³‚ئڈI—¹‚ھ•غڈط‚³‚ê‚éپB’Pڈƒ‰»‚ج–ع“I‚ج‚½‚ك‚ةپA‰نپX‚حPASCAL‚âLISپi–َ’چ‚Qپj‚ج‚و‚¤‚بچ‚‹‰Œ¾Œê‚جگ®گ”•دگ”‚ةŒ‹‚ر•t‚¯‚ؤ”حˆح‚جڈî•ٌ‚ًŒˆ’è‚·‚邱‚ئ‚ة‚و‚èپA‚±‚جژè–@‚ًگ}ژ¦‚·‚éپB
پ@پ@پi–َ’چ‚Pپjگ„ˆع•آ•ï‚ئ‚حپAڈWچ‡ X‚ة‚¨‚¯‚é“ٌچ€ٹضŒW R‚ة‘خ‚µ‚ؤپAR‚ًٹـ‚ق Xڈم‚جچإڈ¬‚جگ„ˆع
پ@پ@پ@پ@پ@پ@ٹضŒW‚ًˆس–،‚·‚éپB—ل‚¦‚خپAA={a,b,c,d}‚ج‚ئ‚«پAR‚ھAڈم‚جٹضŒW‚إ‚ ‚èپAR={(a,b),(b,c),(d,d)}
پ@پ@پ@پ@پ@پ@‚إ‚ ‚é‚ئ‚·‚é‚ئپAR‚حگ„ˆع—¥‚ھگ¬‚è—§‚½‚ب‚¢پB(a,b)پ¸R‚©‚آ(b,c)پ¸Rپث(a,c)پ¸R‚ھگ¬‚è—§‚½
پ@پ@پ@پ@پ@پ@‚ب‚¢‚©‚çپBگ„ˆع—¥‚ھگ¬‚è—§‚آ‚و‚¤‚ة—v‘f‚ً‰ء‚¦‚½چإڈ¬‚جٹضŒW‚ھگ„ˆع•آ•ïپB
پ@پ@پ@پ@پ@پ@‚±‚ê‚ًR'‚إ•\‚·‚ئR'={(a,b),(b,c),(a,c),(d,d)}
پ@پ@پi–َ’چ‚QپjLIsپFLISt Processor (ƒٹƒXƒgڈˆ—Œ¾Œê)‚ج‚±‚ئ‚©پB
‚QپD’ٹڈغ’l(Abstract Values)
پ@ƒvƒچƒOƒ‰ƒ€‚ج’ٹڈغ•]‰؟‚حپA‹ï‘ج“I‚ـ‚½‚حژہچs’l‚ج‘م‚ي‚è‚ة’ٹڈغ’l‚ًژg—p‚·‚éپAƒvƒچƒOƒ‰ƒ€‚جپuƒVƒ“ƒ{ƒٹƒbƒNپv‰ًژك‚إ‚ ‚éپB’ٹڈغ’l‚حپA‚¢‚‚آ‚©‚ج“®“IڈًŒڈ‚ً–‚½‚·‹ï‘ج’l‚جڈWچ‡‚â‚»‚ج‚و‚¤‚بڈWچ‡‚جگ«ژ؟‚ًژ¦‚·پBVc‚ً‹ï‘ج’l‚جڈWچ‡پAVa‚ً’ٹڈغ’l‚جڈWچ‡‚ئ‚·‚éپB
پ@‚±‚جک_•¶‚إ—^‚¦‚ç‚ê‚鑽‚‚ج—ل‚إ‚حپAVc‚حگ®گ”‚جڈWچ‡‚إ‚ ‚èپAVa‚حگ®گ”‚ج‹وٹش‚جڈWچ‡‚إ‚ ‚éپB‚à‚µپAVc=Z-پi-پ‡,+پ‡‚ًٹـ‚قگ®گ”‚جڈWچ‡پj‚ئ‚·‚é‚ئپAگ®گ”‚ج‹وٹش‚ح[a, b]پ@(a, bپ¸Z-, aپ…b)‚إ•\‚³‚ê‚éپB
پ@‹ï‘ج’l‚ئ’ٹڈغ’l‚جڈWچ‡ٹش‚ج‘خ‰‚حپu’ٹڈغ‰»ٹضگ”پvƒ؟‚ة‚و‚èٹm—§‚³‚ê‚éپF
پ@پ@پ@پ@پ@پ@پ@پ@پ@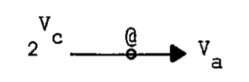
پ@پ@پiڈم‹L‚ج•\Œ»‚إپA2Vc‚حVc‚جƒxƒLڈWچ‡‚ًˆس–،‚·‚éپj
—لپF Sپ؛Z-‚ئ‚·‚é‚ئ‚«پAƒ؟(S)=[MIN(S), MAX(S)]
پ@پ@پ@—ل‚¦‚خپAƒ؟({-1, 5, 3})=[-1,5],ƒ؟({3, 4, 5,پEپEپE})=[3, +پ‡]
‚à‚¤ˆê‚آ‚جٹضگ”ƒء‚ح’ٹڈغ’l‚©‚ç‹ï‘ج’l‚ً—^‚¦‚éپF
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@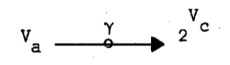
—لپFپ@ƒء([a, b])={ x | xپ¸Z-‚©‚آaپ…xپ…b }
پ@پ@پ@—ل‚¦‚خپAƒء([-1, 5])={-1, 0, 1, 2, 3, 4, 5}
ٹضگ”ƒ؟پAƒء‚ح‰؛‹L‚ً–‚½‚·‚و‚¤‚ة’è‹`‚³‚ê‚éپiƒKƒچƒA‘}“üپjپF
پ@پ@”Cˆس‚جsپ¸2Vc‚ة‘خ‚µ‚ؤپAsپ؛ƒء(ƒ؟(s))
پ@پ@”Cˆس‚جvپ¸Va‚ة‘خ‚µ‚ؤپAv=ƒ؟(ƒء(v))
پ@پiگ®گ”‚جڈWچ‡‚إ‚ ‚éپj‹ï‘ج’l‚جڈWچ‡‚جکaپ¾‚ة‘خ‰‚µ‚ؤپAپiگ®گ”‚ج‹وٹش‚جڈWچ‡‚إ‚ ‚éپj’ٹڈغ’l‚جکaپ¾پ`‚ھ’ٹڈغ•]‰؟‚ج‚½‚ك‚ة’è‹`‚³‚ê‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پF
پ@پ@پ@پ@پ@پ@پ@پ@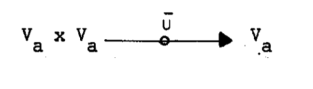
—لپFپ@[a1, b1]پ¾پ`[a2, b2] = [min(a1, a2), max(b1, b2)]
پy–َ‚إ‚ج•â‘«پzٹب’P‚ب—ل‚ً‰؛‹L‚ةژ¦‚·پG
پ@پ@‹ï‘ج’l‚جڈWچ‡‚ًA={-1, 5, 3}, B={0, 2, 6}‚ئ‚·‚é‚ئپAƒ؟(A)=[-1, 5],ƒ؟(B)=[0, 6]
پ@‚±‚ج‚ئ‚«پA‹ï‘ج’l‚جڈWچ‡A, B‚جکaAپ¾B={-1, 0, 2, 3, 5, 6}
پ@پ@پ@پ@پ@پ@پ@ ’ٹڈغ’lƒ؟(A),ƒ؟(B)‚جکaƒ؟(A)پ¾پ`ƒ؟(B)=[-1, 6]
پ@پ@‚ئ‚ب‚éپB‚±‚ج‚ئ‚«ƒ؟(Aپ¾B)=[-1, 6]‚ب‚ج‚إپA
پ@پ@پ@پ@پ@پ@پ@پ@پ@ƒ؟(Aپ¾B)=ƒ؟(A)پ¾پ`ƒ؟(B)
پ@پ@‚ھگ¬—§‚·‚éپB
پi‚»‚±‚إپj’ٹڈغٹضگ”ƒ؟‚حپi2Vc,پ¾)‚©‚çپiVa,پ¾پ`)‚ض‚جmorphismپi‚±‚±‚إ‚حپAکa‚جچ\‘¢‚ً•غ‘¶‚·‚éژت‘œپj‚إ‚ ‚é‚ئ‰¼’è‚·‚éپB‚·‚ب‚ي‚؟پA
پ@پ@پ@”Cˆس‚ج(s1, s2)پ؛Vcپ~Vc=Vc2‚ة‘خ‚µ‚ؤپAƒ؟پis1پ¾s2)=ƒ؟پis1پjپ¾پ`ƒ؟پis2)
‚±‚ê‚حپ¾پ`‚ھŒ‹چ‡“IپAŒًٹ·“IپA™p“™“Iپi–َ’چپjگ«ژ؟‚ًژ‚آ‚±‚ئ‚ًˆس–،‚µ‚ؤ‚¢‚éپB‚ـ‚½پA’ٹڈغ’l‚جnull‚ًپ ‚إ•\‚·‚ئپAƒ؟پiƒسپj=پ ‚إ‚ ‚éپiƒس‚ح‹ï‘ج’l‚جگ¢ٹE‚ج‹َڈWچ‡پjپB
پ@پ@پi–َ’چپj“ٌچ€‰‰ژZ "*"‚ً”ُ‚¦‚½ڈWچ‡ S‚ة‚آ‚¢‚ؤپAS‚جŒ³ s‚حs * s = s
پ@پ@پ@پ@پ@‚ً–‚½‚·‚ئ‚«پi"*"‚ةٹض‚µ‚ؤپj™p“™پiidempotentپj‚إ‚ ‚é‚ئ‚¢‚¤پB
پ@‹ï‘ج’l‚جڈWچ‡‚ج•ïٹـپ؛‚ةٹض‚µپA’ٹڈغ•]‰؟‚ح‰؛‹L‚إ’è‹`‚³‚ê‚é’ٹڈغ’l‚ج•ïٹـپ…پ`‚ًژg—p‚·‚éپi–َ’چپjپF
”Cˆس‚ج(v1, v2)پ؛Vaپ~Va=Va2‚ة‘خ‚µ‚ؤپA
پ@پ@پ@پ@پ@پ@v1پ…پ`v2‚ً v1پ¾پ`v2=v2
پ@پ@پ@پ@پ@پ@v1پƒپ`v2پ@‚ً {(v1پ…پ`v2)‚©‚آ(v1پ‚v2)}
‚ة‚و‚è’è‹`‚·‚éپB
پ@پ@پi–َ’چپj’ٹڈغ’l‚ج•ïٹـپ…پ`‚ھ’ٹڈغ’l‚جکaپ¾پ`‚ة‚و‚è’è‹`‚³‚ê‚ؤ‚¢‚邱‚ئ‚ة’چ–عپB
پ@‚±‚ج’è‹`‚ئپ¾پ`‚ة‚آ‚¢‚ؤ‚ج‰¼’è‚©‚çپAپ…پ`‚ح”¼ڈ‡ڈک‚إ‚ ‚邱‚ئ‚ًژ¦‚·‚±‚ئ‚ھ‚إ‚«پAپ ‚ح‘S‚ؤ‚ج’ٹڈغ’l‚ةٹـ‚ـ‚ê‚éپB
—لپFپ@[a1, b1]پ…پ` [a2, b2]پجپ@[a1, b1]پ¾پ`[a2, b2] = [min(a1, a2), max(b1, b2)] =[a2, b2]
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پج {(a2پ…a1)‚©‚آ(b2پ†b1)}
پ@پ…پ`‚ح”¼ڈ‡ڈک‚جگ«ژ؟پi”½ژث“IپAگ„ˆع“IپA‹t‘خڈج“Iپj‚ً–‚½‚·پBˆê•ûپAVa‚ح”Cˆس‚جv1, v2, v3پ¸Va‚ة‘خ‚µ‚ؤ‰؛‹L‚ھگ¬—§‚·‚é‚ج‚إVa=(Va,پ¾پ`)‚ح”¼‘©(semi-lattice)پi–َ’چپj‚إ‚ ‚éپBپG
پ@پ@پ@پ@پ@پ@(i) v1پ¾پ`v1=v1
پ@پ@پ@پ@پ@پ@پ@(ii) v1پ¾پ`v2= v2پ¾پ`v1
پ@پ@پ@پ@پ@پ@پ@(iii) v1پ¾پ`(v2پ¾پ`v3)= (v1پ¾پ`v2)پ¾پ`v3
پ@پ@پi–َ’چپj”¼‘©‚ج’è‹`‚¨‚و‚رگ«ژ؟‚حپuCousotڈ‰ٹْک_•¶‚ً“ا‚قپv‚ج‚QپD‚QپD‚Qچ€‚ًژQڈئپB
‚±‚ج‚ئ‚«پAڈ‡ڈکv1پ…پ`v2‚ھ v1پ¾پ`v2=v2‚ة‚و‚è’è‹`‚³‚ê‚ؤ‚¢‚é‚ج‚إپA’P’²‘‘ه—ٌ‚ة‘خ‚µ‚ؤٹ®”ُ‚ب”¼‘©‚ئ‚ب‚éپB
—لپF‹·‹`‚ج‘‰ءپi’چپj–³Œہچ½پFپ@پ , [1, 1], [1, 2], [1, 3],پEپEپEپ@‚حڈمŒہ[1,پ‡]‚ًژ‚آپBپ@
پ@پ@پi’چپj‹·‹`‚ج‘‰ء‚ئ‚ح“™چ†‚ًٹـ‚ـ‚ب‚¢گ^‚ج‘‰ء‚ج‚±‚ئپBچL‹`‚ج‘‰ء‚ح“™چ†‚ًٹـ‚قپB
پy–َ‚إ‚ج•â‘«پz’ٹڈغ’l‚جڈWچ‡Va‚ة‘خ‚µ‚ؤپAپu’ٹڈغ’l‚جکaپ¾پ`پv‚©‚çپu’ٹڈغ’l‚ج•ïٹـپ…پ`پv‚ھ’è‹`‚³‚êپA
پ@Va‚ھ”¼ڈ‡ڈکپ…پ`‚ج‰؛‚إٹ®”ُ‚ب”¼‘©‚ئ‚ب‚éپB
پ@پ¨‚±‚جٹ®”ُ‚ب”¼‘©‚حپuپ¾پ`پv‚ًƒxپ[ƒX‚ئ‚µ‚ؤچ\گ¬‚³‚ꂽ‚ج‚إپAپuٹ®”ُپ¾پ`پ|”¼‘©پv‚ئŒؤ‚شپB
پ@‚±‚جگك‚جچإŒم‚ةپAƒ‹پ[ƒv‚ج’ٹڈغ•]‰؟‚ة‚½‚ك‚ةپA—LŒہ‚جƒXƒeƒbƒv‚إ‹·‹`‚ة‘‰ء‚·‚é–³Œہچ½‚ج‹ةŒہ‚ًŒvژZ‚·‚é‚ئ‚¢‚¤–â‘è‚ًچl‚¦‚éپB‚±‚ج–ع“I‚ج‚½‚ك‚ةپAwidening‚ئŒؤ‚خ‚ê‚鉉ژZپقپ`‚ھ’è‹`‚³‚ê‚éپF
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@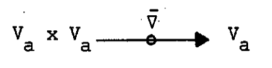
پقپ`‚حژں‚ج‚Q‚آ‚جڈًŒڈ‚ً–‚½‚·‚ئ‚«widening‰‰ژZژq‚ئ‚¢‚¤پF
پ| پقپ`‚حڈمٹE‰‰ژZژq‚إ‚ ‚éپG
پ@پ@‚·‚ب‚ي‚؟پA”Cˆس‚ج(v1, v2)پ؛Va2‚ة‘خ‚µ‚ؤپA(v1پ¾پ`v2)پ…پ`(v1پقپ`v2)
پ| ’P’²‘‘ه‚·‚éچ½v1, v2,پEپEپE, vn,پEپEپE ‚ة‘خ‚µ‚ؤپA
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@s0=v1, s1=s0پقپ`v1, s2=s1پقپ`v2,پEپEپE,sn=sn-1پقپ`vn, ,پEپEپE
پ@ ‚ح‹·‹`‚ج’P’²‘‘هچ½‚إ‚ح‚ب‚¢پi‚·‚ب‚ي‚؟پA—LŒہ‰ٌ‚إ‘‘ه‚ھژ~‚ـ‚éپjپB
—لپFwidening‰‰ژZژq‚ج—ل
پ@پ@پ@[a1, b1]پقپ` [a2, b2] = [ if a2<a1‚ب‚ç‚خپ|پ‡,‚»‚¤‚إ‚ب‚¢‚ب‚ç‚خa1,
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@if b2>b1‚ب‚ç‚خ+پ‡,‚»‚¤‚إ‚ب‚¢‚ب‚ç‚خb1"
پ@پ@پ@—ل‚¦‚خپA‹·‹`‚ج‘‰ء–³Œہچ½پFپ@پ , [1, 10], [1, 11], [0, 12], [-1, 13]پEپEپE‚ة‘خ‚µ‚ؤ
پ@پ@پ@ s1=پ پقپ`[1, 10]=[1, 10], s2=[1,10]پقپ`[1, 11]=[1, +پ‡], s3=[1, +پ‡]پقپ`[0, 12]=[-پ‡, +پ‡],
پ@پ@پ@پ@s4=[-پ‡, +پ‡]پقپ`[-1, 13]=[-پ‡, +پ‡]
پ@پ@پ@‚±‚جڈêچ‡پAsn‚ھ‹·‹`‚ج’P’²‘‰ء‚ئ‚ب‚é‚ج‚حn=4ˆب‰؛‚إ‚ ‚éپB
‚RپD’ٹڈغƒRƒ“ƒeƒLƒXƒg(Abstract contexts)
پ@ƒvƒچƒOƒ‰ƒ€‚ج’ٹڈغ•]‰؟‚ح‘S‚ؤ‚جƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒg‚إ‹كژ—‚ة‚و‚è’ٹڈغƒRƒ“ƒeƒLƒXƒg‚ًŒvژZ‚·‚éپBƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgrk(k=0, 1, 2,پEپEm)‚إ‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒg‚ح(i, v(rk))‚ئ‚¢‚¤ƒyƒA‚جڈWچ‡‚إ‚ ‚éپB‚±‚±‚إپA(i, v(rk))‚حژ¯•تژqiپi’چپj‚ھپAƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgrk‚إ’ٹڈغ’lv(rk)‚ًژ‚آ‚±‚ئ‚ً•\‚µپA’ٹڈغƒRƒ“ƒeƒLƒXƒg‚ج—v‘f‚حژ¯•تژqi‚إ‹و•ت‚³‚ê‚é‚à‚ج‚ئ‚·‚éپiپ¨‚±‚جˆس–،‚حپA—ل‚¦‚خ’ٹڈغƒRƒ“ƒeƒLƒXƒgC‚ج—v‘f‚ھ(i,v)‚ب‚ç‚خپA“¯‚¶ژ¯•تژqi‚ًژ‚آ—v‘f(i, v')‚ح•ت‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒgC'‚ج—v‘f‚إ‚ ‚é‚©پA‚ـ‚½‚حv=v'‚إ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پjپB
پ@پi’چپjژ¯•تژq(identifier)‚ئ‚حپA•دگ”پAژ葱‚«پAٹضگ”‚ج–¼‘O‚إ‚ ‚éپBژ¯•تژq‚إƒAƒNƒZƒX‚³‚ê‚é‘خڈغ‚ً
پ@پ@پ@پ@ƒIƒuƒWƒFƒNƒg‚ئ‚¢‚¤پB
پ@‚±‚ج‚ئ‚«پAƒvƒچƒOƒ‰ƒ€‚ج‘S‚ؤ‚جژہچغ‚جژہچs‚ة‚¨‚¢‚ؤپAi‚إƒAƒNƒZƒX‚³‚ê‚éƒIƒuƒWƒFƒNƒg‚ح‚»‚جƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒg‚إƒء(v)“à‚ة’l‚ھ‚ ‚éپB
پy–َ‚إ‚ج•â‘«پz
پu’ٹڈغƒRƒ“ƒeƒLƒXƒg‚ح(i, v)‚ئ‚¢‚¤ƒyƒA‚جڈWچ‡‚إ‚ ‚éپB‚±‚±‚إپA(i, v)‚حژ¯•تژqiپi’چپj‚ھپA‚ ‚éƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒg‚إ’ٹڈغ’lv‚ًژ‚آ‚±‚ئ‚ً•\‚·پBپv‚ئ‚حپA‰؛‹L‚جƒvƒچƒOƒ‰ƒ€‚إ‚ح‚ا‚¤‚ب‚é‚©‚ًژ¦‚·پG
پ@پ@پ@پ@پ@
‚±‚جƒvƒچƒOƒ‰ƒ€‚جژ¯•تژqپFxپ@پAƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgپFr0, r1,پEپEپE, r6
پ@پ@ƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgr1‚إ‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒgCr1=(x, [0, 0])
پ@پ@ƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgr2‚إ‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒgCr2,1=(x, [0, 1]), Cr2,2= (x, [0,2]),پEپEپE‚ب‚ا•،گ”‚ھ‚ ‚é
پ@پ@پiƒ‹پ[ƒv‰ٌگ”‚ةˆث‘¶‚·‚éپjپBپ¨‚±‚ج‚ئ‚«پA‹ï‘ج’l‚حƒء([0,1])={0,1},ƒء({0, 2])={0, 1, 2}“à‚ة‘¶چف‚·‚éپB
پ@پ@ƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒgr3‚ة‚آ‚¢‚ؤ‚à“¯—lپB
I‚ًژ¯•تژq‚جڈWچ‡‚ئ‚·‚é‚ئپA’ٹڈغƒRƒ“ƒeƒLƒXƒg‚جڈWچ‡C‚ح
پ@پ@پ@پ@پ@پ@پ@پ@Iپ~(Va-{پ })={ (i, v) | iپ¸I, vپ¸(Va-{پ }) }‚ج‘S‚ؤ‚ج•”•ھڈWچ‡پi=ƒxƒLڈWچ‡پj‚ةٹـ‚ـ‚ê‚éپB
’A‚µپAVaپF’ٹڈغ’l‚جڈWچ‡,پ پF’ٹڈغ’l‚جnullپB
‚ـ‚½پA—^‚¦‚ç‚ꂽ’ٹڈغƒRƒ“ƒeƒLƒXƒg‚جƒyƒA‚ح‚»‚ê‚ç‚جژ¯•تژq‚إ‹و•ت‚³‚ê‚éپF
‚·‚ب‚ي‚؟پA”Cˆس‚جi, jپ¸I‚ئ”Cˆس‚جv, uپ¸(Va-{پ })‚ة‘خ‚µ‚ؤپA
پ@(i, v), (j, u)پ¸C‚©‚آ(i, v)پ‚(j, u)‚ب‚ç‚خiپ‚j‚إ‚ ‚éپB
’ٹڈغƒRƒ“ƒeƒLƒXƒgCپ¸C‚ة‚¨‚¯‚éژ¯•تژqi‚ج’l‚ًC(i)‚ئ‚·‚éپB‚±‚ê‚ح‰؛‹L‚إ’è‹`‚إ‚«‚éپG
پ@C(i)={ if ( (i, v)پ¸C‚ئ‚ب‚évپ¸(Va-{پ })‚ھ‘¶چف‚·‚é ) then v elseپ }
پi—لپjپ@C={ (x, [1, 10]), (y, [-پ‡, 0]) }‚ئ‚·‚é‚ئپA
پ@پ@پ@پ@C(x)=[1, 10], C(z)=پ
“ء‚ةپAnull’ٹڈغƒRƒ“ƒeƒLƒXƒg‚ًƒس‚إ•\‚·پBڈم‹L‚ج’è‹`‚©‚çپA”Cˆس‚جiپ¸I‚ة‘خ‚µ‚ؤƒس(i)=پ ‚إ‚ ‚éپB
‚Q‚آ‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒgC, C'‚جکaCپ¾=C'‚حڈًŒڈ•¶(conditional statements)‚©‚çگ¶‚¶‚éƒRƒ“ƒeƒLƒXƒg‚ً•\Œ»‚·‚邽‚ك‚ةژg—p‚³‚êپA‚Q‚آ‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒg‚جwidening Cپق=C'‚حƒ‹پ[ƒv‚إژg—p‚³‚ê‚éپB‚±‚ê‚ç‚ح‰؛‹L‚إ’è‹`‚³‚ê‚éپG
C1پ¾=C2={(i, v) | iپ¸I‚©‚آvپ¸(Va-{پ })‚©‚آv=C1(i)پ¾پ`C2(i) }
C1پق=C2={(i, v) | iپ¸I‚©‚آvپ¸(Va-{پ })‚©‚آv=C1(i)پقپ`C2(i) }
‚±‚ê‚ç‚ة‚آ‚¢‚ؤ‚ح‰؛‹L‚جژ®‚ھگ¬‚è—§‚آپG
(C1پ¾=C2)(i)= C1(i)پ¾پ`C2(i)
(C1پق=C2)(i)= C1(i)پقپ`C2(i)
پi—ل‚PپjC1={ (x, [1, 10]), (y, [-پ‡, 0]) }, C2={ (x, [0, 5]), (z, [1, +پ‡]) }‚ئ‚·‚é‚ئپA
پ@پ@پ@C1(x)=[1,10], C2(x)=[0, 5], C1(y)=[-پ‡,0], C2(z)=[1, +پ‡]‚إ‚ ‚èپA
پ@پ@پ@C1(x)پ¾پ`C2(x)=[1, 10]پ¾پ`[0, 5]=[0, 10]‚ب‚ج‚إپA
پ@پ@پ@C1پ¾=C2= C2پ¾=C1={ (x, [0, 10]), (y, [-پ‡, 0]), (z, [1, +پ‡]) }
پ@پ@پ@‚ـ‚½پAC1(x)پقپ`C2(x)=[1,10]پقپ`[0, 5]=[ -پ‡, 10], C2(x)پقپ`C1(x)= [0,5]پقپ`[1, 10]=[0, +پ‡]
پ@پ@پ@C1(y)پقپ`C2(y)= [-پ‡,0]پقپ`پ =[-پ‡,0], C1(z)پقپ`C2(z)=پ پقپ`[1, +پ‡]= [1, +پ‡]‚ب‚ج‚إ
پ@پ@پ@C1پق=C2={ (x, [-پ‡, 10]), (y, [-پ‡, 0]), (z, [1, +پ‡]) }
پ@پ@پ@C2پق=C1={ (x, [0, +پ‡]), (y, [-پ‡, 0]), (z, [1, +پ‡]) }
پi—ل‚Qپj‘O‚ج•إ‚ج•â‘«‚جƒvƒچƒOƒ‰ƒ€—ل‚إ‚حپACr2,1=(x, [0, 1]), Cr2,2= (x, [0,2])‚ب‚ج‚إپA
پ@پ@پ@Cr2,1(x)پ¾=Cr2,2(x)= Cr2,2(x)پ¾=Cr2,1(x)=[0, 1]پ¾پ`[0, 2]=[0, 2]= Cr2,2(x)
ˆب‘O‚ئ“¯—l‚ةپAƒRƒ“ƒeƒLƒXƒg‚ج•ïٹـپ…=‚ً‰؛‹L‚إ’è‹`‚·‚éپG
پ@پ@پ@پ@پ@C1پ…=C2پجC1پ¾=C2=C2 , C1پƒ=C2پجC1پ…=C2‚©‚آC1پ‚C2
‚±‚ê‚ح‰؛‹L‚ئ“¯“™‚إ‚ ‚éپG
پ@پ@C1پ…=C2پج”Cˆس‚جiپ¸I‚ة‘خ‚µ‚ؤپAC1(i)پ…=C2(i)
پ@پi—لپj‘O‚ج•إ‚ج•â‘«‚جƒvƒچƒOƒ‰ƒ€—ل‚إ‚حپACr2,1(x)پ¾=Cr2,2(x)= Cr2,2(x)‚ب‚ج‚إپACr2,1پ…=Cr2,2
C‚ح”¼ڈ‡ڈکپ…=‚ج‰؛‚إٹ®”ُپ¾=”¼‘©‚إ‚ ‚éپB
‚³‚ç‚ةپA”Cˆس‚جC1, C2‚ة‘خ‚µ‚ؤپA
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@C1پ¾=C2پ…=C1پق=C2
‚إ‚ ‚èپA”Cˆس‚ج’ٹڈغƒRƒ“ƒeƒLƒXƒgC1, C2,پEپEپE, Cn,پEپEپE‚ة‘خ‚µ‚ؤwidening‰‰ژZژq‚ة‚و‚é—ٌ
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@S0=ƒس, S1=S0پق=C1,S2=S1پق=C2,پEپEپEپE,Sn=Sn-1پق=Cn,پEپEپEپE
‚ح—LŒہ‚إˆہ’è‚·‚é’P’²‘‰ء—ٌ‚ئ‚ب‚éپi–َ’چپjپB
پ@پi–َ’چپjwidening‰‰ژZژq‚جگ«ژ؟‚ة‚¨‚¢‚ؤ’P’²ٹضگ”f‚ئ‚µ‚ؤf(X)=X‚ًچl‚¦‚ê‚خ‚و‚¢پB
‚SپDƒvƒچƒOƒ‰ƒ€
پ@ƒvƒچƒOƒ‰ƒ€‚جچإڈ‰‚ج‹كژ—‚ئ‚µ‚ؤپA—LŒہ‚جƒtƒچپ[ƒ`ƒƒپ[ƒg‚ًژg—p‚·‚éپBƒtƒچپ[ƒ`ƒƒپ[ƒg‚حˆب‰؛‚جٹî–{“I‚بƒvƒچƒOƒ‰ƒ€ƒ†ƒjƒbƒg‚©‚ç‘g‚ف—§‚ؤ‚ç‚ê‚éپF
’Pˆê‚ج“üŒûƒmپ[ƒh پF![]()
ڈoŒûƒmپ[ƒhپ@پ@پ@پ@پ@پF![]()
‘م“üƒmپ[ƒhپ@پ@پ@پ@پ@پF![]()
ƒeƒXƒgƒmپ[ƒhپ@پ@پ@پ@پ@پF
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@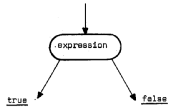
پi“ء’è‚جƒvƒچƒOƒ‰ƒ~ƒ“ƒOŒ¾Œê‚ج‘I‘ً‚ً”ً‚¯‚邽‚ك‚ةپA‘م“ü‚âƒeƒXƒg‚جژ®‚ج•]‰؟‚ح•›چى—p‚ھ‚ب‚¢‚ئ‚·‚éپj
’Pڈƒ‚بگعچ‡ƒmپ[ƒhپF
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@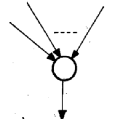
ƒ‹پ[ƒvگعچ‡ƒmپ[ƒhپF
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@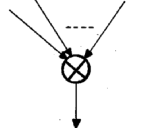
‚±‚±‚إ‚حگع‘±‚³‚ꂽƒtƒچپ[ƒ`ƒƒپ[ƒg‚ج‚ف‚ًچl‚¦پA—Bˆê‚ج“üŒûƒmپ[ƒh‚©‚½ƒtƒچپ[ƒ`ƒƒپ[ƒg‚ج‘S‚ؤ‚جƒmپ[ƒh‚ضڈ‚ب‚‚ئ‚àˆê‚آ‚جƒpƒX‚ھ‘¶چف‚·‚é‚ئ‚·‚éپB‚±‚ê‚ç‚جڈًŒڈ‚ئ‹¤‚ةپAƒtƒچپ[ƒ`ƒƒپ[ƒg‚ج‘S‚ؤ‚جƒTƒCƒNƒ‹‚حڈ‚ب‚‚ئ‚àˆê‚آ‚ج’Pڈƒ‚ـ‚½‚حƒ‹پ[ƒv‚جگعچ‡ƒmپ[ƒh‚ًٹـ‚ٌ‚إ‚¢‚é‚ئ‚·‚éپB‚³‚ç‚ةپAƒtƒچپ[ƒ`ƒƒپ[ƒg‚جڈ‰ٹْ‚جƒOƒ‰ƒt—ک_‰ًگح‚ھچs‚ي‚êپA‘S‚ؤ‚جƒTƒCƒNƒ‹‚حڈ‚ب‚‚ئ‚àˆê‚آ‚جƒ‹پ[ƒvگعچ‡ƒmپ[ƒh‚ًٹـ‚فپAƒ‹پ[ƒvگعچ‡ƒmپ[ƒh‚حچإڈ¬‚ة‚ب‚ء‚ؤ‚¢‚é‚ئ‚·‚éپB
—لپF
پ@پ@پ@پ@پ@پ@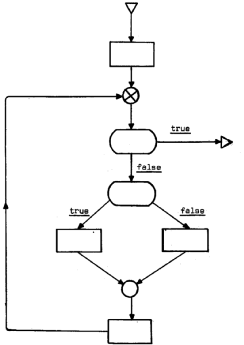
‚TپDٹî–{ƒvƒچƒOƒ‰ƒ€ƒ†ƒjƒbƒg‚جڈ‰“™“I’ٹڈغ‰ًژك
پ@’ٹڈغ•]‰؟ƒAƒ‹ƒSƒٹƒYƒ€‚ج“K—p‚ج‚½‚ك‚ةپAٹî–{ƒvƒچƒOƒ‰ƒ€ƒ†ƒjƒbƒg‚ج•]‰؟‚ج’è‹`‚ً’ٌ‹ں‚µ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB”Cˆس‚ج‘م“ü‚ـ‚½‚حƒeƒXƒgƒvƒچƒOƒ‰ƒ€ƒ†ƒjƒbƒgn‚ئ“ü—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgC‚ة‘خ‚µپAڈo—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgTپ|(n, C)‚ًˆبچ~‚إ’è‹`‚·‚éپBTپ|‚حƒvƒچƒOƒ‰ƒ€ƒ†ƒjƒbƒgn‚جژہچs‚جگ³‚µ‚¢پu’ٹڈغپv‚إ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB
‚TپD‚Pپ@‘م“üƒmپ[ƒh‚جڈ‰“™“I’ٹڈغ‰ًژكTپ|(n, C)
پ@Na‚ً‘م“üƒmپ[ƒh‚جڈWچ‡‚ئ‚·‚éپB”Cˆس‚جnپ¸Na‚ة‘خ‚µ‚ؤپA‘م“üƒmپ[ƒhn‚ح‰؛‹L‚جŒ`ژ®‚إ•\Œ»‚³‚ê‚éپF
پ@پ@پ@پ@پ@![]()
‚±‚±‚إپAv, v1,پEپEپE,vm‚حژ¯•تژqپi•دگ”پj‚إ‚ ‚èپAf(v1,پEپEپE,vm)‚ح•دگ”v1,پEپEپE,vm‚ةŒ¾Œêˆث‘¶‚·‚éژ®‚إ‚ ‚éپB
‚±‚ج‚ئ‚«پA”Cˆس‚ج“ü—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgCپ¸C‚ئ”Cˆس‚جiپ¸I‚ة‘خ‚µ‚ؤپATپ|(n, C)‚ً
پ@پ@پE iپ‚v‚ب‚ç‚خپATپ|(n, C)(i)=C(i)پ@پEپEپE…@
پ@پ@پE i=v‚ب‚ç‚خپATپ|(n, C)(v)=ƒ؟({f(ƒت1,پEپEپE,ƒتm) |ƒت1پ¸ƒء(C(v1)),پEپEپE,ƒتmپ¸ƒء(C(vm))})پEپEپE…A
‚ة‚و‚è’è‹`‚·‚éپBچإڈ‰‚جڈًŒڈژ®…@‚حf(v1,پEپEپE,vm)‚ة‚و‚év‚ج’l‚ھTپ|(n, C)(i)‚ة‰e‹؟‚ً—^‚¦‚ب‚¢‚±‚ئ‚ًژ¦‚µپA
“ٌ”ش–ع‚جڈًŒڈژ®…A‚حپA“ü—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgC‚ة‚و‚év1,پEپEپE,vm‚ج’ٹڈغ’lC(v1),پEپEپE,C(vm)‚ً‹ï‘ج‰»ٹضگ”ƒء‚إ–ك‚µ‚½ƒء(C(v1)),پEپEپE,ƒء(C(vm))‚ة‘®‚·‚é‹ï‘ج’l‚ًƒت1,پEپEپE,ƒتm‚ئ‚·‚é‚ئ‚«پAژ®f(ƒت1,پEپEپE,ƒتm)‚ج’l‚ج’ٹڈغ‰»ƒ؟({f(ƒت1,پEپEپE,ƒتm) |ƒت1پ¸ƒء(C(v1)),پEپEپE,ƒتmپ¸ƒء(C(vm))})‚ھڈo—ح’ٹڈغƒRƒ“ƒeƒLƒXƒg‚جv‚إ‚ج’l
Tپ|(n, C)(v)‚إ‚ ‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پi—ل‚Pپj‘O‚ج•إ‚ج•â‘«‚جƒvƒچƒOƒ‰ƒ€—ل‚إ‚حپA‘م“üƒmپ[ƒh‚جژ®‚ح
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@x:=f(x)=x+1
پ@پ@پ@‚إ‚ ‚éپB“ü—حƒRƒ“ƒeƒLƒXƒg‚ًCr3,1=(x, [0, 1])‚ئ‚·‚é‚ئپA
پ@پ@پ@Tپ|(n, C)(x)=ƒ؟( {f(ƒت) |ƒتپ¸ƒء(C(x)) } ]=ƒ؟[ {f(ƒت) |ƒتپ¸ƒء([0, 1]) } )
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@=ƒ؟( {f(ƒت) |ƒت=0, 1} )=ƒ؟( {x:=ƒت+1 |ƒت=0, 1} )=ƒ؟({x=1, 2})=[1, 2]
پi—ل‚Qپj‰؛‹L‚جگ}‚حپA
پ@پ@پ@پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC=ƒسپi‹َڈWچ‡پjپA‘م“üƒmپ[ƒh‚جژ®پFپ@x:=10
پ@پ@پ@پ@‚ئ‚·‚é‚ئ‚«پATپ|(n, C)={ (x, [10, 10]) }‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@پ@پ@پ@پ@پ@پ@پ@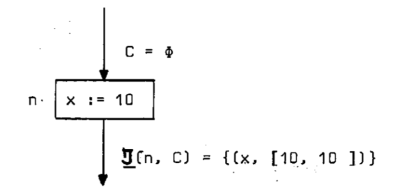
پ@پ@پ@‰ًگàپFTپ|(n, C)(x)=ƒ؟( {f(ƒت) |ƒتپ¸ƒء(C(x)) } )=ƒ؟( {x:=10 |ƒتپ¸ƒء(undefined) } )
پ@پ@پ@پ@پ@پ@پ@=ƒ؟(x:=10)=[10, 10]پ@پ@‚µ‚½‚ھ‚ء‚ؤپATپ|(n, C)={ (x, [10, 10]) }
پi—ل‚Rپj‰؛‚جگ}‚حپA
پ@پ@پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC={ (x, [1, 10] ), (y, [-2, 3] ) }پA‘م“üƒmپ[ƒh‚جژ®پFپ@x:=x+y+1
پ@پ@پ@پ@‚ئ‚·‚é‚ئ‚«پATپ|(n, C)={ (x, [0, 14] ), (y, [-2, 3] ) }‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@پ@پ@پ@پ@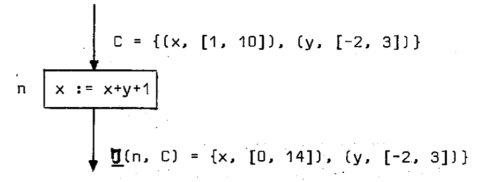
پ@پ@پ@پ@پ@‰ًگàپFTپ|(n, C)(x)=ƒ؟({f(ƒت1,ƒت2) |ƒت1پ¸ƒء(C(x)), ƒت2پ¸ƒء(C(y)) } )
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@=ƒ؟({x:=ƒت1+ƒت2+1 |ƒت1پ¸ƒء( [1, 10]), ƒت2پ¸ƒء( [-2, 3]) } )
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@=ƒ؟({x:=ƒت1+ƒت2+1 |ƒت1=1,2,پEپEپE,10ƒت2=-2,-1,0,1,2,3 } )
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@=ƒ؟( x:=0,1,2,3,4,5,6,7,8,9,10,11,12,13,14 )=[0, 14]پ@پEپEپE(1)
پ@پ@پ@پ@پ@پ@پ@پ@پ@yپ‚x‚ب‚ج‚إپATپ|(n, C)(y)=C(y)=[-2, 3]پEپEپE(2)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@(1), (2)‚و‚èTپ|(n, C)={ (x, [0, 14] ), (y, [-2, 3] ) }‚ھ“¾‚ç‚ê‚éپB
پi—ل‚Sپj‰؛‚جگ}‚حپA
پ@پ@پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC={ (x, [1, 10] ), (z, [-1, 1] ) }پA‘م“üƒmپ[ƒh‚جژ®پFپ@x:=x+y
پ@پ@پ@پ@‚ئ‚·‚é‚ئ‚«پATپ|(n, C)={ (z, [-1, 1] ) }‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@پ@پ@پ@پ@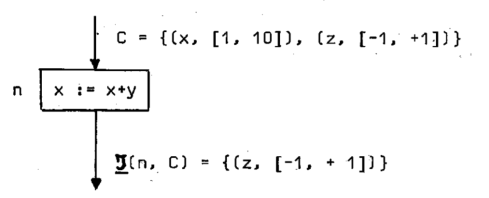
پ@پ@‰ًگàپFC(y)=پ ‚ب‚ج‚إx:=x+y‚ح–¢’è‹`‚ئ‚ب‚éپB‚µ‚½‚ھ‚ء‚ؤپATپ|(n, C)(x)=پ
پ@پ@پ@پ@پ@پ@zپ‚x‚ب‚ج‚إپATپ|(n, C)(z)=C(z)=[-1, 1]
‚TپD‚Qپ@ƒeƒXƒgƒmپ[ƒh‚جڈ‰“™“I’ٹڈغ‰ًژكTپ|(n, C)
پ@“ü—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgC‚حƒeƒXƒgƒmپ[ƒh‚ة‚و‚èگ^‚ئ‹U‚ةٹضŒW‚·‚é‚Q‚آ‚جڈo—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgCT‚ئCF‚ًگ¶‚¶‚éپB
NT‚ًƒeƒXƒgƒmپ[ƒh‚جڈWچ‡‚ئ‚·‚éپB”Cˆس‚جnپ¸NT‚ة‘خ‚µ‚ؤپAn‚ح‰؛‹L‚ج—lژ®‚ئ‚·‚éپG
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@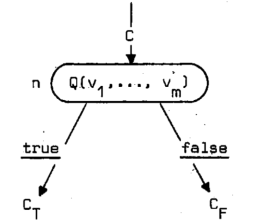
‚±‚±‚إپAQ(v1,پEپEپE,vm)‚ح•دگ”v1,پEپEپE,vm‚ةˆث‘¶‚·‚éƒuپ[ƒ‹ژ®پi–َ’چپj‚إ‚ ‚éپB
پ@پi–َ’چپjƒuپ[ƒ‹ژ®‚حپATRUE‚ـ‚½‚حFALSE‚جک_—•¶پBƒuپ[ƒ‹ژ®‚إ‚حپA”نٹr‚·‚é—¼•û‚جژ®‚جٹî–{ƒfپ[ƒ^
پ@پ@پ@پ@پ@Œ^‚ھ“¯‚¶‚إ‚ ‚ê‚خپA‚·‚ׂؤ‚جŒ^‚جƒfپ[ƒ^‚ً”نٹr‚إ‚«‚éپBƒfپ[ƒ^‚ًƒeƒXƒg‚µپA‘¼‚جƒfپ[ƒ^‚ئ“™‚µ‚¢پA
پ@پ@پ@پ@پ@‚و‚è‘ه‚«‚¢پA‚ـ‚½‚ح‚و‚èڈ¬‚³‚¢‚©‚ً’²‚ׂ邱‚ئ‚ھ‚إ‚«‚éپB
‚±‚ج‚ئ‚«Tپ|(n, C)=(CT, CF)‚ً‰؛‹L‚إ’è‹`‚·‚éپF
”Cˆس‚جiپ¸I‚ة‘خ‚µ‚ؤپA“ü—ح’ٹڈغƒRƒ“ƒeƒLƒXƒgC‚ة‚و‚év1,پEپEپE,vm‚ج’ٹڈغ’lC(v1),پEپEپE,C(vm)‚ً‹ï‘ج‰»ٹضگ”ƒء‚إ–ك‚µ‚½ƒء(C(v1)),پEپEپE,ƒء(C(vm))‚ة‘®‚·‚é‹ï‘ج’l‚ًƒت1,پEپEپE,ƒتm‚ئ‚·‚é‚ئ‚«پA
CT(i)=ƒ؟( {ƒر|ƒرپ¸ƒء(C(i)) }‚©‚آ{ Q(ƒت1,پEپEپE,ƒتm)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء(C(v1)),پEپEپE,ƒتmپ¸ƒء(C(vm)) }
CF(i)=ƒ؟( {ƒر|ƒرپ¸ƒء(C(i)) }‚©‚آ{ Q(ƒت1,پEپEپE,ƒتm)‚ھ‹U‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء(C(v1)),پEپEپE,ƒتmپ¸ƒء(C(vm)) }
پi—ل‚Pپj‰؛‚جگ}‚حپA
پ@پ@پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC={ (x, [-پ‡, +پ‡] ) }پAƒeƒXƒgƒmپ[ƒh‚جژ®پFپ@xپ†0
پ@پ@پ@پ@‚ئ‚·‚é‚ئ‚«پACT={ (x, [0, +پ‡] )}پACF={ (x, [-پ‡, -1] ) }‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@پ@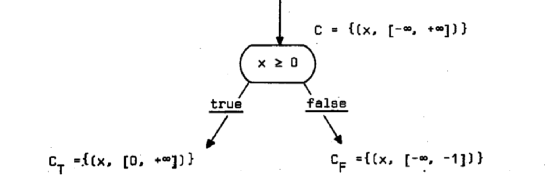
پ@پ@پ@‰ًگàپFƒeƒXƒgƒmپ[ƒh‚ح’ٹڈغ’lxپ†0‚ب‚ج‚إQ(x)= if xپ†0 then true, else false‚ئ‚ب‚éپB‚µ‚½‚ھ‚ء‚ؤپA
پ@پ@پ@CT(x)=ƒ؟( {ƒر|ƒرپ¸ƒء(C(x)) }‚©‚آ{ Q(ƒت)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒتپ¸ƒء(C(x)) }
پ@پ@پ@پ@پ@پ@پ@=ƒ؟( {ƒر|ƒرپ¸ƒء([-پ‡, +پ‡]) }‚©‚آ{ Q(ƒت)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒتپ¸ƒء([-پ‡, +پ‡]) } )
پ@پ@پ@پ@پ@پ@پ@=ƒ؟({ƒر=-پ‡,پEپEپE-2,-1,0,1,2,پEپEپE+پ‡ }‚©‚آ{ƒت=0,1,2,پEپEپE+پ‡ } )
پ@پ@پ@پ@پ@پ@پ@=[0, +پ‡]
پ@پ@پ@CF(x)=ƒ؟( {ƒر|ƒرپ¸ƒء([-پ‡, +پ‡]) }‚©‚آ{ Q(ƒت)‚ھ‹U‚ئ‚ب‚é‚و‚¤‚بƒتپ¸ƒء([-پ‡, +پ‡]) } )
پ@پ@پ@پ@پ@پ@=ƒ؟({ƒر=-پ‡,پEپEپE-2,-1,0,1,2,پEپEپE+پ‡ }‚©‚آ{ƒت=-پ‡,پEپEپE-2,-1 } )
پ@پ@پ@پ@پ@پ@= [-پ‡, -1]
پi—ل‚Qپj‰؛‚جگ}‚ح
پ@پ@پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC={ (x, [-پ‡, +پ‡] ), (y, [1,10]) }پAƒeƒXƒgƒmپ[ƒh‚جژ®پFپ@xپ†y
پ@پ@پ@پ@‚ئ‚·‚é‚ئ‚«پACT={ (x, [1, +پ‡] ), (y, [1,10]) }پACF={ (x, [-پ‡, 9] ), (y, [1, 10]) }‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@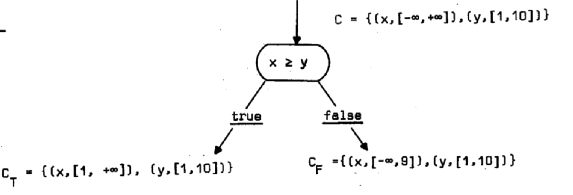
پ@پ@پ@‰ًگàپFƒeƒXƒgƒmپ[ƒh‚ح’ٹڈغ’lxپ†y‚ب‚ج‚إQ(x, y)= if xپ†y then true, else false‚ئ‚ب‚éپB
پ@پ@پ@CT(x)=ƒ؟( {ƒر|ƒرپ¸ƒء(C(x)) }‚©‚آ{ Q(ƒت1,ƒت2)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء(C(x)),ƒت2پ¸ƒء(C(y)) }
پ@پ@پ@پ@پ@پ@پ@=ƒ؟( {ƒر|ƒرپ¸ƒء([-پ‡, +پ‡]) }‚©‚آ{ Q(ƒت1,ƒت2)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء([-پ‡, +پ‡]),
پ@پ@پ@پ@پ@پ@پ@پ@ƒت2پ¸ƒء([1, 10]) }=ƒ؟({ƒر=-پ‡,پEپEپE-2,-1,0,1,2,پEپEپE+پ‡ }‚©‚آ{ƒت1=10, 11, ,پEپEپE+پ‡ })
پ@پ@پ@پ@پ@پ@پ@=[-پ‡, +پ‡]پ؟[10, +پ‡]= [10, +پ‡]
پ@پ@پ@CT(y)=ƒ؟( {ƒر|ƒرپ¸ƒء(C(y)) }‚©‚آ{ Q(ƒت1,ƒت2)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء(C(x)),ƒت2پ¸ƒء(C(y)) }
پ@پ@پ@پ@پ@پ@پ@پ@==ƒ؟( {ƒر|ƒرپ¸ƒء([1,10]) }‚©‚آ{ Q(ƒت1,ƒت2)‚ھگ^‚ئ‚ب‚é‚و‚¤‚بƒت1پ¸ƒء([-پ‡, +پ‡]),
پ@پ@پ@پ@پ@پ@پ@پ@ƒت2پ¸ƒء([1, 10]) }=ƒ؟({ƒر=1,2,پEپEپE,10}‚©‚آ{ƒت2=1,2,پEپEپE,10 })=[1, 10]پ؟[1,10]=[1,10]
‚TپD‚Rپ@Œ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒg
پ@Œ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒg‚ًŒvژZ‚·‚邽‚ك‚ةپAŒ‹چ‡ƒmپ[ƒh‚ج“ü—حƒRƒ“ƒeƒLƒXƒg‚ًچإڈ‰‚ةŒvژZ‚µ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB’Pڈƒ‚بŒ‹چ‡ƒmپ[ƒhn‚ً‰؛‹L‚ةژ¦‚·پF
پ@پ@پ@پ@پ@پ@پ@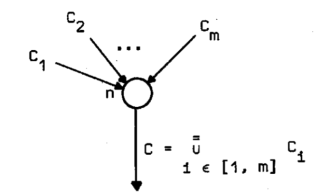
‚±‚±‚إپAC1, C2,پEپEپE, Cm‚حŒ‹چ‡ƒmپ[ƒhn‚ج“ü—حƒRƒ“ƒeƒLƒXƒg
C=پ¾=Ci, iپ¸[1, m]‚حŒ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒg
پi—لپj‰؛‚جگ}‚حپA
پ@پ@“ü—حƒRƒ“ƒeƒLƒXƒgپFC1={ (x, [1, 1] ) }, C2={ (x, [2, 2]) }‚ئ‚·‚é‚ئ‚«پA
پ@پ@Œ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒgپFC= C1پ¾=C2={ (x, [1, 1]پ¾پ`[2, 2] ) }={ (x, [1, 2] ) }
پ@پ@‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@پ@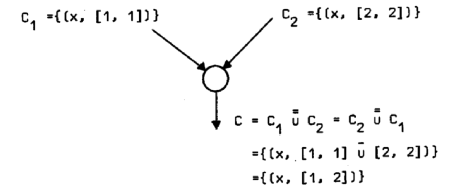
‚TپD‚Sپ@ƒ‹پ[ƒvŒ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒg
پ@‚±‚جگك‚حک_•¶‚ج–َ‚إ‚ح‚ب‚ٹب’P‚ب—ل‚إ‚ج‰ًگà‚ًڈq‚ׂéپB—ل‚¦‚خپA‰؛‚ج‚و‚¤‚ب—ل‚ًچl‚¦‚ؤ‚ف‚éپB
‚±‚جڈêچ‡پAƒ‹پ[ƒv‚ة‚حڈم‚©‚ç‚ئ‰،‚©‚ç‚ئ‚¢‚¤‚Q‚آ‚ج•ûŒü‚©‚ç‚ج“ü—ح‚ھ‚ ‚èپAڈo—ح‚ح‰؛•ûŒü‚P‚آ‚إ‚ ‚éپG
پ@پ@پ@پ@پ@
ƒ‹پ[ƒv‚جچإڈ‰‚ج“ü—حƒRƒ“ƒeƒLƒXƒg‚حڈم‚©‚ç‚حInputC1={ (i, [1, 1] ) }‚إ‚ ‚éپB‰،‚©‚ç‚جڈ‰‰ٌ‚حژہچغ‚ة‚ح‚ب‚¢‚ھ‹َڈWچ‡‚ج“ü—حInputC2,1=ƒس‚ھ‚ ‚é‚ئچl‚¦‚éپB‚µ‚½‚ھ‚ء‚ؤپA‚±‚جƒ‹پ[ƒv‚جڈ‰‰ٌ(j=1)‚جڈo—ح‚حOutputC1= InputC1پ¾=InputC2,1={ (i, [1, 1] ) }پ¾=ƒس={ (i, [1, 1] ) }‚إ‚ ‚éپG
پ@پ@پ@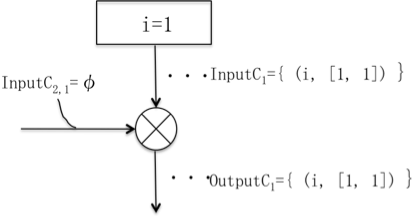
‚±‚جƒ‹پ[ƒv‚ج‚Q‰ٌ–ع‚ج“ü—حƒRƒ“ƒeƒLƒXƒg‚حInputC1={ (i, [1, 1] ) }‚ئInputC2,2={ (i, [2, 2] ) }‚إ‚ ‚èپA
‚Q‰ٌ–ع‚جڈo—حƒRƒ“ƒeƒLƒXƒg‚حOutputC2=InputC1پ¾=InputC2.2={ (i, [1, 1] ) }پ¾={ (i, [2, 2] ) }={ (i, [1, 2]) }
‚ئ‚ب‚éپG
پ@
‚R‰ٌ–ع‚ًچl‚¦‚é‚ئپA‚±‚جƒ‹پ[ƒv‚ج‚R‰ٌ–ع‚ج“ü—حƒRƒ“ƒeƒLƒXƒg‚حInputC1={ (i, [1, 1] ) }‚ئInputC2,3={ (i, [3, 3] ) }‚إ‚ ‚èپA‚R‰ٌ–ع‚جڈo—حƒRƒ“ƒeƒLƒXƒg‚حOutputC3=InputC1پ¾=InputC2.3={ (i, [1, 1] ) }پ¾={ (i, [3, 3] ) }=
{ (i, [1, 3]) }‚ئ‚ب‚éپG
پ@پ@پ@
“¯—l‚ة‚µ‚ؤپAj‰ٌ–ع‚ج“ü—حƒRƒ“ƒeƒLƒXƒg‚حInputC1={ (i, [1, 1] ) }‚ئInputC2,j={ (i, [j, j] ) }‚إ‚ ‚èپAj‰ٌ–ع‚جڈo—حƒRƒ“ƒeƒLƒXƒg‚حOutputCj=InputC1پ¾=InputC2.j={ (i, [1, 1] ) }پ¾={ (i, [j, j] ) }={ (1, [1, j ] ) }‚ئ‚ب‚éپG
پ@پ@
پ@‚±‚ê‚ً—LŒہ‰ٌ‚إڈWŒ‹‚³‚¹‚邽‚ك‚ةƒ‹پ[ƒvŒ‹چ‡ƒmپ[ƒh‚جڈo—حƒRƒ“ƒeƒLƒXƒg‚©‚çچى‚ç‚ê‚éwidening‚ھژg—p‚³‚ê‚éپF‚·‚ب‚ي‚؟پA‰؛‚جگ}‚ج‚و‚¤‚ةOutputC1, OutputC2, OutputC3,پEپE‚ئ‚¢‚¤’P’²‘‘ه‚·‚é–³ŒہŒn—ٌ‚ج‘م‚ي‚è‚ة‚»‚ê‚ç‚جwidening‚©‚çS1, S2,پEپE‚ئ‚¢‚¤—LŒہ‰ٌ‚إˆہ’è‚·‚éŒn—ٌ‚ھچى‚ç‚ê‚éپB‚±‚ج—ل‚جڈêچ‡پA‚Q‰ٌ–ع‚إwidening‚ة‚و‚éڈo—حƒRƒ“ƒeƒLƒXƒg‚ح{ (i, [1,پ‡] ) }‚ئ‚¢‚¤’l‚ةˆہ’è‚·‚éپB
پ@پ@پ@پ@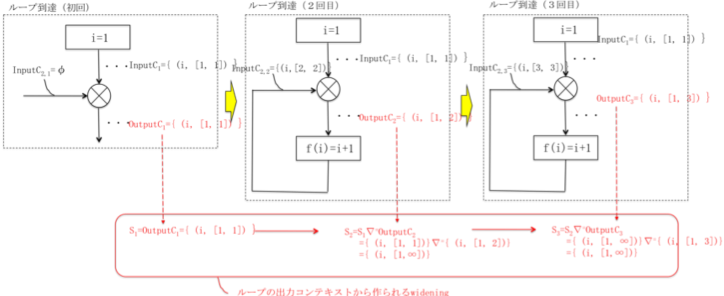
‚UپD’ٹڈغ‰ًژكٹي(Abstract Interpretor)
پ@’ٹڈغ‰ًژكٹي‚ح‘S‚ؤ‚جŒتپi=ƒvƒچƒOƒ‰ƒ€ƒ|ƒCƒ“ƒg)‚إ‹َڈWچ‡‚جƒRƒ“ƒeƒLƒXƒgƒس‚©‚çƒXƒ^پ[ƒg‚·‚éپB‘و‚Tگك‚إ‰نپX‚حپAپi‘م“üƒmپ[ƒhپAƒeƒXƒgƒmپ[ƒhپAŒ‹چ‡ƒmپ[ƒhپAƒ‹پ[ƒvŒ‹چ‡ƒmپ[ƒh‚ب‚ا‚جپjˆظ‚ب‚éƒ^ƒCƒv‚جƒmپ[ƒh‚ة‘خ‚µ‚ؤپA‚»‚ج“ü—حŒت‚جƒRƒ“ƒeƒLƒXƒg‚©‚çƒmپ[ƒh‚جڈo—حŒت‚جƒRƒ“ƒeƒLƒXƒg‚ً‹K’è‚·‚é•دٹ·‚ً‹Lڈq‚µ‚ؤ‚«‚½پB‚»‚جƒAƒ‹ƒSƒٹƒYƒ€‚ح‘S‚ؤ‚جƒRƒ“ƒeƒLƒXƒg‚ھˆہ’è‚·‚é‚ـ‚إ‚±‚ê‚ç‚ج•دٹ·‚ج“K—p‚ًچs‚¤‚±‚ئ‚إ‚ ‚éپB‚·‚ب‚ي‚؟پA”Cˆس‚جƒmپ[ƒh‚إ‚»‚ج•دٹ·‚ً‚¢‚‚ç“K—p‚µ‚ؤ‚àڈo—حŒت‚جƒRƒ“ƒeƒLƒXƒg‚ھ•د‰»‚µ‚ب‚‚ب‚éڈَ‘ش‚ًچى‚邱‚ئ‚إ‚ ‚éپB
پ@ˆê”ت“I‚ب’ٹڈغ‰ًژكٹي‚ح‰؛‹L‚جژèڈ‡‚إچى‚ç‚ê‚éپG
پ@پ@پ@پ@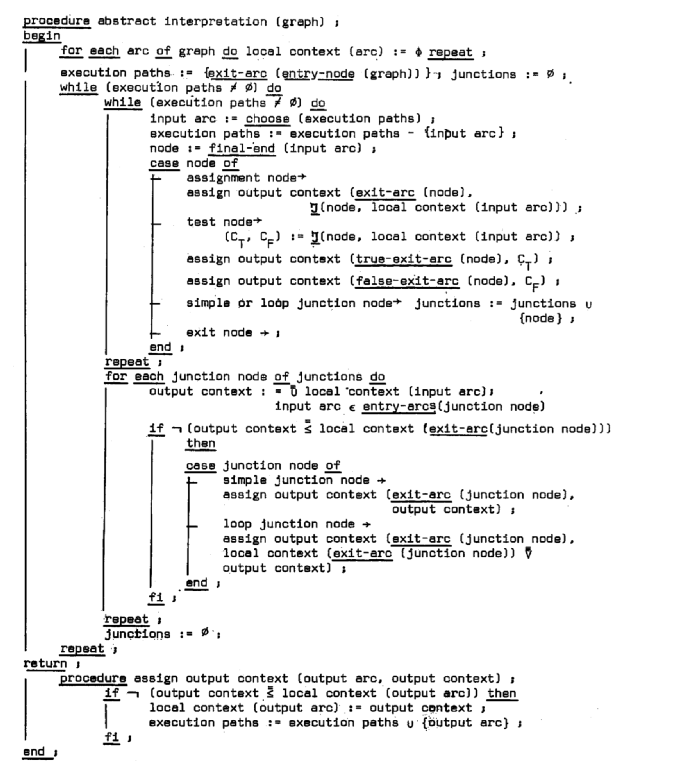
—لپF
پ@پ@پ@پ@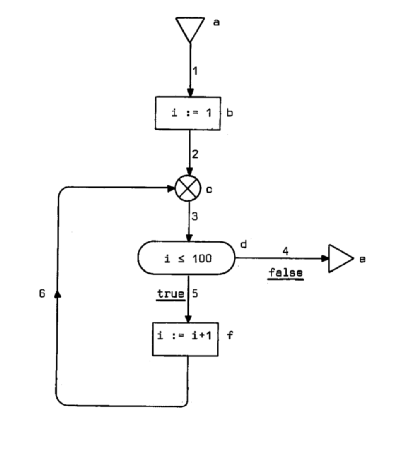
‰؛‹L‚ج•\‚ح–{ک_•¶‚إژ¦‚µ‚½’ٹڈغ‰ًژك‚ة‚و‚éڈم‹L‚جƒvƒچƒOƒ‰ƒ€ƒOƒ‰ƒt‚ج‰ًگح‚ًژ¦‚µ‚ؤ‚¢‚éپG
پ@پ@پ@پ@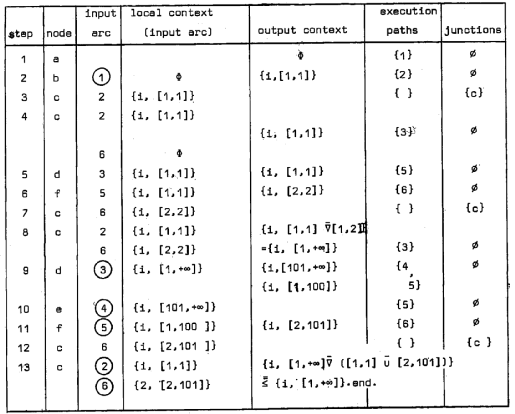
ƒtƒچپ[ƒ`ƒƒپ[ƒg‚ًژہچs‚µ‚½‚ئ‚«‚جٹeŒت‚جچإڈIƒRƒ“ƒeƒLƒXƒg‚حinput arc‚ج”شچ†‚ةٹغˆَ‚إژ¦‚³‚ê‚ؤ‚¢‚éپB