MTF概要(CloudyNightのEquipmentDiscussionsの2011年2月のスレッド;
How to understand an MTF chart...の内容紹介)
(*)http://www.cloudynights.com/ubbthreads/showflat.php/Cat/0/Number/4415334/page/0/
view/collapsed/sb/5/o/all/fpart/all/vc/1
2014年3月作成:舟越 和己
Cloudy Nightsの上記のMTFについての説明は非常に良い内容です。
以下ではこれを図解にして簡単に紹介します。
1.準備(予備知識)
1.1 解像度テストチャート
・下の図のような各々0.5mmの幅の白と黒のラインが交互に繰り返している解像力テストチャート
を考えます。
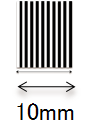
・このチャートは、1mmの幅に「白黒ラインの組」が1組あり、全体で10組の「白黒ラインの組」から
構成されています。
・また、このテストチャートは、完全な白と完全な黒、すなわち白の強度=10, 黒の強度=0とします。
このとき、
Modulation=(10-0)/(10+0)=1.0
なので、そのコントラストは100%です。
・一般に、1mmあたりの白黒ラインの組の数をlp/mm(Line pairs per millimeter)と言います。
→下の図①では、1mmあたり1組なので1lp/mmです。
また、下の図②のように、1mmあたり60組の白黒ラインの組があれば、これは60lp/mmです。
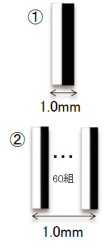
・白黒ラインの1組が正弦波の1波長に該当します。(このため「白黒ラインの1組」を1サイクルと
呼ぶこともあります)
→上の図の①は1波長=1mm, ②は1波長=1/60mm
従って、
「1ミリあたりの白黒ラインの組の数=1/波長
=空間周波数(Spatial Frequency)」が成立する(重要!)
→右図の①の空間周波数=1lp/mm, ②の空間周波数=60lp/mm
※空間周波数は角度で考える場合もある。→後で説明有。
1.2 等倍の望遠鏡
・下の図のように望遠鏡に10mmの視野絞りを持つアイピースを入れて、その望遠鏡で解像力
テストチャートを見たときに10組ラインになるようにチャートを望遠鏡の前方に置く。

・これは、焦点面で10mmの視野絞りに10組の白黒のラインの組を見ているので、空間周波数
=1lp/mmとなり、この望遠鏡は空間周波数を変えない等倍の望遠鏡ということになります。
・従ってコントラストも元の1.0となります。これは下の図のように、MTFチャートの左上端(コント
ラスト=1.0)により表現されます。
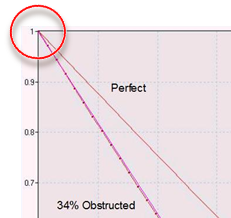
1.3 倍率を上げると
・10組/10mmのテストチャートを下図のように600組/10mmの細かいテストチャートに置換えると、
等倍では分解できません。;
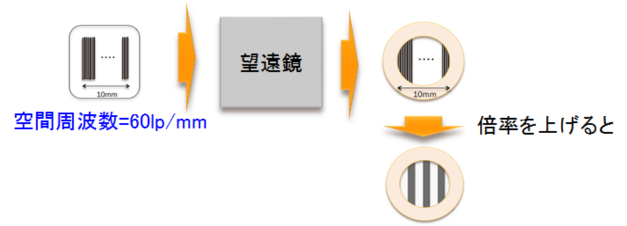
・倍率を上げると、コントラストが低下しますが像は拡大されて見えます(図では、600組/10mm→
3組/10mmに拡大しているのでその倍率=600/3=200倍)。
→どの位まで細かいテストチャートを見ることができるでしょうか?
1.4 最大空間周波数
・「どの位細かいテストチャートを見ることができるか?」
という問題は、「識別可能な白黒の最大空間周波数」を求めることに帰着します。
・これをSLで表すと、SLは下記式で求まります;(H. Rutten & M. van Venrooij, TELESCOPE
OPTICS P.205より)
■望遠鏡の口径をD(mm), 焦点距離をf(mm), 光の波長をλ(mm)とすると、
SL=D/(f*λ)=1/((f/D)*λ) :単位はlp/mm
→SLは焦点比(f/D)とλで決まります。
(例)焦点比(f/D)=10, λ=555nm=555*10-4mm(グリーン光)とすると、
SL=1/(10*555*10-4)=180lp/mm
この場合、1mm当り最大180組の白黒ラインを識別します。
・空間周波数を考える範囲を長さ(mm)でなく角度で考えると、それはある単位角内の白黒
の組の数となります。
Star Testingの本では、「白黒の組の数」をサイクルと呼んでいるので、角度で空間周波数
を考える場合は「サイクル」を使用するようにします。
■望遠鏡の口径をD(mm), 光の波長をλ(mm)とすると、空間周波数の最大値Smaxは下記の
式で求まります;
Smax=D/λ[サイクル/radian]=(D/λ)*(π/180)*(1/3600)[サイクル/秒角]
(例)D=100mm,λ=550/1000000mmの場合、
Smax=182000[サイクル/radian]=0.88[サイクル/秒角]
※Smaxは口径に依存し、焦点比とは独立です。
上記より、
Smax=182000[サイクル/radian]=0.88[サイクル/秒角]
それでは、このSmaxの逆数1/Smaxは何を意味するだろうか?
■1/Smax=1/0.88=1.14秒角/サイクル
→これは白黒(明暗)を区別する最小の角度であり、角分解能を意味します。この値は、
口径10cmのドーズのリミットである1.16秒角より少し小さな値です。
2.How to understand an MTF Chart...要点紹介
2.1 評価する望遠鏡
MTFチャートを説明するために下記の3種類の望遠鏡が使用されている;
①口径D=8インチ、焦点比f/D=10の完全な無遮蔽望遠鏡
②口径D=8インチ、焦点比f/D=10、遮蔽率34%の中央遮蔽望遠鏡
③口径が①、②の60%で焦点比f/D=10の完全な無遮蔽望遠鏡
・焦点比f/D=10の望遠鏡の「識別可能な白黒の最大空間周数」SLは、1.4節から
SL=1/(10*555*10-4)=180lp/mm
となります。MTFチャートでは、これを正規化して
MTFチャートのx軸の最大値1.0⇔180lp/mm
と対応させます。
2.2 問題の設定
【使用する解像力テストチャート】
最初に、空間周波数=60lp/mmのテストチャートを使用する。

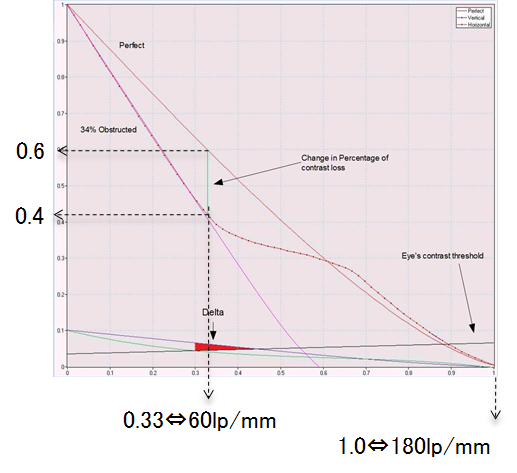
空間周波数=60lp/mmは①②の望遠鏡の極限分解能である180lp/mmの33%に対応します。
従って、極限分解能の180lp/mmを正規化して「1.0」とすると、60lp/mmは0.33です(MTFのチャート
からこのポイントでの「完全な」望遠鏡のMTFラインは左軸の0.6に位置します)。
→次節のMTFチャート参照。
2.3 MTFチャートの見方
・下の図のperfectのラインは①の望遠鏡のMTFです。
・34%遮蔽のラインは②の望遠鏡のMTFです。
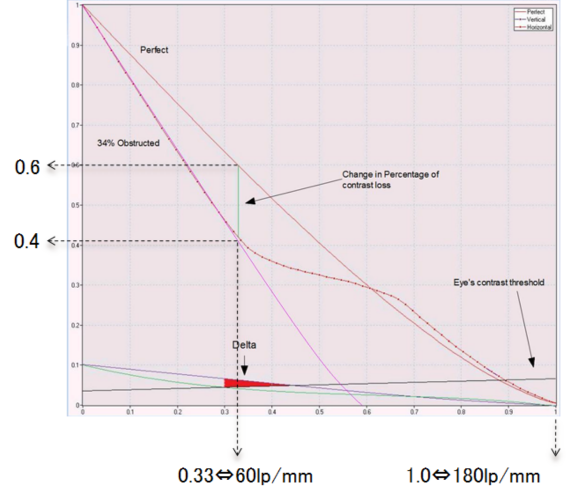
【破線の説明】
今、対象を望遠鏡で見たとき焦点面でサイズが60lp/mmだったとします。
このとき、対象のコントラストがたとえ100%でも、60lp/mmを分離できる最小の倍率でそれを
見たときには、アイピース側では①の望遠鏡はコントラストが60%に低下し、②の望遠鏡はなんと
40%まで低下しているということです! このとき、ラインはもはや完全な黒や白には見えません。
上記の内容を纏めると、
「X軸=0.33のポイントでは、無遮蔽でも遮蔽有でもどちらの望遠鏡でも、(見る対象のコントラストが
非常に良いならば)対象の詳細を完全に見ることができます! しかし、無遮蔽の望遠鏡は、中央
遮蔽の望遠鏡よりもコントラストが良く白黒のラインを僅かにシャープでより目立つようになるという
違いがあります。対象の詳細は中央遮蔽の望遠鏡では少し色あせますが、対象は見えています。」
次に、空間周波数=120lp/mmの対象を見た場合について考えてみます;
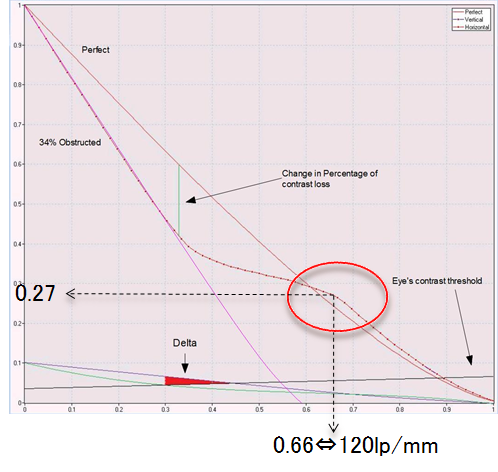
「120lp/mmの空間周波数は①②の望遠鏡の極限分解能である180lp/mmの66%なので、
正規化された値はX軸の0.66のポイントになります。
MTFのチャートを見ると、このポイント付近では中央遮蔽のMTFラインは無遮蔽のラインと
クロスしそれを越えています。
従って、この周波数では、②の望遠鏡は①の望遠鏡より実際に少し性能が良くなります。」
「しかし、0.66のポイントでは①と②のどちらの望遠鏡でもコントラストが失われ始めていること
に注目して下さい。X軸=0.66においては、対象のコントラストがたとえ100%でもアイピース側
ではコントラストが27%しかありません。」
今までは対象のコントラストは100%(完全な白と黒)の場合でしたが、
今度は「MTFチャートの縦軸の0.1(10%のコントラスト)でスタートする2つのライン」を調べます。
「これは、下図の下の方の紫のラインは無遮蔽の①の望遠鏡を表しています。青緑のラインは
中央遮蔽の②の望遠鏡を表しています。真直ぐな黒いラインは人間の眼がコントラストを
認識可能な最小のしきい値を表しています。
このケースでは、10%のコントラストしか持たない対象上の白黒のラインでスタートします。
それらは同じようなグレーの影に非常に近いラインとして現れます。」
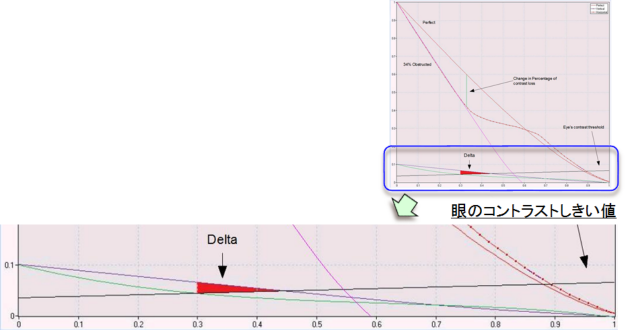
「青緑のラインが眼のコントラストのしきい値と交差するポイント(X軸の0.3)では、もはや詳細は
見えなくなります。」
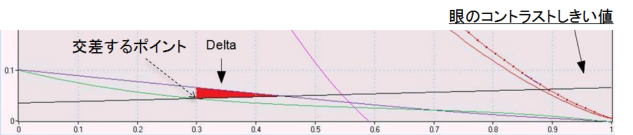
「図中の赤い三角形(Delta)は、中央遮蔽の望遠鏡では見えないが無遮蔽の望遠鏡では見える
領域を表しています! 青緑のラインが「眼のコントラストのしきい値」と交差するポイント(X軸の
0.3)の左側にある細部は、中央遮蔽の望遠鏡では見るのが難しくなりますが、(眼のコントラスト
のしきい値より上の領域なので)観測者はまだそれを見ることができます!!!」
→このように、対象の詳細のコントラストが低いほど中央遮蔽の望遠鏡は詳細が見えなくなります。
2.4 具体的な天体の事例:木星
【木星観測の状況説明】
「①、②の望遠鏡を使用して、10mmの視野絞りを持つアイピースを使用し、木星がこの望遠鏡
のアイピースの見かけの視野の1/10を占めていたとします。」
→木星の見かけの大きさが10mmの視野絞りの10%なので、これは1lp/mmの白黒のラインの1組
と同じスペースを占めます(下の図)。
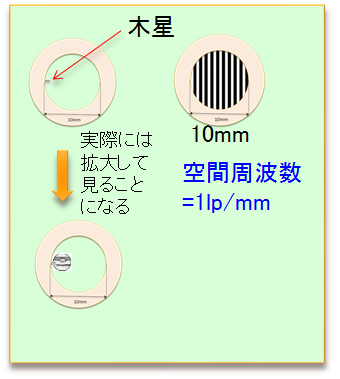
したがって、「この望遠鏡に対して木星は空間周波数1に相当します。」
ここで、衛星の影の木星面通過の状況を考えます。
・「木星面の衛星の影の通過では、その影は木星本体の直径の1/60と言われているので、
衛星の影の空間周波数は60LPPMです。」
・衛星の影は非常に高いコントラストの状態から出発すると考えて良いので、遮蔽と無遮蔽
の2つの望遠鏡はどちらもそれを容易に見ることができます。(分解能180lp/mmの望遠鏡
で60lp/mmを見るためにはX軸=0.33なので、)
このとき、衛星の影のコントラストは無遮蔽の望遠鏡で60%に低下し、中央遮蔽の望遠鏡
では44%に低下しています。
それでもコントラストはまだ高い方なので中央遮蔽の望遠鏡でも衛星の影は黒く見えますが、
実際には非常に暗いグレーです。
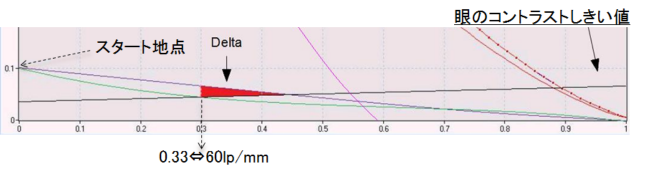
・上記の例は明るい木星面のコントラストの高い衛星の影の話でした。
・しかし、衛星の影と同じサイズ(空間周波数60LPPM)の木星の楕円模様が非常に低いコント
ラスト(例:10%)でスタートしたら、MTFチャートよりそれは赤い三角形の領域に入り、中央遮蔽
の望遠鏡では見えなくなりますが、無遮蔽の望遠鏡はまだ「眼のコントラストのしきい値」より
上にあります。
・さらに、木星の微かなフェストーンは僅か5%か6%のコントラストからスタートします。それらは
非常に大きくなければ、無遮蔽の望遠鏡で見えているのに中央遮蔽の望遠鏡では見ることが
できないことになります。
・衛星の木星面通過で衛星の影でなく衛星そのものを見る場合、木星本体と衛星のコントラスト比
は小さいので、MTFチャートは低コントラストからスタートします。
2.5 3番目の望遠鏡について
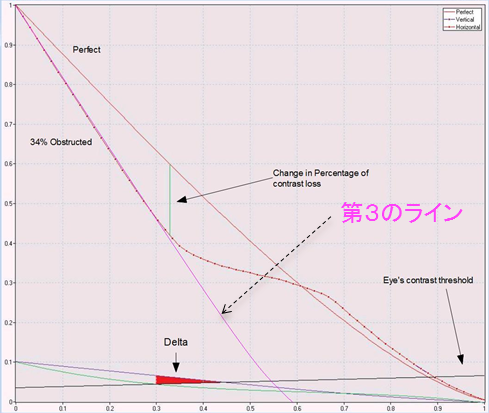
・MTFの左上端に始まる第3のラインがあることに注目して下さい。
このラインは無遮蔽の「より小さな望遠鏡③」を表しています。このラインはX軸の0.6のポイント
で終わっています。
・これは、他の2つの望遠鏡の60%の大きさの口径を持つことを示唆しています(60%の分解能しか
ないので)。これは、②という8インチの中央遮蔽の望遠鏡を無遮蔽の望遠鏡に近似的に換算した
もの(口径約60%)と考えられる。
【③の望遠鏡の特徴】
・第一に、最も大きく、最もコントラストの高い詳細に対しては小さな望遠鏡のMTFラインは(大きな
中央遮蔽と)同様ですが、最も細かな詳細の解像力に関しては大きな2つの望遠鏡にはるかに
及びません。
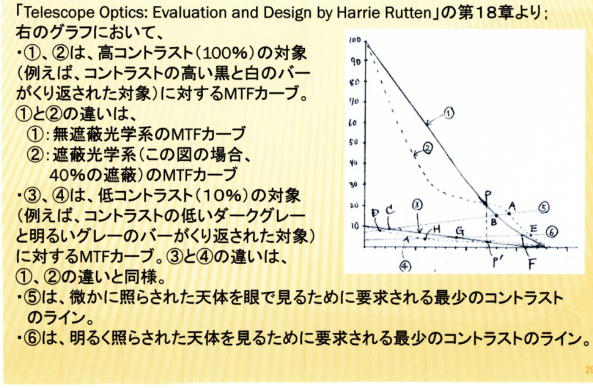
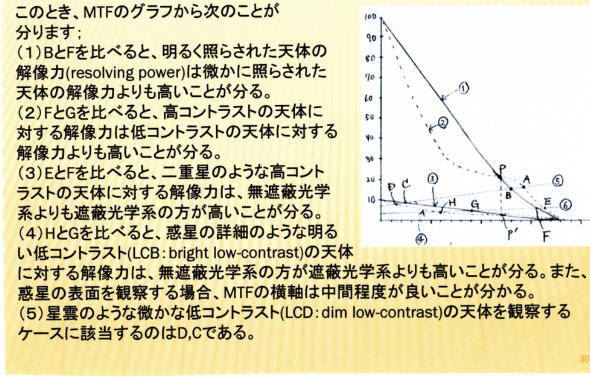
(参考)Harrie Rutten他著「Telescope Optics: Evaluation and Design」のMTF
の説明紹介
How to understand an MTF chart...の内容紹介)
(*)http://www.cloudynights.com/ubbthreads/showflat.php/Cat/0/Number/4415334/page/0/
view/collapsed/sb/5/o/all/fpart/all/vc/1
2014年3月作成:舟越 和己
Cloudy Nightsの上記のMTFについての説明は非常に良い内容です。
以下ではこれを図解にして簡単に紹介します。
1.準備(予備知識)
1.1 解像度テストチャート
・下の図のような各々0.5mmの幅の白と黒のラインが交互に繰り返している解像力テストチャート
を考えます。

・このチャートは、1mmの幅に「白黒ラインの組」が1組あり、全体で10組の「白黒ラインの組」から
構成されています。
・また、このテストチャートは、完全な白と完全な黒、すなわち白の強度=10, 黒の強度=0とします。
このとき、
Modulation=(10-0)/(10+0)=1.0
なので、そのコントラストは100%です。
・一般に、1mmあたりの白黒ラインの組の数をlp/mm(Line pairs per millimeter)と言います。
→下の図①では、1mmあたり1組なので1lp/mmです。
また、下の図②のように、1mmあたり60組の白黒ラインの組があれば、これは60lp/mmです。

・白黒ラインの1組が正弦波の1波長に該当します。(このため「白黒ラインの1組」を1サイクルと
呼ぶこともあります)
→上の図の①は1波長=1mm, ②は1波長=1/60mm
従って、
「1ミリあたりの白黒ラインの組の数=1/波長
=空間周波数(Spatial Frequency)」が成立する(重要!)
→右図の①の空間周波数=1lp/mm, ②の空間周波数=60lp/mm
※空間周波数は角度で考える場合もある。→後で説明有。
1.2 等倍の望遠鏡
・下の図のように望遠鏡に10mmの視野絞りを持つアイピースを入れて、その望遠鏡で解像力
テストチャートを見たときに10組ラインになるようにチャートを望遠鏡の前方に置く。

・これは、焦点面で10mmの視野絞りに10組の白黒のラインの組を見ているので、空間周波数
=1lp/mmとなり、この望遠鏡は空間周波数を変えない等倍の望遠鏡ということになります。
・従ってコントラストも元の1.0となります。これは下の図のように、MTFチャートの左上端(コント
ラスト=1.0)により表現されます。

1.3 倍率を上げると
・10組/10mmのテストチャートを下図のように600組/10mmの細かいテストチャートに置換えると、
等倍では分解できません。;

・倍率を上げると、コントラストが低下しますが像は拡大されて見えます(図では、600組/10mm→
3組/10mmに拡大しているのでその倍率=600/3=200倍)。
→どの位まで細かいテストチャートを見ることができるでしょうか?
1.4 最大空間周波数
・「どの位細かいテストチャートを見ることができるか?」
という問題は、「識別可能な白黒の最大空間周波数」を求めることに帰着します。
・これをSLで表すと、SLは下記式で求まります;(H. Rutten & M. van Venrooij, TELESCOPE
OPTICS P.205より)
■望遠鏡の口径をD(mm), 焦点距離をf(mm), 光の波長をλ(mm)とすると、
SL=D/(f*λ)=1/((f/D)*λ) :単位はlp/mm
→SLは焦点比(f/D)とλで決まります。
(例)焦点比(f/D)=10, λ=555nm=555*10-4mm(グリーン光)とすると、
SL=1/(10*555*10-4)=180lp/mm
この場合、1mm当り最大180組の白黒ラインを識別します。
・空間周波数を考える範囲を長さ(mm)でなく角度で考えると、それはある単位角内の白黒
の組の数となります。

Star Testingの本では、「白黒の組の数」をサイクルと呼んでいるので、角度で空間周波数
を考える場合は「サイクル」を使用するようにします。
■望遠鏡の口径をD(mm), 光の波長をλ(mm)とすると、空間周波数の最大値Smaxは下記の
式で求まります;
Smax=D/λ[サイクル/radian]=(D/λ)*(π/180)*(1/3600)[サイクル/秒角]
(例)D=100mm,λ=550/1000000mmの場合、
Smax=182000[サイクル/radian]=0.88[サイクル/秒角]
※Smaxは口径に依存し、焦点比とは独立です。
上記より、
Smax=182000[サイクル/radian]=0.88[サイクル/秒角]
それでは、このSmaxの逆数1/Smaxは何を意味するだろうか?
■1/Smax=1/0.88=1.14秒角/サイクル
→これは白黒(明暗)を区別する最小の角度であり、角分解能を意味します。この値は、
口径10cmのドーズのリミットである1.16秒角より少し小さな値です。
2.How to understand an MTF Chart...要点紹介
2.1 評価する望遠鏡
MTFチャートを説明するために下記の3種類の望遠鏡が使用されている;
①口径D=8インチ、焦点比f/D=10の完全な無遮蔽望遠鏡
②口径D=8インチ、焦点比f/D=10、遮蔽率34%の中央遮蔽望遠鏡
③口径が①、②の60%で焦点比f/D=10の完全な無遮蔽望遠鏡
・焦点比f/D=10の望遠鏡の「識別可能な白黒の最大空間周数」SLは、1.4節から
SL=1/(10*555*10-4)=180lp/mm
となります。MTFチャートでは、これを正規化して
MTFチャートのx軸の最大値1.0⇔180lp/mm
と対応させます。
2.2 問題の設定
【使用する解像力テストチャート】
最初に、空間周波数=60lp/mmのテストチャートを使用する。

空間周波数=60lp/mmは①②の望遠鏡の極限分解能である180lp/mmの33%に対応します。
従って、極限分解能の180lp/mmを正規化して「1.0」とすると、60lp/mmは0.33です(MTFのチャート
からこのポイントでの「完全な」望遠鏡のMTFラインは左軸の0.6に位置します)。
→次節のMTFチャート参照。
2.3 MTFチャートの見方
・下の図のperfectのラインは①の望遠鏡のMTFです。
・34%遮蔽のラインは②の望遠鏡のMTFです。

【破線の説明】
今、対象を望遠鏡で見たとき焦点面でサイズが60lp/mmだったとします。
このとき、対象のコントラストがたとえ100%でも、60lp/mmを分離できる最小の倍率でそれを
見たときには、アイピース側では①の望遠鏡はコントラストが60%に低下し、②の望遠鏡はなんと
40%まで低下しているということです! このとき、ラインはもはや完全な黒や白には見えません。
上記の内容を纏めると、
「X軸=0.33のポイントでは、無遮蔽でも遮蔽有でもどちらの望遠鏡でも、(見る対象のコントラストが
非常に良いならば)対象の詳細を完全に見ることができます! しかし、無遮蔽の望遠鏡は、中央
遮蔽の望遠鏡よりもコントラストが良く白黒のラインを僅かにシャープでより目立つようになるという
違いがあります。対象の詳細は中央遮蔽の望遠鏡では少し色あせますが、対象は見えています。」
次に、空間周波数=120lp/mmの対象を見た場合について考えてみます;

「120lp/mmの空間周波数は①②の望遠鏡の極限分解能である180lp/mmの66%なので、
正規化された値はX軸の0.66のポイントになります。
MTFのチャートを見ると、このポイント付近では中央遮蔽のMTFラインは無遮蔽のラインと
クロスしそれを越えています。
従って、この周波数では、②の望遠鏡は①の望遠鏡より実際に少し性能が良くなります。」
「しかし、0.66のポイントでは①と②のどちらの望遠鏡でもコントラストが失われ始めていること
に注目して下さい。X軸=0.66においては、対象のコントラストがたとえ100%でもアイピース側
ではコントラストが27%しかありません。」
今までは対象のコントラストは100%(完全な白と黒)の場合でしたが、
今度は「MTFチャートの縦軸の0.1(10%のコントラスト)でスタートする2つのライン」を調べます。
「これは、下図の下の方の紫のラインは無遮蔽の①の望遠鏡を表しています。青緑のラインは
中央遮蔽の②の望遠鏡を表しています。真直ぐな黒いラインは人間の眼がコントラストを
認識可能な最小のしきい値を表しています。
このケースでは、10%のコントラストしか持たない対象上の白黒のラインでスタートします。
それらは同じようなグレーの影に非常に近いラインとして現れます。」

「青緑のラインが眼のコントラストのしきい値と交差するポイント(X軸の0.3)では、もはや詳細は
見えなくなります。」

「図中の赤い三角形(Delta)は、中央遮蔽の望遠鏡では見えないが無遮蔽の望遠鏡では見える
領域を表しています! 青緑のラインが「眼のコントラストのしきい値」と交差するポイント(X軸の
0.3)の左側にある細部は、中央遮蔽の望遠鏡では見るのが難しくなりますが、(眼のコントラスト
のしきい値より上の領域なので)観測者はまだそれを見ることができます!!!」
→このように、対象の詳細のコントラストが低いほど中央遮蔽の望遠鏡は詳細が見えなくなります。
2.4 具体的な天体の事例:木星
【木星観測の状況説明】
「①、②の望遠鏡を使用して、10mmの視野絞りを持つアイピースを使用し、木星がこの望遠鏡
のアイピースの見かけの視野の1/10を占めていたとします。」
→木星の見かけの大きさが10mmの視野絞りの10%なので、これは1lp/mmの白黒のラインの1組
と同じスペースを占めます(下の図)。

したがって、「この望遠鏡に対して木星は空間周波数1に相当します。」
ここで、衛星の影の木星面通過の状況を考えます。
・「木星面の衛星の影の通過では、その影は木星本体の直径の1/60と言われているので、
衛星の影の空間周波数は60LPPMです。」
・衛星の影は非常に高いコントラストの状態から出発すると考えて良いので、遮蔽と無遮蔽
の2つの望遠鏡はどちらもそれを容易に見ることができます。(分解能180lp/mmの望遠鏡
で60lp/mmを見るためにはX軸=0.33なので、)
このとき、衛星の影のコントラストは無遮蔽の望遠鏡で60%に低下し、中央遮蔽の望遠鏡
では44%に低下しています。
それでもコントラストはまだ高い方なので中央遮蔽の望遠鏡でも衛星の影は黒く見えますが、
実際には非常に暗いグレーです。

・上記の例は明るい木星面のコントラストの高い衛星の影の話でした。
・しかし、衛星の影と同じサイズ(空間周波数60LPPM)の木星の楕円模様が非常に低いコント
ラスト(例:10%)でスタートしたら、MTFチャートよりそれは赤い三角形の領域に入り、中央遮蔽
の望遠鏡では見えなくなりますが、無遮蔽の望遠鏡はまだ「眼のコントラストのしきい値」より
上にあります。

・さらに、木星の微かなフェストーンは僅か5%か6%のコントラストからスタートします。それらは
非常に大きくなければ、無遮蔽の望遠鏡で見えているのに中央遮蔽の望遠鏡では見ることが
できないことになります。
・衛星の木星面通過で衛星の影でなく衛星そのものを見る場合、木星本体と衛星のコントラスト比
は小さいので、MTFチャートは低コントラストからスタートします。
2.5 3番目の望遠鏡について

・MTFの左上端に始まる第3のラインがあることに注目して下さい。
このラインは無遮蔽の「より小さな望遠鏡③」を表しています。このラインはX軸の0.6のポイント
で終わっています。
・これは、他の2つの望遠鏡の60%の大きさの口径を持つことを示唆しています(60%の分解能しか
ないので)。これは、②という8インチの中央遮蔽の望遠鏡を無遮蔽の望遠鏡に近似的に換算した
もの(口径約60%)と考えられる。
【③の望遠鏡の特徴】
・第一に、最も大きく、最もコントラストの高い詳細に対しては小さな望遠鏡のMTFラインは(大きな
中央遮蔽と)同様ですが、最も細かな詳細の解像力に関しては大きな2つの望遠鏡にはるかに
及びません。
(参考)Harrie Rutten他著「Telescope Optics: Evaluation and Design」のMTF
の説明紹介

