Diffraction pattern of aperture with central obstraction

　　　　　　　　　　　　　　　　　　　　　　　9/26/2017   K. Funakoshi

■What is central obstraction

　　The central obstraction (of astronomical telescope) is circular shield existing on the aperture
 of telescope. Concretely, it is relevant to the secondary mirror of reflector or ctadioptric.　

           

　　　　　　　　　　　　　　　　　

　　εis relative size of central obstraction of D
    In most amature telescopes, ε is in the 0.2D to 0.5D.

　We consider following 3 type apertures to understand the diffraction pattern of aperture with
central obstraction.

     

 

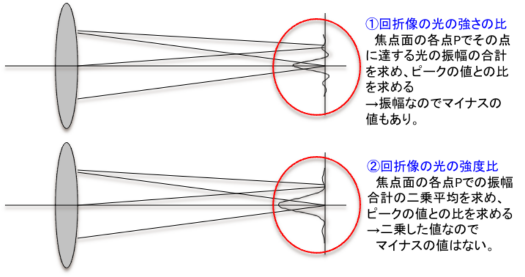
　■ 　2 type mathematical representations of deffraction pattern from diffraction theory.

　　(1) One representation use the amplitude of light at P ( P is the point on the focal plane)
        i. e. When P is any point on the focal plane,  we considerΣ(amplitude of lights at P)).
             This is summation of all amplitude of lights to reach the point P from aperture.
             Then, there is a peak value of Σ(amplitude of lights at P)). usually this point is
             focal point.
             And therefor, one mathematical representaion of deffraction pattern is
             rarion of Σ(amplitude of lights at P)) and peak value of Σ(amplitude of lights at P)).

   (2) The other representation use the mean square of amplitudes of light at P.
。　   i. e. ratio of (mean square value of amplitudes of light at P) and
            peak value of (mean square value of amplitudes of light at P).

     

 

　■Relation between size of aperture and diffractin pattern

　 Light intensity(amplitude) weakens and the size of diffraction pattern increase in size,
  the smaller the aperture;

     

 

　■What is complementary to each other shading？

　　It is a shading that transparent portion and opaque portion are reversal, as following figure;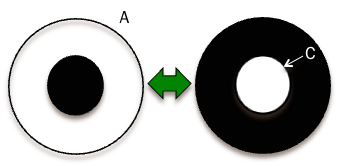      

 

　■Babinet's principle；

　For complementary screens is that the sum of the wave transmitted through a screen
 (usually considered to be “black” except for its apertures), plus the wave transmitted
 through the complementary screen, is the same as if no screen were present.

　⇒Therefor, following fact is established;

　●amplitude of diffracted ligh by obstracted aperture
    = ( amplitude of diffracted light by unobstracted aperture)
       - (amplitude of diffracted light by same size of aperture
                                              as obstract)

 ■example  The following figure is shown above fact.
　　

     

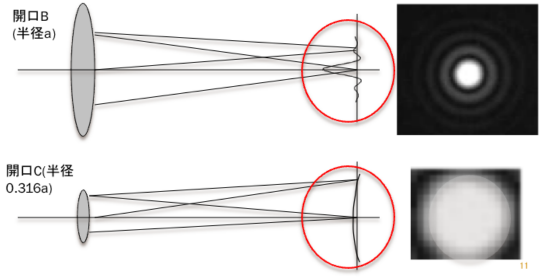
Expand the circled in red. The numerical values in Fig. show the amplitude of diffraction light.

       

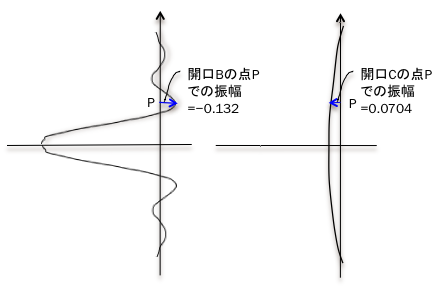
  the difference of amplitudes = -0.132-0.0704=0.2024

As in this example, absolute value of the difference of amplitudes may be larger than the
absolute value of the amplitude of aperture B.
→Reason that first diffraction ring of central obstracted optics is brighter than that of
  unobstracted optics is here.

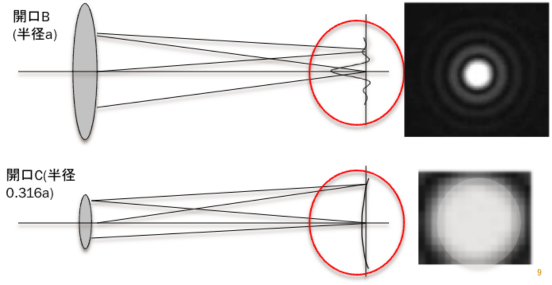
■Distribution of diffracted light intensity of aperture B and C.

 Figure on the left below is amplitude distribution of diffracted light from aperture B.
 Figure on the right below is amplitude distribution of diffracted light from aperture C.

　■diffraction as minus

   amplitude of diffracted ligh by obstracted aperture
    = ( amplitude of diffracted light by unobstracted aperture)
       - (amplitude of diffracted light by same size of aperture as obstract)

   =( amplitude of diffracted light by unobstracted aperture)
       + (- (amplitude of diffracted light by same size of aperture as obstract))

  Here, - (amplitude of diffracted light by same size of aperture as obstract) is called
  diffraction as minus.

　

 

　■How to obtain diffracted pattern of central obstracted aperture.

　　
   This ic calculated as folows;
   { ( amplitude of diffracted light by unobstracted aperture)
       + (- (amplitude of diffracted light by same size of aperture as obstract)) }²

　

　

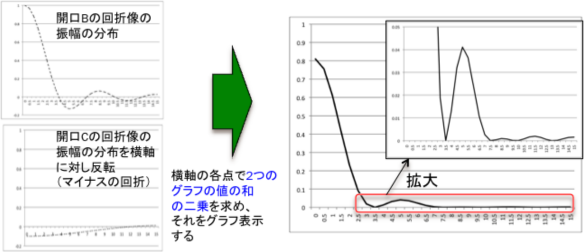
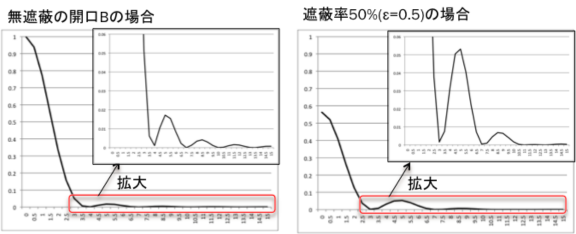
■ Based on the above results, we compare intensities of diffracted pattern of unobstructed
   and obstructed(ε=0.316) case.　

　

 　→From two figures, we can see that first diffraction ring of central obstracted optics is
      brighter than that of unobstracted optics.

　■ If ε=0.5, the intensity of first diffraction ring is increase further.