eye aberration

眼の球面収差について

　　　　　　　　　　　　　　　　　　　　　　　２０１７年１２月　舟越　和己

眼の球面収差について調べたことを纏めてみました。

１．眼の球面収差についての情報

　一般にスターテストの本の球面収差は高倍率での評価が中心ですが、下記に眼の球面収差
の関する情報がありました；

　　●Notes on AMATEUR TELESCOPE OPTICSの13.5. HIGHER ORDER MONOCHROMATIC

　　EYE ABERATIONS（高次単色の眼の収差）

　　　http://www.telescope-optics.net/higher_order_eye_aberrations.htm

この情報を説明する前に球面収差についての説明をします。
球面収差の焦点には下記の種類があります；

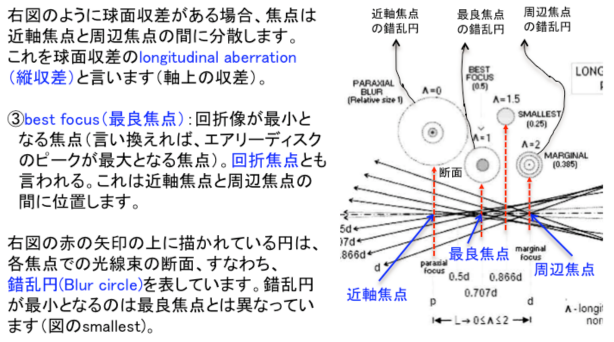
２．HIGHER ORDER MONOCHROMATIC EYE ABERATIONS（高次単色の眼の収差）の概要

　光学系の球面収差は参照波面の中心をどこに置くかにより変わりその様子は下の図の
　ようになります；

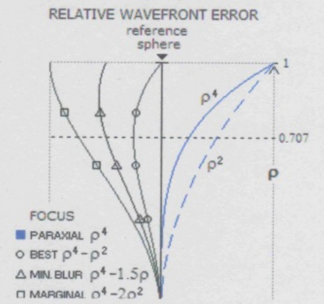
例えば、近軸焦点を参照波面の中心にすると、下の図のように球面収差関数はミラーの
半径ρの関数として、４次の項のみとの４次関数になります。この場合のP-V波面収差は
図の右の通りです。

一方、最良焦点を参照波面の中心にすると、下の図のように球面収差関数はミラーの
半径ρの関数として、４次と２次の項を持つ４次関数。この場合のP-V波面収差は図の
右のように、近軸焦点を参照波面とした場合に較べてかなり小さな値になります。

それでは参照波面を「近軸焦点」から「最良焦点」に移動させた場合、球面収差の値が
どの程度減少するかについては一般論から下の図のようなグラフがあります。

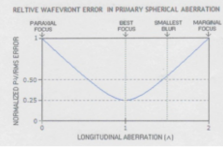
この図を見ると近軸焦点(PARAXAL)→最良焦点(BEST)に調節することにより約0.25=1/4
程度収差が減少することが分かります。

眼は瞳孔が開いたとき、球面収差により近軸焦点で対象を見るこのとになるので、眼の球面
収差の光学精度（P-V値やRMS値）は近軸焦点を参照波面の中心として求めることになります。

HIGHER ORDER MONOCHROMATIC EYE ABERATIONS（高次単色の眼の収差）では、これを
次の手順でラフな値を求めています；

　①眼の球面収差の縦収差の平均値を眼科のデータ（ディオプター値）から得る。

　②眼の縦収差が分かると、収差関数の議論から最良焦点にピントを合わせたときの球面収差の

　　　P-V波面収差値Wsが求まる。

　③P-V波面収差からRMS波面収差への一般的な変換式により、眼の球面収差のRMS値を求める。

以下、①、②、③の内容を示すと次の通り；

①眼の縦収差の値については学会でも意見の相違がある（実測値と波面収差から得られる値
の差異など）が、ここでは瞳孔径=6mmのとき平均値として-1D（ディオプター）を採用しています。
これは、夜間に瞳孔が6mmまで開いたとき、裸眼視力が0.5まで近視になることを示しています。
また、-1Dということは正常な眼の焦点距離fE=17mmとするとき、縦収差Ls=0.28mmであること
が見積もれます（詳細は書かれていない）。

②球面収差のP-V波面収差値Wsは縦収差Lsに比例し下記の式で表せます。

　　　　　　　Ws=Ls/64F² （Fは焦点比：F=f_E/P）

眼の場合、f_E=17mmとしているので

　　　　　　　Ws=Ls/(64F² )=LsP²/(64f_E)= LsP²/(64*17)= LsP²/(18,500)　・・・(1)

縦球面収差は直径の二乗に比例するのでP=6mmのf_E値, Ls値から

　　　　　　　Ls ≒ f_E(P/6)²/60

という近似式が類推でき、f_E=17mmとして(1)式に代入すると、

　　　　　　　Ws = LsP²/(18,500)≒17*P⁴/(18,500*36*60)=P⁴/2,350,000

Wsの単位はmmなのでこれを光の波長の単位(λ=0.55μm)に置換えると、

　　　　　　　Ws=(P⁴/2,350,000)*(0.55*1000) ≒ P⁴/1300

すなわち、収差理論から瞳孔径のサイズP(mm)と眼の最良焦点での球面収差の関係は、

P-V波面収差として

　　　　　　　Ws=P⁴/1300（単位はλ）

これは開口Pの４次のみの式なので確かに近軸の波面収差になっています。

③RMS球面収差への変換は1/SQRT(11.25)（注）を掛けることにより求めます。

従って、RMS波面収差として

　　　　　　　　Ws=P⁴/4334（単位はλ）

が得られます。

（注）Suiter著のStar Testingの本では、PーV波面収差＝λ/4　⇔　RMS波面収差＝λ/14

　　　の対応があると書かれています。すなわち、近似的には下記；

　　　　　　　PーV波面収差≒3.5×RMS波面収差

以上から、瞳孔径P=6mmの場合、眼の球面収差はP-V波面収差で64/1300≒1λ（RMS波面
収差では64/4334≒1/3λ）となる。ディフラクションリミット（P-V波面収差=1/4λ）となる瞳孔径
のサイズはP⁴/1300=1/4からP≒4.2mmとなる。3mmの瞳孔径ではエラーはすでにディフラクション
リミットレベルに達しているので完全に無視できます。

→この結果についてさらに次のように述べられています；

「Again, it may be only a rough average, not only because of disagreements in experimental
measurements, but also due to eye's varying levels of adjustment. However, it seems safe
to conclude that spherical aberration of the eye is unlikely to be significant factor in observing
with a telescope. It may be relatively significant at large pupil sizes, but it is inconsequential,
for two reasons: it is still significantly lower than other axial aberrations of the eye, and low
magnifications associated with large (eyepiece) pupils are insufficient to make its effect on
image quality perceptible.（これは実験的測定結果での異論だけでなく、眼のさまざまな適応レベル
の理由により、あくまでもラフな平均値に過ぎない。しかし、望遠鏡で天体を観察する場合において
眼の球面収差が重要なファクターにはなりそうにもないと結論付けても良いと思われる。眼の球面
収差は比較的大きな瞳径で重要になるが、２つの理由によりそれは取るに足らない：それは眼の
他の軸上収差（焦点ズレ等）より遥かに小さく、大きな（アイピース）瞳径に関係する低倍率では
像質に認知できるような影響を与えるには不足している）」

→最後の文章の意味についてその理由を考えてみます。

　まず、上記で求めた眼の球面収差Wsは焦点調節が難しい眼の構造から「近軸焦点」を参照
波面とした収差の値です。一方、望遠鏡を通して星を見る場合、望遠鏡による焦点調節により
眼の球面収差の最良焦点にピントを合わせることができるので、眼の球面収差の光学精度
（P-V値やRMS値）は参照波面の中心を「最良焦点」として求めることになります。参照波面を
「近軸焦点」から「最良焦点」に移動させた場合、約0.25=1/4程度収差が減少することが分かって
いるので、「瞳孔径P=6mmの場合、眼の球面収差はP-V波面収差で1λ*0.25=1/4λ（RMS波面
収差では1/3λ*0.25=1/12λ）」となります。これはディフラクションリミテッドの値です。低倍率
でも眼の収差の影響はあまりないというのはこのためではないかと思われます。

これを球面収差のMTF図で示すと次のようになります；

上の図の説明：これは高コントラスト(100%)な天体を見た場合の球面収差によるコントラスト
の低下を示しています。球面収差の値はP-V波面収差。縦軸はModulation transfer, 横軸は
正規化された空間周波数です。

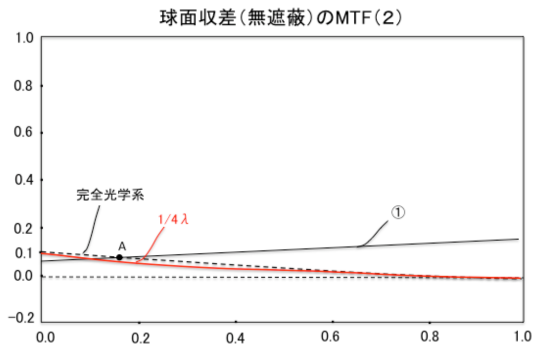
次に、次の図は低コントラスト(10%)の天体を見た場合の球面収差によるコントラストの低下
を示しています。

①は微かに照らされた天体を眼で見るために要求される最少のコントラストのラインです（この
ライン以下のコントラストの天体は見ることができない）。点Aは低コントラストの天体（淡い星雲
など）を完全光学系で見た場合に見分ける事ができる限界です。したがって、完全光学系のMTF
≧ ①のラインの範囲ならばその望遠鏡は低倍率でコントラスト10%の天体を見分けることができ
ます。一方、球面収差=1/4λのMTF（赤のカーブ）はわずかに完全光学系のMTFのラインより下
なので、非常に淡い天体を見るときに少し差がでるがその差は非常に小さい。

点Aの付近を拡大すると、下の図のようになります。ここで、赤い三角形(Delta)は、1/4λでは
見えないが完全光学系では見える領域を表しています。

３．（望遠鏡+眼）トータルの収差について

　私のHP（4インチ屈折の世界）の「光学精度のこと（続き）」

http://www2.odn.ne.jp/~ccr61210/www2.odn.ne.jp/seido2.html

において独立事象での正規分布の合成により、トータルシステムとしてのRMS波面収差を議論
しました。この考え方を適用して望遠鏡の球面収差RMS_lensと眼の球面収差RMS_eyeの合成
RMS_Totalを求めます；

　　　　　　　RMS_Total²＝RMS_lens²＋RMS_eye²

　　　　　　　つまり、

　　　　　　　RMS_Total＝SQRT（RMS_lens²＋RMS_eye²）

　　　　　　　（ここで、SQRTは平方根を意味します。）

となります。

（例１）１台目は、球面収差RMS_lens＝1/１0λの望遠鏡

　　　→PーV波面収差＝1/4λ　⇔　RMS波面収差＝1/14λなので、この場合、PーV波面
収差＝1/4λをやや下回る。つまり、ディフラクションリミテッドにやや未達とします。

　　　２台目は、球面収差RMS_lens＝1/３５λの望遠鏡（高精度）

　　　両方とも低倍率で瞳孔径=6mmで天体を見ているとします。すなわち、眼のRMS球面
収差=1/12λ

　　＜１台目＞

　　　　RMS_Total＝SQRT（(1/10)²＋(1/12)²）≒1/8λ→P-V値では、1/2λ

　　＜２台目＞

　　　　RMS_Total＝SQRT（(1/35)²＋(1/12)²）≒1/11λ→P-V値では、1/3λ

　→１台目では眼の球面収差の影響が大きい。

　　このときのコントラストが低い場合のMTFチャートを見ると次のようになります。

→１台目の球面収差=1/2λの(望遠鏡+眼）のMTF（赤のカーブ）はかなりの部分①のライン
　より下なので、コントラスト10%の天体を見ることはできません。つまり、非常に淡い天体を
　見るときに差がでる。

（例２）例１と望遠鏡の条件は同じで瞳孔径=5mmで天体を見ているとします。

すなわち、眼のRMS球面収差=54/(4334*4)=1/28λ

　　＜１台目＞

　　　　RMS_Total＝SQRT（(1/10)²＋(1/28)²）≒1/13λ→P-V値では、1/3λ

　　＜２台目＞

　　　　RMS_Total＝SQRT（(1/35)²＋(1/28)²）≒1/22λ→P-V値では、1/6λ

→２台目の望遠鏡では全体の収差が1/6λと小さいので影響が見分けられないと
　　　思われる。

４．参考：夜間近視について

Sky & Telescope September 2005, SPECIAL REPORT: NIGHT MYOPIA（夜間近視）

　　http://www.skyandtelescope.com/wp-content/uploads/spectacles.pdf

に、望遠鏡や双眼鏡を使わない裸眼で星を見る場合、正常な眼の人が近視に似た状況
になる夜間近視を取り上げています。眼の球面収差は夜間近視の原因の一つです。その
状況は下の図のように、夜間は眼の瞳孔が開くことによる球面収差から最小錯乱円が焦点
よりも前に移動し、結果として像がぼやけます。

→望遠鏡と違って焦点調節が難しい？

この記事では、その対策はカスタマイズされた夜間専用の眼鏡(Stargazing Glasses)を着ける
ことだとしています。これにより最小錯乱円が眼の焦点に位置するようになるので像が改善
されるということのようです（球面収差の本質的な除去ではないが、裸眼での星の観察には
これで十分か？）。