�t���[�E�_�C�A�O�����̑� �| Dana Scott�̘_���Љ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2013�N �쐬�@�M�z�@�a��
�@�����ł́A���Ɗ��������\�t�g�E�F�A�̐��E�łǂ̂悤�ɍ\������邩�ɂ��Ă̋�̓I�C���[�W��c�����邽�߁A���������Ȃ邪�P�̗�Ƃ��ăt���[�E�_�C�A�O���������グ��B���̓��e��Dana Scott�̉��L�̘_���̊T�v�Љ�ł���G
�@�@Dana Scott: The lattice of flow diagrams�i�t���[�E�_�C�A�O�����̑��j (1970)
�P�D�t���[�E�_�C�A�O�����̕\��
�@�����I�ɁA�t���[�E�_�C�A�O�����͔��Ƀ��t�ɕ`���Ή��̐}�P�̂悤�ɂȂ�B
�@�@�@�@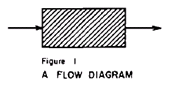
�@�@�����ɂ́A���͏���������_�ƁA�o�͂��o�Ă����o���_������B
�@���̂Ƃ��}�́h�u���b�N�{�b�N�X�h�̒��͂ǂ��Ȃ邩�Ƃ����^�₪����B
�@�@�E���̃{�b�N�X�̒��͂���ȏ㕪���ł��Ȃ����q���Z��\���Ă��邩������Ȃ����A���̃_�C�A�O����
�@�@ �Ƃ̍����ł��邩������Ȃ��B
���ɁA���̃{�b�N�X�̒��̃^�C�v���ȍ~�̐}�Q���猩�Ă����B
�@�ł��P���ȗ�͔@���Ȃ�_�C�A�O�����Ƃ̑g�������Ȃ����̂ł���B����͉��̐}�Q�́h���h�ł���B
�@�@�@�@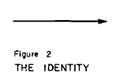
�@���̂悤�Ȗ��݂̂ɗ������͑S���ϊ�����Ȃ��G ���������āA������P����(identity function)�ŕ\���B
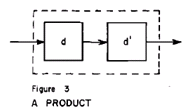
�A�����łȂ�������̈�͉��̐}�R�Ɏ�����Ă���B����́A��(product)�ƌĂ�A���̑g������
�@�����āA�ŏ��̃{�b�N�X�̏o�͂͂Q�Ԗڂ̃{�b�N�X�̓��͂�^���Ă���B
�@�@�@�@
�B�_�C�A�O�����ɂ����āA�X�C�b�`�͉��̐}�S�̂悤�ɕ\�������B
�@�@�@�@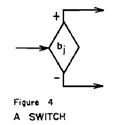
�C�X�C�b�`�̊e���Ƀ{�b�N�X���t�����A�����̃{�b�N�X�̏o�͂��ꏏ�ɂȂ�Ƃ��i���̐}�T�j�A������i�Q�̃{�b�N�X�́j�a(sum)�ƌĂ�
�@�@�@�@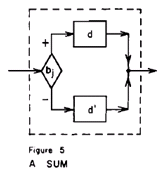
�@�ȏ�̐����̒��ŁA�a�Ɛς̓t���[�_�C�A�O�����̊�{�I�ȍ������Z�ł���B���Ȃ킿�A�����̑g�����ő傫�ȃ_�C�A�O�����������B
�Ƃ���ŁA����܂Ń��[�v�̘b���o�Ă��Ă��Ȃ����A���[�v�͌�œo�ꂷ�邱�ƂɂȂ�i���̗��R�͌�Ŗ��m�ɂȂ�B����͊������Ɩ��ڂɊW���Ă���j�B
�@�����ŁA�t���[�_�C�A�O������㐔�I�ɕ\�����邽�߂ɁA�������̕\�L���������G
�@ �E�X�C�b�`��b0, b1, b2,�E�E�E,
�@ �E�{�b�N�X��f0, f1, f2,�E�E�E,
�@ �E�_�C�A�O������d0, d1, d2,�E�E�E
�@�����ŁAb: Boolean����binary�Af: functions�Ad: diagrams���Ӗ�����B�{�b�N�X�͏���̊���\���̂�"f"���g�p�����B�_�C�A�O�����̓X�C�b�`�A�{�b�N�X�������������̂ł���B
�܂��A�P���_�C�A�O������ I�ŕ\���B
�@�����̕\�L���g�p���ă_�C�A�O�����̘a�A�ς�\������Ǝ��̂悤�ɂȂ�G
d��d'���Q�̃_�C�A�O�����̂Ƃ��A���̐ς�
�@�@�@�@�@�@�@�@�@�@�@(d ; d')
�@�ŕ\���i�}�R�Q�Ɓj�B���̏ꍇ�A�\���̏����͐}�R�̂悤�Ɂu���|�E�v�̏��ƂȂ�B
�@�܂��A�a�͉��L�ŕ\���i�}�T�Q�Ɓj�B
�@�@�@�@�@�@�@�@�@�@�@(bj��d, d')
���̕\�L���[���ɂ��A�}�U�̃_�C�A�O�����͉��L�ŕ\�����G
�@(b0�� (f0 ; (f1 ; (b1�� f3, f4))), (f2 ; (b2�� f4, f5)))
�@�@�@�@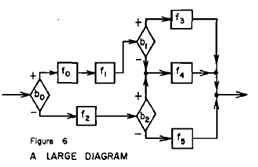
�@���̏��߂ł́A�_�C�A�O�����̑���ɘa��ς̉��Z�̓K�p���J��Ԃ����Ƃɂ��Afi��bj���琶������鎮�ɂ��ċc�_����B
�Q�D�t���[�E�_�C�A�O�����̑��̍\�z
�@�܂����߂ɁA�Q�̃_�C�A�O����d,d'�Ԃ̔������W�������̂悤�ɒ�`����G
�@�@�@�Ed'��d�̑����i���j��S�Ċ܂ނƂ��Ad�� d'�ł���Ƃ���B
�@�@�@�@�i���jd�̃G�������g�y��d���̊W
�@�܂��A�Q�̃_�C�A�O����d,d'�Ԃ� d�� d'�̊W������Ƃ��Ad��d'���ߎ�����Ƃ����B���邢�́A
d��d'�̕s���S�ȕ���(incomplete parts)�Ƃ������B
�@�ɒ[�ȏꍇ�Ƃ��āA�S�Ẵ_�C�A�O�����̋ߎ��ƂȂ�ł��e���_�C�A�O�����Ƃ��āہi�{�g���j������B�_�C�A�O�����ł́A�ہi�{�g���j�͂��̓��e������́h��h�̃{�b�N�X�ł���B���́h��h�̃{�b�N�X�͐}�V�Ɏ����悤�Ƀ_�C�A�O�����̈ꕔ�Ƃ��ĕ\������邱�Ƃ�����B�}�V�̕\���͉��L�̂悤�ɂȂ�G
�@�@�@�@�@�@�@�@(b0�� (f0 ;��), (f1 ; (b1�� f2, I )))
�@�@�@�@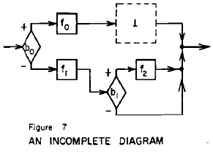
�@�@���̏��߂̖ړI�́A�h���q�h�V���{������o�����t���[�E�_�C�A�O�����𑩂̍\���Ƃ��đg�ݗ��ĂĂ������Ƃł���B�����ŁA�h���q�h�V���{���i�t���[�E�_�C�A�O�����ɂ����Ă���ȏ㕪���ł��Ȃ��V���{���j�Ƃ́A
�@�@�@�@�@��, f0, f1,�E�E�E�E, fn,�E�E�E, I,���@
�ł���A�������o���_�ɂ��āA�t���[�E�_�C�A�O�����̐ςƘa
�@�@�@�@�@�@�@�@(d ; d')�A(bj��d, d')
�y�сA
�@�@�@�@�@�@�@���_�́i��,��,���j
���g�p���đS�Ă̑g�������\�����Ă������Ƃł���B������ȉ��A����ǂ��Đ�������B
�i�P�j���q�V���{���̑�
�@���̍ŏ��̕����́A���q�V���{�� f0, f1,�E�E�E�E, fn,�E�E�E�y�� I�ɑΉ�����Bi��j�Ȃ��fi��fj�͈قȂ�̂Ō��q�V���{�� f0, f1,�E�E�E�E, fn,�E�E�E�͉��̐}�W�̂悤�ɑ��̊e�v�f�Ƃ��ĕ\������悢�B
���̑��̐}�ɂ����Ĕ������͏㏸���郉�C���ɂ��\������Ă���G
�@�@�@�@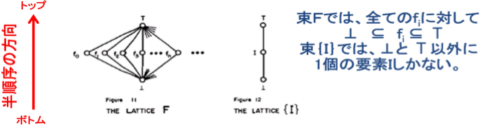
�@�@�@�@�@�@�}�W�@���q�V���{���̑�
�@���̏ꍇ�A���ア�i�������j�G�������g�͉��ŁA��苭���i�傫���j�G�������g�͏�ł���B
�i�Q�j�Q�̑��̘a
�@�f�[�^�E�t���[�̑����\�z�����ł��݂��Ɍ����Ȃ��G�������g�����Q�̑��̘a���l����B
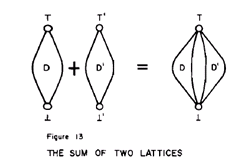
���Ȃ킿�AD, D'������,��'�������Ƃ��AD��D'���ꏏ�ɂ��ē������ꂽ��D+D'����肽���B
����́A�Q�̔������W�́h�a(union)"�ɂ��g���Ă�ꂽ�Q�̏W���̘a(union)�ɉ߂��Ȃ��B�������A���̘a�ɂ͍ő匳���ŏ������Ȃ��̂ő��ł͂Ȃ��B
�@�����ŁA�� ,��'�Ɓ�,��'���e�XD��D'�̍ő匳�ƍŏ����Ƃ���Ƃ��A�e�X�̍ő匳�ƍŏ����͓������i���Ȃ킿�A�� =��',�� =��'�j�Ƃ��邱�Ƃɂ��D+D'�͑��ƂȂ�B���̘a���`�����邱�̃v���Z�X�͐}�P�R�ɕ`����Ă���B
�@�@�@�@
�i�R�j�t���[�E�_�C�A�O�����̍ŏ��̑�
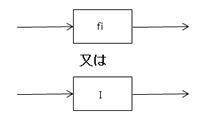
�@���q�V���{�� f0, f1,�E�E�E�E, fn,�E�E�E�y�� I�ɑΉ�����t���[�E�_�C�A�O�����̍ŏ��̑��́A���̘a���g�p����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@D0 = F + { I }
�ƕ\�������BF�̃G�������g��f0, f1,�E�E�E�E, fn,�E�E�E�ł��邪�A�e�G�������gfi��{ I }�Ɠ��^�ȑ�{ fi }�ƍl����ƁA
�@�@�@�@�@�@�@�@�@�@�@F={ f0 }+{ f1 }+�E�E�E+{ fn}�E�E�E
�@�ƕ\���ł���B�]���āAD0 = F + { I }�̃G�������g�́A���L�ƂȂ�G
�@�@�@�@
�i�S�j�_�C�A�O�����̐ςƘa
�@�@D��D'�͂��̃G�������g���h�_�C�A�O�����h��\�����Ƃ���B�_�C�A�O�����̐ς��l����Ƃ��A�ς̔������ƌĂ��D*D'��̔����������L�̂悤�ɒ�`�����G
�@�@�@�@�C�ӂ�d0, d1�� D��d'0, d'1�� D'�ɑ��āA
�@�@�@�@(d0 ; d'0)�� (d1 ; d'1)�@�́@d0�� d1����d'0�� d'1
�@�����ŁA��(d0 ; d'0)�̕\�L�ɑ���ɒ��ۓI�ɏ����t����ꂽ�g�̕\�L�Ƃ���<d0 ; d'0>���g�p����B���������āAD��D'�̐ς�
�@�@�@�@�@�@�@�@�@�@D*D'={<d ; d'> | d�� D, d'�� D' }
�@�ƂȂ�BD*D'�̍ő�ƍŏ��̃G�������g��<�� ;��'>��<�� ;��'>�B
����A�_�C�A�O�����̘a(bj��d, d')�͉��L�̑��̃G�������g�ł���G
�@�@�@�@�@�@�@�@�@B*D*D' = {<bj, d, d'> | bj��B, d��D, d'��D' }
�i�T�j�ςƘa������t���[�E�_�C�A�O�����̑�
�@���ɁAD0 = F + { I }����_�C�A�O�����̐ςƘa���g�p���Ď��̒i�K�̃_�C�A�O����D1�����L�̂悤�ɍ\������G
�@�@�@�@�@�@�@�@�@D1= D0 + (D0* D0) + (B*D0*D0)
�@����̃G�������g�͉��L�̂悤�ɂȂ�G
�@�@�@�@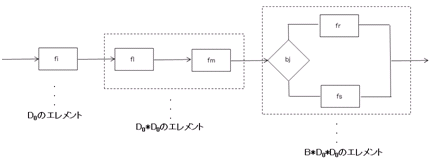
�@���炩�ɁAD1�͔��ɒZ���_�C�A�O���������G�������g�Ɋ܂�ł��Ȃ��B���傫�ȃ_�C�A�O�����邽�߂ɂ́A���̍�����i�߂Ȃ���Ȃ�Ȃ��B
����͂���ɕ��G�ȑ������L�̑Q�����ō\�����Ă����G
�@�@�@�@�@�@�@�@�@�@Dn+1= D0 + (Dn* Dn) + (B*Dn*Dn)
���̂Ƃ��A{ Dn }�͒P�������ł���B
�@��L�̂悤�ɂ��č\�����ꂽ�_�C�A�O����{ Dn }�̑S�̂́A�������W�i���j�Ɋւ��đ����\������B���̃C���[�W�����ɐ}������B
�@�@�@�@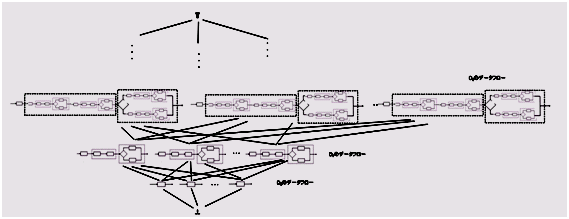
�@���̐}�́A�{�g���i�ہj����o�����ĒP���ȃ_�C�A�O�����̏W��D0����D1�AD2�ƃt���[�E�_�C�A�O�����̑��̊K�w���\�z���ꕡ�G�ȃt���[�E�_�C�A�O�������o���Ă������Ƃ�\�����Ă���B
�@�e�K�w�Ԃ̃G�������g�ɔ������̊W�i���j������B���������ƕ�����悤�ɁAD1�̃G�������g�̃l�X�g�̐[����1,�@D2�̃G�������g�̃l�X�g�̐[����2�ł���B���l�ɁA��Dn�̃G�������g�̃l�X�g�̐[���͍��Xn�ƂȂ�B
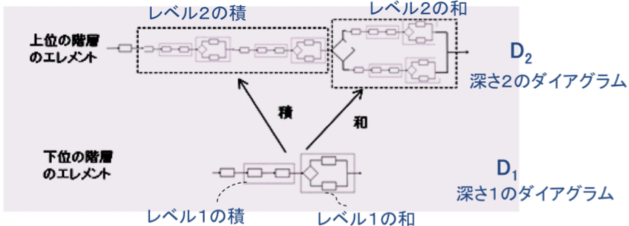
�@�����ŁA��ʂ̊K�w�̃G�������g�͂������̊K�w�̃G�������g�̐ςƘa���琶�������G�i���L�͐ςƘa�̗�j
�@�@�@�@
�����̍l�@�̌��ʂƂ��āA{ Dn }�̘a�W��
�@�@�@�@�@�@�@�@�@�@�@�@�@��Dn�@�in=0���灇�j
���l����ƁA����͑��ł��邪�������ł͂Ȃ��B���̘a�W���̃G�������g�͂Q�̃��[�h�i�ςƘa�j�ɂ�茴�q�_�C�A�O�������琶�������L���i���j�̑S�Ă̑g�����ł���B
�@�@(���j��Dn�̔C�ӂ̗v�f��d�Ƃ���ƁAd��Dn0�ƂȂ�L����n0��N�����݂���B
�@�@�@�@�@���Ȃ킿�A��Dn�v�f�͗L���̐ςƘa�̑g�����ł���B
�����ŁA�������[�v�Ȃǂ̗L���łȂ������͂ǂ̂悤�ɂ��č\������悢���A�Ƃ�����肪������B
����ɑ��ẮA���̂悤�ɗL���������������Ď������\�����ꂽ��@�̃A�i���W�[�ō\�������B
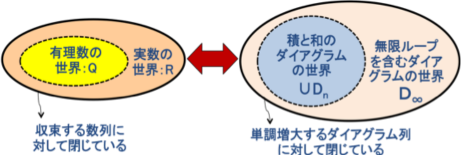
�@�L�����̐��E�FQ�@�@�@�@�@�@�@�́@�@�L���̐ςƘa�̑g��������\�������_�C�A�O�����̐��E�F��Dn
�@�@���i�R�[�V�[�j�������@�@�@ �@�@�@�@�@�@�@�@�@�@���i���́j�������@
�@�����̐��E�FR�@�@ �@�@�@�@�@�́@�@�������[�v�Ȃǂ̗L���łȂ��������܂ރ_�C�A�O�����̐��E�FD��
�@��Dn�̊��������s�Ȃ��O�ɁA�����Ƃ��Ď��Ɂu�L�����̊������v���ȒP�ɐ�������B
�R�D�L�����̊�����
�@���Ƃ��AA={x | 0��x, x2��2}�Ƃ����W�����l����B����͂��ׂĂ̗v�f���Ax��2�����̂ŗL�E�i��E�j�ł���B�������A�L�����̂Ȃ��ł́A���̏�E�͍ŏ����������Ȃ��B����A���ꂪ�����̒��łȂ�A��E�́i�Q�̕������Ƃ����j�ŏ����������A���ꂪ�W���̏���ƂȂ�B ���̈Ⴂ������(completeness)�Ƃ����B
�@������ƒ�`����Ȃ玟�̂悤�ɂȂ�B
�i�P�j�����Ƃ́H
�@�W��A�̂��ׂĂ̕����W�����A��ɗL�E�Ȃ�Ώ���������A���ɗL�E�Ȃ�Ή��������Ƃ��A�W��A�͊������邢�͏��������i���j�ł���Ƃ����B �@�i���j�������ɂ߂Ĕ������ł��悢�B
�@�i��j�����̕�� [0, 1]�́��̏����̉��Ŋ����ł��邪�A���J��� [0, 1)�͊����ł͂Ȃ��B
�@�@�@�@���R�F�P�Ɏ�������[0, 1)���̔C�ӂ̖�������������Ȃ����߁B
�i�Q�j�������Ƃ́H
�@�E�����łȂ��W���������ȏW���ɂ��邱�Ƃ��������Ƃ����B
�i�R�j�������̕��@
�@���͊������̕��@�͈�ł͂Ȃ��B�ȉ��ł͂��̈�ł���R�[�V�[��������������邪�A�f�f�L���g�̐ؒf�ɂ�銮�����Ȃǂق��ɂ��������̕��@�͂���B
�i���jAugustin Louis Cauchy(1789�N- 1857�N�j�́A�t�����X�̐��w�ҁB���ɓV���w�A���w�A���̗͊w�Ȃǂւ̍v���������B
�@�@�@�@
�i�S�j�R�[�V�[��
�@�������鐔��́A�ǂ�ǂ��k�܂��Ă��������������Ă���B�@����̓�-�_�@�Ō����ɏ������Ƃ��ł��邪�A�����ł͂�������������R�[�V�[��Ƃ������Ƃ����o���Ă����B
�@�L�������疳�����ւȂ��Ă������߂ɂ́A���������Ɋւ�鑀������Ȃ���Ȃ�Ȃ��B�Ȃ��Ȃ�A�L����̑�����s�����̂ł́A����͂܂��L�����ɂȂ��Ă��܂�����ł���B
�@�����ŁA�L�����ɑ��鑀��̌J��Ԃ��Ƃ��Đ�����l����B
�Ⴆ�A���L�̐���{an}���l����G
�@�@�@�@�@�@�@�@a1=2, an+1=(an2+2)/(2*an)�@�@�E�E�E�i�P�j
������������v�Z���Ă݂�ƁA
�@�@�@�@�@a2=(22+2)/(2*2)=6/4=3/2
�@�@�@�@�@�@a3=((3/2)2+2)/(2*(3/2))=17/12
�@�@�@�@�@�@a4=((17/12)2+2)/(2*(17/12)0=577/408
����́A�Q����n�܂��ĉ����揜�����Ōv�Z���Ă���̂ŁA�ǂ̍����L�����̂܂܂ł���B �܂��A���̐���́A�ǂ�ǂ��k�܂��Ă��������������Ă���̂ŃR�[�V�[��ƂȂ�B
���̐���͎�������l������Ƃ���A���̒l����
�@�@�@�@�@�@�@ an+1= an=���@�@�@
�����悤�Ȑ��ɂȂ�B���̏ꍇ�A��L(1)���̓�=(��2+2)/(2*��)�ƂȂ�A��2=2���烿=2�̕������i�������j�ƂȂ�B
�ȏ�̂悤�ɗL�����̗������Ƃ��A���ꂪ�R�[�V�[��ɂȂ��Ă��ċɌ��������Ă����Ƃ��Ă��A���̋Ɍ����܂��L�����͈̔͂Ɏ��܂�Ƃ͌���Ȃ��B�܂�A�����ł͂Ȃ��B
�@�����ŁA�L�����̃R�[�V�[��̋Ɍ��l��S�ėL�����ɕt��������A���̏W���̓R�[�V�[�����ɂȂ�B���ꂪ�����ł���B�i���j
�@�i���j���������Ɏ�������悤�ȈقȂ�L�������݂���̂ŁA������1��1�ɑΉ������邽�߂ɁA
�@�@�@�@�����ɂ̓R�[�V�[�̂��̂ɓ��l�W�����A����̏��W���Ƃ��Ď������`����B�j
�������āA�L���������������邱�Ƃ��ł���B��ʂɃR�[�V�[���̏W���̒��Ŏ�������悤�Ɋg�傷�邱�Ƃ��u�i�R�[�V�[�j�������v�Ƃ����B
�@�t���[�E�_�C�A�O�����̑��̊���������L�Ɠ��l�ɁA���̒P�����傷��G�������g�̃R�[�V�[��ɑ���������̂𑩂ɕt�����邱�Ƃōs�Ȃ��B
�S�D�t���[�E�_�C�A�O�����̑��̊�����
�@�ȒP�ȗ�Ń��[�v�̃_�C�A�O�������l����G
���L�̈ꎟ��������Q�����ʼn����ƁA
�@�@�@�@�@�@X��X/2 + 1�@�E�E�E�E�@�@
�܂��A�@��Q�����ŕ\������G
�@�@�@�@�@�@�@Xn+1=Xn/2 + 1�E�E�E�A�A
�A��X0=0����o�����ď����l�����߂Ă����ƁA
�@�@�@X1=X0/2+1=1�@�@�@X2=X1/2+1=1/2+1=3/2=1.5
�@�@�@X3=X2/2+1=3/4+1=7/4=1.75 X4=X3/2+1=7/8+1=15/8=1.875
�@�@�@�E�E�E���@X��=2
������t���[�E�_�C�A�O�����ŕ\������ƁA���L�̂悤�ȃ��[�v�����ɂȂ�B
�@�@�@�@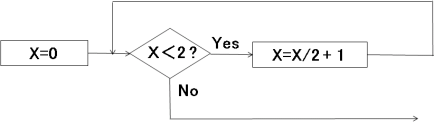
���̃��[�v������W�J���ĕ\������ƁA���L�̂悤�ɂȂ�B
�@�@�@�@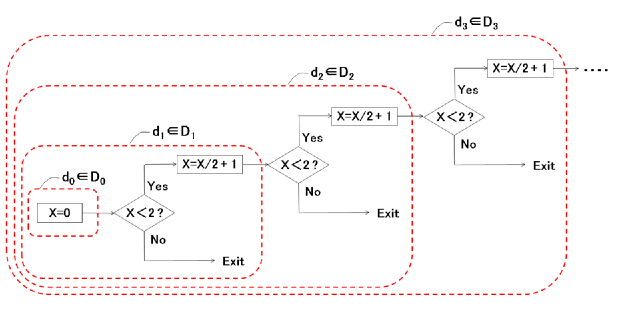
��L����A�P�����債�Ď�������_�C�A�O�����̃V�[�P���X{dn}��������G
�@�@d0��d1��d2���E�E�E��dn���E�E�E�� d
���������ď�L���[�v������ {dn}�̋Ɍ�d�ƂȂ�B
�����܂ł̋c�_����A�@
�@�@�E�L�����̃R�[�V�[��̋Ɍ��Ƃ��Ă̎����ƁA
�@�@�E�P�����傷��ςƘa�̃_�C�A�O������̋Ɍ��Ƃ��Ă̖������[�v����
�ɂ͊������Ƃ������_����ގ��������邱�Ƃ����������B
�@�@�@�@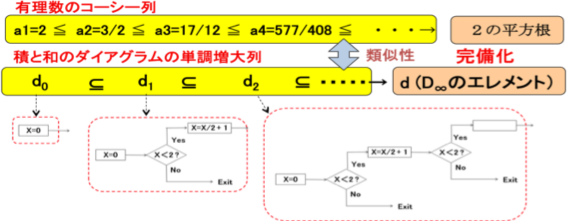
�@�ȏォ��A�ςƘa����\�������_�C�A�O�����̑���Dn�ɑ��āA��Dn�ɑ�����_�C�A�O�����̎�����{dn}�̋Ɍ���S�Ēlj����邱�Ƃɂ��A��Dn�̊�����D���������ł���B
�@����́A�L�����̃R�[�V�[��������`���邱�ƂƓ��l�Ȏ�@�ł���B
�@���Ƀt���[�E�_�C�A�O�����̊������ɂ��Č��Ă����B
�T�D�ߎ��ʑ���
�@�t���[�E�_�C�A�O�����̑��ɂ����āA�P�����傷��G�������g�̃R�[�V�[��ɑ���������̂���邽�߂ɁA�u�_�C�A�O�����̋ߎ���Ƌߎ��ʑ��Ձv���l����B
�@�E��Dn�̃G�������g�͍��Xn�́h�[���h�̃_�C�A�O�����ł���B
�@�@��萳�m�ɂ́A�����͍��Xn���x���̂Q�̃��[�h�i�ςƘa�j�̍����̃l�X�g�ɂ�萶�����邱�Ƃ���
�@�@������B�����Dn+1�̃G�������g��Dn�̃G�������g�ɂ��ߎ������Ƃ������Ƃ��������Ă���B
�@�E���AD0��D1���l����B�@D1�̗v�f��d�Ƃ���Ƃ��AD0�� D1�Ȃ̂�d��D0�܂���d��(D1- D0)�B�@
�@�@���������āA
�@�@�@(i) d��D0�Ȃ�A�����D1�̗v�fd���g�Ȃ̂Ńx�X�g�ߎ��ƂȂ�F��0 (d) = d
�@�@�@(ii) d��(D1 - D0)�Ȃ�Ad��D0�̃G�������g�ł͍����ł��Ȃ��̂ŁAd��D0�ł̋ߎ���
�@�@�@�@�@�ۂ����Ȃ��B
����������ƁAd��D1�ɑ���D0�̃G�������g�ɂ��d�̃x�X�g
�@ �ߎ���0 (d)��Ή�������ʑ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��0 : D1��D0�@
�@�@���`���邱�Ƃ��ł����G �����ŁAd��D1�ɑ��āA
�@�@�@�@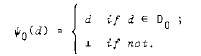
����������B
����Dn+2��Dn+1���l���A
�@ d��Dn+2�ɑ���Dn+1�̃G�������g�ɂ��d�̃x�X�g�ߎ���n+1(d)��Ή�������ʑ�
�@�@�@�@�@�@�@�@�@�@�@�@��n+1: Dn+2��Dn+1�@
���`�������B
Dn+2��Dn+1�ɂ��ẮA���L�����藧���Ƃ��v���o���ė~�����G
�@�@�@�@�@�@�@Dn+2= D0 + (Dn+1* Dn+1) + (B*Dn+1*Dn+1)
���������āA��n+1�ƃ�n�̊Ԃɂ͎��̊W����������i����͑��̍\���}����������j�G
�@�@�@�@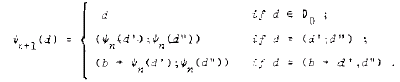
���̎ʑ���}������Ɖ��L�̂悤�ɂȂ�G
�@�@�@�@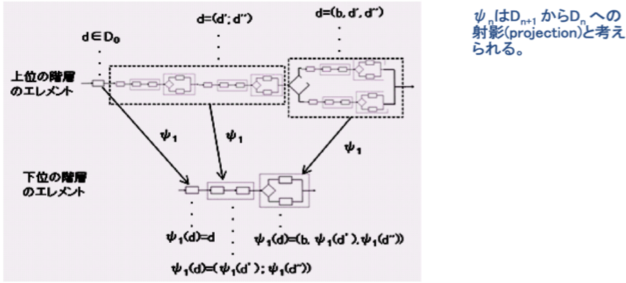
�@�ʑ���n: Dn+1��Dn�͗e�Ղɐ}���ł���B�}�P�S�ɂQ�̃_�C�A�O�������^�����Ă���F
�ŏ��̃_�C�A�O������D3�ɑ����A��Ԗڂ̃_�C�A�O�����͍ŏ��̃_�C�A�O�����Ƀ�2��K�p�������ʂł���B�}�P�S�̉��̃_�C�A�O�����ɂ͏����B���ȕ���������i�ۂ̕����j�G ���̞B�����̓_�C�A�O�����ɑ��Ď���I�Ƃ��Ɏ�菜�����B
�@�@�@�@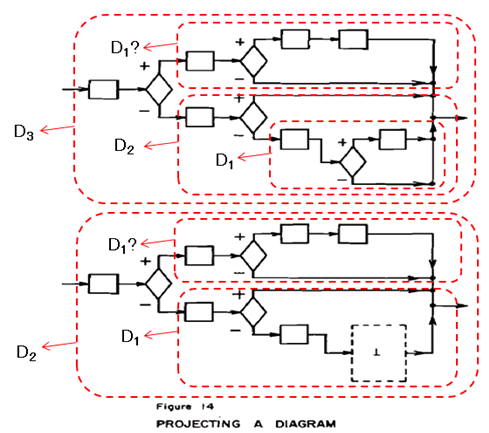
���Q�l�ɁADn+1����Dn�ւ̋ߎ��ʑ���n��L������ōl���Ă݂�G
�@�@ �@�@a1=2, an+1=(an2+2)/(2*an)�@�@������������v�Z���Ă݂�ƁA
�@�@�@�@�@a2=(22+2)/(2*2)=6/4=3/2�@�@a3=((3/2)2+2)/2*(3/2)=17/12
�@�@�@�@�@�@a4=((17/12)2+2)/2*(17/12)=577/408�@�E�E�E�E
�@�@an�ɑ��A�ʑ���n(an+1)=an�@����`�����B
�@�@�@�i��j��1(a2)=a1�̃�1(3/2)=2�@��2(a3)=a2�̃�2(17/12)=3/2
�@�@�@�@�@�@�@��3(a4)=a3�̃�3(577/408)=17/1
�U�D�L���W���ƋɌ�
�i�P�j�L���W��
�@�����W��X��D�́AX�̑S�Ă̗L�������W��X���i���Ɋւ��ājX�ɑ������������Ƃ��A�L��(directed)�ł���ƌ�����B�����C�ӂ̃y�Ax, y��X�ɓK�p����ƁAx��y��z�ƂȂ�z��X�����݂��Ȃ���Ȃ�Ȃ����Ƃ��Ӗ�����B�L���W���̖��炩�ȗ�̓֍�(��-Chain)�ł���G
�@�@�@�@�@�@�@ x0�� x1���E�E�E�E�� xn���E�E�E
���Ȃ킿�A�P�����傷���ł���B
�i�Q�j�L���W���̋Ɍ�
�@�L���W���̋Ɍ��́A��X�ł���B
�@�֍��̏ꍇ�A�Ɍ��i�����j�����L�ŕ\���G
�@�@�@�@�@�@�@�@��xn�@�in=0���灇�j�@�@
�@�@�@�@
�V�D�t���[�E�_�C�A�O�����̊�����
�@�ȏ�̏���������{ Dn }�̘a�W����Dn�in=0���灇�j���l����B
����͑��ł��邪�A��Dn�̃G�������g���琬��L���W���i���j�̋Ɍ��i�R�[�V�[��ɑ����j���l���邱�Ƃɂ��A���̊�����D�������߂�B
�@�@�i���j����̓֍��ōl���ėǂ��B
�@(A) D���� ��Dn�in=0���灇�j�̊������ł���Ɖ��肷��ƁA�u�C�ӂ�d��D���ɑ��ă�n(dn+1)=dn��
�@�@�@�������L���W���i���jd0��d1��d2�E�Edn��dn+1�E�E�����݂��Ad=��dn�in=0���灇�j�ƂȂ�B�v
�@�@�i���j����̓֍��ōl���ėǂ��B
�@(B)�t�ɁA��n(dn+1)=dn�����L���W��d0��d1��d2�E�Edn��dn+1�E�E�@(dn��Dn)�����݂���Ȃ�A
�@�@�@d=��dn�in=0���灇�j��D���̃G�������g�ƂȂ�B
�@�@�@���������āAd����Dn�̊�����D���̃G�������g�ɂȂ邱�ƂƁA�@
�@�@�@��n(dn+1)=dn�����L���W��(��) d0��d1��d2�E�Edn��dn+1�E�E�@(dn��Dn)�����݂��Ad=��dn
�@�@�@�in=0���灇�j�ƂȂ邱�Ƃ͓��l�ł���B
���Q�l�ɁAD������Dn�ւ̋ߎ��ʑ�����n�������ƗL�����̊W
�@ �ōl���Ă݂�G
�@�@�@�@a1=2, an+1=(an2+2)/(2*an)�@�@�@�@������������v�Z���Ă݂�ƁA
�@�@�@�@a2=(22+2)/(2*2)=6/4=3/2�@�@a3=((3/2)2+2)/2*(3/2)=17/12
�@�@�@�@a4=((17/12)2+2)/2*(17/12)=577/408�@
�@�@�@�@�@�E�E�E�E
�@�@�@�@�@a�� = 2�̕������i�����j
�@�@a�� �ɑ��A�ʑ�
�@�@�@�@�@�@�@�@�@����n(a��)=an�@
�@�@����`�����B���Ȃ킿�A{����n(a��)}�Ƃ����L�������琬��R�[�V�[�����G
�@�@����1(a��)������2(a��)���E�E�E�E����n(a��)���E�E�E�E�� a�� = 2�̕������i�����j
�W�D���[�v�Ƒ��̖����_�C�A�O����
�i�P�j���[�v�̃_�C�A�O������
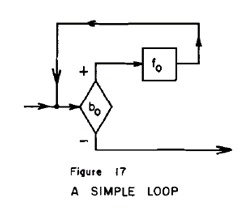
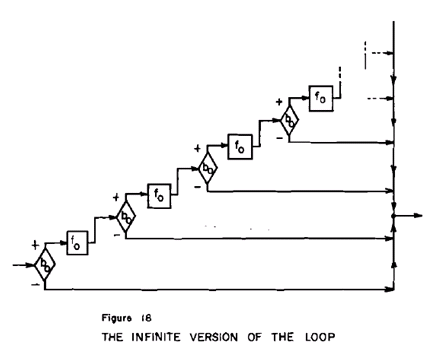
�@�@�}�P�V�͏z�̃t���[�A������while-loop�����t���[�E�_�C�A�O�����̍ł��ǂ��m��ꂽ�\���ł���B����̓v���O���~���O����@�̔��Ɋ�{�I�ȊT�O��\�����Ă���B�����I�ɁA�}�P�V�̕\�L�͍ł��P���Ȃ��̂̈�ł���B����A�}�P�W�̂悤�Ȗ����̕���̌J��Ԃ����z�̗�ł���B
�@�@�@�@
�@�@�@�@
�i�Q�j���[�v�̃_�C�A�O�����̊��\��
�@�}�P�V�̃��[�v�����́A����͂���(b0�ɂ��j���������B�@�����ŁA���������ɂ�萳�Ȃ�A����(f0�ɂ��j�ϊ�����A���[�v�ɂ��ċA�ɂ��Ăь����ɖ߂����B���������̊Ԃ͍ċA���������ƂɂȂ�B�₪�ČJ��Ԃ��ꂽ�ϊ��̗ݐό��ʂ͕��̌������ʂ���B
�@�ȏ�̂��Ƃ́A�������̃V���{�����g���ƕ�����Ղ��Ȃ�B���f�i����j�ɑ���b0,�ϊ��ɑ���f0�Ƃ����V���{�����g�p����B�ŏ��̔��f�ƕϊ��̌�A�_�C�A�O�����͂��ꎩ�g���J�Ԃ��B
���̒P���ȃp�^�[���͉��L�̂悤�ȃV���{���ŗe�Ղɕ\���ł���G
�@�@�@�@�@�@�@�@�@�@�@d = ( b0�@�� ( f0 ; d ), I )
����������ƁA��(negative)�Ŕ��f�i����j��E�o����B����A������(positive)�Ȃ�A�����菇��f0����������B���������āA�_�C�A�O�����͂��ꎩ�g���Ƃ��Ċ܂ށi�ċA�����ł���j�B
�@���̃_�C�A�O����d�͎��ۂɃt���[�E�_�C�A�O�����̊�����D���ɑ��݂��邾�낤���H������m���߂邽�߂ɁA���L�̎��ɂ���`���ꂽ����:D����D�����l����F
�@�@�@�@�@�@�@�@�@�@��(x) = ( b0�@�� ( f0; x ), I )
�@�����̓_�C�A�O�����̒P���������ł���i��1�j�B�i�^���X�L�̕s���_�藝�i��2�j���j������D�����犮����D���ւ̑S�Ă̘A�����͕s���_�����B���̃P�[�X�ł́A��X�͂������ŏ��̕s���_d��v������G�@�@�@�@�@�@�@�@�@�@�@d =��(d)
�i��1�jdn��dn+1�Ƃ���ƁA(f0�Gdn)��(f0�Gdn+1)���A��(dn) =( b0��(f0�Gdn), I)��( b0��(f0�Gdn+1), I)
�@�@�@�@�@=��(dn+1)���������āA���͒P���������ł���B
�i��2�j�s���_�藝�@�@f : D��D��������D�Œ�`����D�ɒl�����P�����Ƃ���B���̂Ƃ�F�͍ŏ��s���_p=f(p)�������Ap=��{x��D : f(x)��x}�ƂȂ�B
�X�D�܂Ƃ�
�P�D�t���[�E�_�C�A�O�����͂��̐ςƘa���瑩��Dn���\�����邱�Ƃ����������B
�Q�D�ߎ��ʑ��Ղɂ�葩��Dn�̊�����D�����\�����邱�Ƃ��ł����B
�R�D�t���[�E�_�C�A�O�����̊�����D�����x�[�X�ɂ��邱�Ƃɂ��A�i�^���X�L�̕s���_�藝��K�p���邱�ƂŁj��A�v���O�����̕s���_�̑��݂��������Ƃ��ł����B���Ȃ킿�AScott�́u�t���[�E�_�C�A�O�����̑��v�́A�v���O�����̕s���_�Ӗ��_�̓y�����Ă���B
�@�@�@�@