ƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـڈذ‰î
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‚Q‚O‚P‚S”N‚P‚OŒژپ@ڈM‰zپ@کaŒب
–عژں
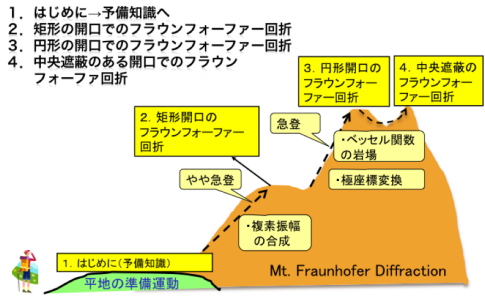
‚PپD‚ح‚¶‚ك‚ة
–{ژ‘—؟‚ً“ا‚ق‚½‚ك‚ج—\”ُ’mژ¯‚جƒyپ[ƒW‚ًچىگ¬‚µ‚ـ‚µ‚½‚ج‚إ
پuƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ‚ج‚½‚ك‚ج—\”ُ’mژ¯پv‚ًژQڈئ‰؛‚³‚¢پB
پ،ƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ‚ئ‚حپH
پ@ŒُŒ¹‚âٹد‘ھ“_‚ھƒŒƒ“ƒY‚ب‚ا‚ج‰ٌگـ•¨‘ج‚©‚çڈ[•ھ‰“‚¢ڈêچ‡‚ج‰ٌگـ‚حپuƒtƒ‰ƒEƒ“ƒzپ[ƒtƒ@پ[‰ٌگـپv
پ@‚ئŒؤ‚خ‚ê‚ؤ‚¢‚ـ‚·پBˆê•ûپAپuƒtƒŒƒlƒ‹‰ٌگـپv‚حƒtƒ‰ƒEƒ“ƒzپ[ƒtƒ@پ[‚و‚è‚à”gŒ¹‚ة‹ك‚¢ڈêچ‡‚ًˆµ‚ء‚ؤ
پ@‚¢‚ـ‚·پB
پ@“V‘ج–]‰“‹¾‚ح–³Œہ‰““_‚جگ¯‚ً‘خڈغ‚ئ‚µپAƒŒƒ“ƒY‚جƒTƒCƒY‚ة‘خ‚µ‚ؤڈإ“_‹——£‚à”ٌڈي‚ة’·‚¢‚ج‚إپA
پ@ƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ‚ھگ¬—§‚·‚éڈًŒڈ‚ً–‚½‚µ‚ؤ‚¢‚ـ‚·پB
‚QپD‹éŒ`‚جٹJŒû‚جƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ
پ،ڈَ‹µ‚جگف’è
پ@‰؛‚جگ}‚ج‚و‚¤‚ةپA‘خ•¨ƒŒƒ“ƒY‚ج‘O‚ة‹éŒ`‚جٹJŒû‚ھ’u‚©‚ê‚ؤ‚¢‚ؤ–³Œہ‰“‚جگ¯‚©‚ç‚ج”g–ت‚ح
پ@‘خ•¨ƒŒƒ“ƒY‚ة‚و‚èڈإ“_‚ةژû‘©‚·‚é‹éŒ`‚ج‹…–ت”g–تƒ°پi”¼Œa=fپj‚ة‚ب‚ء‚ؤ‚¢‚é‚ئ‚µ‚ـ‚·پB
پ@پ¨چ،Œم‚ح‚±‚جƒ°‚©‚çڈإ“_–ت‚ـ‚إ‚ً‘خڈغ‚ة‚µ‚ـ‚·پB
پ@پ@پ@پ@
پ@ژں‚ةپA‰؛‹L‚ج‚و‚¤‚ةگ¯‚©‚ç‚ج•½چs‚ب”g–ت‚ھٹJŒûپi’چپj‚ة“ü‚é‚ئ‚µ‚ـ‚·پB
پ@پi’چپj‘خ•¨ƒŒƒ“ƒY‚ھ‚ ‚éڈêچ‡‚حƒŒƒ“ƒY‚ً’ت‰ك‚µ‚½’¼Œم‚ج‹…–ت”g–ت‚ًچl‚¦‚ـ‚·پB
پ@پ@پ@پ@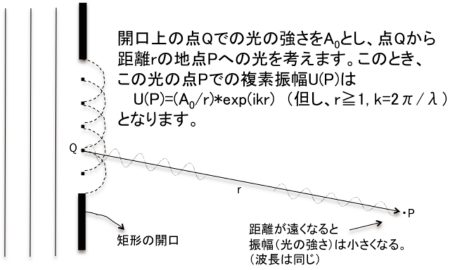
پ،‚±‚±‚©‚ç‚جکb‚جگi‚ك•û
پ@ˆب‰؛‚جژèڈ‡‚إپAٹJŒû‚©‚çڈإ“_–ت‚ج”Cˆس‚ج“_P‚ض‚ج‰ٌگـŒُ‚ھڈd‚ب‚ء‚½‚ئ‚«‚جŒُ‚ج‹‚³‚ً‹پ‚ك‚ـ‚·پG
پi‚PپjٹJŒû‚ً”÷ڈ¬—جˆو‚ة•ھٹ„‚µپA‚»‚ج—جˆو‚©‚ç“_P‚ض‚جŒُ‚ج‹‚³‚جچ‡Œv‚ً‹پ‚ك‚éپBپi‚·‚ب‚ي‚؟پA
پ@پ@”÷ڈ¬—جˆو‚©‚ç“_P‚ض‚ج•،‘fگU•‚ج‘چکa‚ً‹پ‚ك‚éپj
پi‚QپjٹJŒû‚ج‘S‚ؤ‚ج”÷ڈ¬—جˆو‚ًڈW‚ك‚ؤپAٹJŒû‘S‘ج‚©‚ç“_P‚ض‚ج‘S‚ؤ‚ج‰ٌگـŒُ‚ج‹‚³‚جچ‡Œv‚ً‹پ‚ك‚éپB
پ@پ@‚±‚ج‚ئ‚«پA•ھٹ„‚³‚ꂽ”÷ڈ¬—جˆو‚ج‘ه‚«‚³‚ًŒہ‚è‚ب‚ڈ¬‚³‚‚µپi–³Œہڈ¬پjپAٹJŒû‘S‘ج‚ة‚آ‚¢‚ؤ‚ج‘چکa‚ً
پ@پ@‹پ‚ك‚邱‚ئپA‚·‚ب‚ي‚؟’èگد•ھ‚جŒvژZ‚ًچs‚¢‚ـ‚·پB
پ@
پ@ٹJŒû‚ج•ھٹ„‚ج•û–@‚حپAٹJŒû‚ھ‹éŒ`‚جڈêچ‡‚حڈc‰،‚ة•ھٹ„‚µپA‰~Œ`‚جڈêچ‡‚ح‹ةچہ•W‚إ•ھٹ„‚µ‚ـ‚·پG
پƒ‹éŒ`‚جڈêچ‡پ„
پ@
پƒ‰~Œ`‚جڈêچ‡پ„
پ@پ@پ@
‚»‚ê‚إ‚حپAڈم‚جژèڈ‡‚ة‰ˆ‚ء‚ؤڈعچ×گà–¾‚ً‚µ‚ـ‚·پB
پ،چہ•WŒn‚جگف’è
پ@“_Q‚ح‰؛‹L‚ج‚و‚¤‚بچہ•WŒn‚جƒ°“à‚ج“_‚ئ‚µپA“_Q‚ًٹـ‚قƒ°“à‚ج”÷ڈ¬—جˆو‚ًƒ¢ƒ°=ƒ¢ƒجپ~ƒ¢ƒإ
پ@‚ئ‚µ‚ـ‚·پB‚±‚ج‚ئ‚«پAƒ¢ƒ°“à‚ج”Cˆس‚ج‘fŒ³”g‚جŒ¹‚©‚çP‚ض‚جŒُ‚حƒ¢ƒجپAƒ¢ƒإ‚ھŒُ‚ج”g’·ƒة‚و‚è
پ@ڈ\•ھڈ¬‚³‚¢‚ب‚ç‚خپA“_Q‚©‚ç“_P‚ض‚جŒُ‚ئ“¯ˆت‘ٹ(in-phase)‚ة‚ب‚è‚ـ‚·پi’چپjپB

پ@پ@پi’چپj—جˆو‚ًƒ¢ƒ°=ƒ¢ƒجپ~ƒ¢ƒإ“à‚ج”Cˆس‚ج‘fŒ³”g‚جŒ¹‚ًQپf‚ئ‚µ‚ـ‚·پB
پ@پ@پ@پ@“_Q‚©‚ç“_P‚ض‚جŒُ‚جˆت‘ٹ‚حkrپA“_Qپf‚©‚ç“_P‚ض‚جŒُ‚جˆت‘ٹ‚حkrپf‚ب‚ج‚إپA
پ@پ@پ@پ@ˆت‘ٹچ·‚حk(r-rپf)‚إ‚·پB‰؛‚جژOٹpŒ`‚©‚çپA | r– rپf|پ…(Q‚ئQپf‚ج‹——£)پ…ƒ¢ƒ°‚ج
پ@پ@پ@پ@‘خٹpگü‚ج’·‚³‚ھˆê”ت‚ةگ¬—§‚µ‚ـ‚·پB
پ@پ@
پ@پ@پ@پ@
پ@پ@پ@پ@ڈ]‚ء‚ؤپAˆت‘ٹچ·|k(r-rپf)|=(2ƒخ/ƒة)*|(r-rپf)|=2ƒخ*(|(r-rپf)|/ƒة)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ…2ƒخ*((ƒ¢ƒ°‚ج‘خٹpگü‚ج’·‚³)/ƒةپj
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@=2ƒخ*[ƒ¢ƒج2+ƒ¢ƒإ2)/ƒة]1/2پ@پEپEپE(3)
پ@پ@پ@پ@پ@‚±‚±‚إپAƒ¢ƒجپAƒ¢ƒإ‚ھŒُ‚ج”g’·ƒة‚و‚èڈ\•ھڈ¬‚³‚¢‚ج‚إ
پ@پ@پ@پ@پ@(3)ژ®پà0‚ئ‚ب‚èپAˆت‘ٹچ·|k(r-rپf)|پà0‚ھ“±‚©‚ê‚ـ‚·پB
ˆبڈم‚ج‚±‚ئ‚©‚çپAƒ¢ƒ°=ƒ¢ƒجپ~ƒ¢ƒإ“à‚ج”Cˆس‚ج‘fŒ³”g‚جŒ¹‚©‚ç“_P‚ض‚جŒُ‚حپA“_P‚إ“¯ˆت‘ٹ
‚ئ‚ب‚èپAپu”g‚جڈd‚ثچ‡‚ي‚¹‚جŒ´—پi’چپjپv‚©‚ç‚»‚جچ‡گ¬‚جŒُ‚ج‹‚³پi•،‘fگU•پj‚ًƒ¢U(P)‚ئ‚·‚é‚ئ
پ@پ@ƒ¢U(P)=ƒ¢ƒ°‚©‚ç‚جŒُ‚جگU•‚جکa=(A0/r)*exp(ikr)*ƒ¢ƒ° پEپEپEپE(4)
‚ئ‚ب‚è‚ـ‚·پi‚±‚ج‚ئ‚«‚جڈَ‹µ‚ح‰؛گ}‚ًژQڈئپjپB
پ@پi’چپj‚Q‚آ‚ج”g‚ھڈd‚ب‚èچ‡‚¤ڈٹ‚إ‚حپA”g‚جچ‡گ¬‚ح‚»‚ꂼ‚ê‚ج”g‚ة‚و‚é•دˆت‚جکa‚ة“™‚µ‚‚ب‚éپB
پ@پ@پ@پ@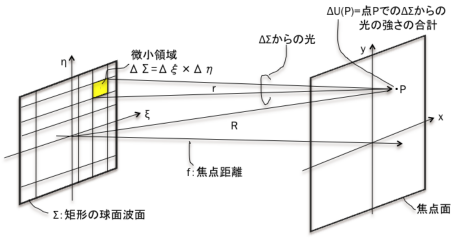
‚±‚±‚إپAƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ‚ج‘O’ٌڈًŒڈ‚إ‚ ‚éپAٹJŒû‚جƒTƒCƒY‚ئ”نٹr‚µ‚ؤڈإ“_‚ـ‚إ‚ج‹——£f
‚ھڈ\•ھ‘ه‚«‚¢ڈêچ‡پA(4)‚جگU•‚جچ€‚ج1/r‚ح1/R‚إ’uٹ·‚¦‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پi‹كژ²‹كژ—پjپB
(4)ژ®‚جگU•‚إr‚ًR‚ة’uٹ·‚¦‚é‚ئپA(A0/R)*exp(ikr)*ƒ¢ƒ°‚ئ‚ب‚è‚ـ‚·پi’چپjپB
‚±‚±‚إƒ¢ƒ°‚ًŒہ‚è‚ب‚ڈ¬‚³‚‚·‚é‚ئپA
پ@پ@پ@پ@پ@پ@پ@پ@dU(P)=(A0/R)*exp(ikr) dƒ°=(A0/R)*exp(ikr) dƒجdƒإپEپEپEپE(5)
‚ئ‚ب‚è‚ـ‚·پB
پi’چپjˆê•ûپAexp“à‚جr‚حk=2ƒخ/ƒة‚ئ‚¢‚¤‘ه‚«‚ب’lپiƒة=500nm=500*10-9m)‚ئ‚·‚é‚ئپA
پ@پ@پ@k‚ح106mˆت‚ج‘ه‚«‚ب’lپj‚ھٹ|‚¯‚ç‚ê‚ؤ‚¢‚é‚ج‚إپA’Pڈƒ‚ةrپàR‚ئ‚ح‚إ‚«‚ـ‚¹‚ٌپB
پ@پ@پ@exp“à‚جr‚ج‹كژ—‚ة‚آ‚¢‚ؤ‚حˆبچ~‚ًژQڈئپBپ@
ژں‚ةپA(5)ژ®‚جexp“à‚جr‚ًR‚ئP, Q‚جچہ•W‚إ•\‚µ‚ـ‚·پBQ‚ئP‚ج‹——£r‚حپAژO•½•û‚ج’è—‚و‚èپA
پ@پ@پ@r=[(x-ƒج)2+(y-ƒإ)2+f2]1/2پEپEپE(6)
ˆê•ûپAR=[x2+y2+f2]1/2‚و‚èf2=R2-x2-y2پ@پEپEپE(7)
پ@پ@پ@ 
(7)ژ®‚ً(6)ژ®‚ض‘م“ü‚·‚é‚ئپA
پ@r = [(x-ƒج)2+(y-ƒإ)2+R2-x2-y2]1/2=[-2xƒج+ƒج2-2yƒإ+ƒإ2+R2]1/2
پ@پ@پ@= R[1-2(xƒج+yƒإ)/R2+(ƒج2+ƒإ2)/R2]1/2
‚ئ‚ب‚èپAr‚حP‚جچہ•W(x, y)‚جٹضگ”‚ئ‚µ‚ؤ•\‚³‚ê‚ـ‚·پB
‚±‚±‚إپAٹJŒû‚جƒTƒCƒY‚ة”ن‚ׂؤR‚حڈ\•ھ‘ه‚«‚¢‚ج‚إ(ƒج2+ƒإ2)/R2‚جچ€‚ح–³ژ‹‚إ‚«‚ـ‚·پB
ڈ]‚ء‚ؤپA
پ@rپà R[1-2(xƒج+yƒإ)/R2]1/2پ@پ@پ@پ@پ@پ@
‚ـ‚½پA(xƒج+yƒإ)/R2پل1‚ب‚ج‚إ [1-2(xƒج+yƒإ)/R2]1/2پà1-(xƒج+yƒإ)/R2
‚و‚èپAr = R[1-(xƒج+yƒإ)/R2]‚ھگ¬—§‚µ‚ـ‚·پB
‚±‚ê‚ً(5)ژ®‚ض‘م“ü‚·‚é‚ئپA
پ@پ@dU(P) = (A0/R)*exp(ikr) dƒجdƒإ
پ@پ@پ@پ@پ@پ@پ@= (A0/R)*exp(ikR[1-(xƒج+yƒإ)/R2]) dƒجdƒإ
پ@پ@پ@پ@پ@پ@پ@= (A0/R)*exp(ikR)*exp(-ik(xƒج+yƒإ)/R) dƒجdƒإ
‚ئ‚ب‚è‚ـ‚·پBپ@
‚±‚±‚إ“¾‚ç‚ꂽ”÷•ھژ®پ@پ@
پ@پ@dU(P) = (A0/R)*exp(ikR)*exp(-ik(xƒج+yƒإ)/R) dƒجdƒإ
‚ً•دگ”ƒج,ƒإپi-aپ…ƒجپ…a, -bپ…ƒإپ…b)‚ة‚آ‚¢‚ؤگد•ھ‚ً‚·‚é‚ئپA
پ@U(P)=(A0/R)*exp(ikR)*پè exp(-ik(xƒج+yƒإ)/R) dƒجdƒإپ@پ@(-aپ…ƒجپ…a, -bپ…ƒإپ…b)
پ@پ@پ@=(A0/R)*exp(ikR)*پçexp(-ik(xƒج/R))dƒج*پçexp(-ik(yƒإ/R)) dƒإ
پ@پ@پ@پ@(-aپ…ƒجپ…a , -bپ…ƒإپ…b)
‚±‚±‚إپAژwگ”ٹضگ”‚جگد•ھŒِژ®پçexp(ux)dx=exp(ux)/u‚و‚è
پçexp(-ik(xƒج/R))dƒجپ@پ@(-aپ…ƒجپ…a)
پ@=[1/(-ikx/R)*exp(-ik(xa/R)]-[1/(-ikx/R)*exp(-ik(x(-a)/R)]
ƒ؟=kxa/R‚ئ’u‚‚ئپA
پ@=(-a/iƒ؟)*exp(-iƒ؟) - (-a/iƒ؟)*exp(iƒ؟)
پ@=2a*[exp(iƒ؟) - exp(-iƒ؟)]/(2iƒ؟) =2a*[(sinƒ؟)/ƒ؟]
“¯—l‚ةپAپçexp(-ik(yƒإ/R)) dƒإ=2b*[(sinƒہ)/ƒہ]پ@پ@پiƒہ=kyb/R)پ@
ڈ]‚ء‚ؤپA“_P‚إ‚جƒ°‘S‘ج‚©‚ç‚جŒُ‚جچ‡گ¬‚ج•،‘fگU•‚حپ@
پ@ U(P)=(A0/R)*exp(ikR)*2a*[(sinƒ؟)/ƒ؟]*2b*[(sinƒہ)/ƒہ]
پ@پ@پ@پ@پ@پ@پ@پ@=4ab*(A0/R)*exp(ikR)*[(sinƒ؟)/ƒ؟]*[(sinƒہ)/ƒہ]
‚ئ‚ب‚è‚ـ‚·پBپ@
“_P‚إ‚جŒُ‚ج‹“x‚ًI(P)‚ئ‚·‚é‚ئپAI(P)=U(P)‚ج“ٌڈو•½‹د
پ@=(4ab*(A0/R)*[(sinƒ؟)/ƒ؟]*[(sinƒہ)/ƒہ])2*(exp(ikR)‚ج“ٌڈو•½‹دپj‚إ‚ ‚èپA
پ@exp(ikR)‚ج“ٌڈو•½‹د=(|exp(ikR)|)2/2=1/2‚ب‚ج‚إ
پ@I(P)=(1/2)*(4ab*(A0/R))2*[(sinƒ؟)/ƒ؟]2*[(sinƒہ)/ƒہ]2پ@
پ@پi’A‚µپAƒ؟=kxa/R,ƒہ=kyb/R)
xپ¨0, yپ¨0‚ج‚ئ‚«پAƒ؟پ¨0,ƒہپ¨0‚إ‚ ‚èپA
‚±‚ج‚ئ‚«I(P)پ¨(1/2)*(4ab*(A0/R))2‚ب‚ج‚إپA
I(0)=(1/2)*(4ab*(A0/R))2‚حڈإ“_‚إ‚جŒُ‚ج‹“x‚ئ‚ب‚è‚ـ‚·پB
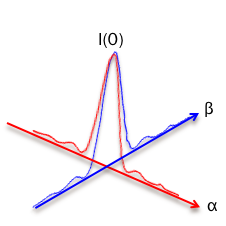
ڈ]‚ء‚ؤپAI(P)=I(0)*[(sinƒ؟)/ƒ؟]2*[(sinƒہ)/ƒہ]2پ@پEپEپEپE(6)
‚ھگ¬—§‚µ‚ـ‚·پBپ@I(P)‚ح‰؛‚ج‚و‚¤‚بƒOƒ‰ƒt‚ة‚ب‚è‚ـ‚·پB
‚RپD‰~Œ`ٹJŒû‚إ‚جƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ
‚RپD‚Pپ@‹ةچہ•W‚ج“±“ü
پ،‹ةچہ•W‚ئ‚حپH
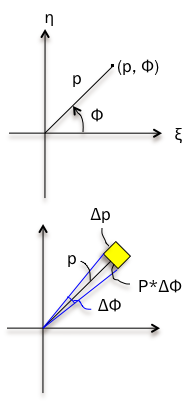
پ@•½–تڈم‚ج“_‚ًپCŒ´“_‚©‚ç‚ج‹——£p‚ئژnگüپi‰،ژ²‚جگ³‚جŒü‚«پj‚©‚ç‚ج•خٹpƒ³‚ج‘g(p,ƒ³)‚إ
پ@•\‚µ‚½‚à‚ج‚ً‹ةچہ•W‚ئ‚¢‚¢‚ـ‚·پB‚ـ‚½پAp‚ً“®Œa‚ئŒ¾‚¢‚ـ‚·پB
پ،‹ةچہ•W‚ئ’¼Œًچہ•W‚جٹضŒW
پ@’¼Œًچہ•WŒn‚ً(ƒج ,ƒإ)‚ئ‚·‚é‚ئپAƒج=p*cosƒ³ ,ƒإ=p*sinƒ³‚جٹضŒW‚ھ‚ ‚è‚ـ‚·پB
پ،‹ةچہ•W‚إ‚ج”÷ڈ¬—جˆو‚ج–تگد
پ@‰؛‚جگ}‚إپA”÷ڈ¬•خٹpƒ¢ƒ³‚ئ”÷ڈ¬“®Œaƒ¢p‚©‚çچى‚ç‚ê‚é‹éŒ`—جˆو‚جٹe•س‚ج’·‚³‚حپAƒ¢p‚ئ
پ@p*sinƒ¢ƒ³پàp*ƒ¢ƒ³‚إ‚·پBڈ]‚ء‚ؤپA‚±‚ج”÷ڈ¬‹éŒ`‚ج–تگدƒ¢W=p*ƒ¢ƒ³*ƒ¢p=p*ƒ¢p*ƒ¢ƒ³‚إ‚·پB
ƒ°‚ح”¼Œaa‚ج‰~Œ`‚ج‹…–ت”g–ت‚ئ‚µپA‹ةچہ•W(p,ƒ³)‚ً“±“ü‚µ‚ـ‚·پB‚ـ‚½پAڈإ“_–ت‚ة‹ةچہ•W(q,ƒص)‚ً“±“ü
‚µ‚ـ‚·پB‚±‚ج‚ئ‚«“_Q‚ًٹـ‚قƒ°“à‚ج”÷ڈ¬—جˆو‚ج–تگدƒ¢ƒ°=p*ƒ¢p*ƒ¢ƒ³‚ئ‚µ‚ـ‚·پB
‚ـ‚½پA‹ةچہ•W‚ئ’¼Œًچہ•W‚ج•دٹ·‚حپAƒج=p*cosƒ³,ƒإ=p*sinƒ³, x=q*cosƒص, y=q*sinƒص‚إ‚·پB

‘O‚جگك‚ج‹cک_‚و‚èپA”÷ڈ¬—جˆوdƒ°‚ة‘خ‚µ‰؛‹L‚جژ®‚ھگ¬—§‚µ‚ؤ‚¢‚ـ‚·پB
پ@U(P)=(A0/R)*exp(ikR)*پè exp(-ik(xƒج+yƒإ)/R) dƒ°
‚±‚جژ®‚إپA‹ةچہ•W‚ئ’¼Œًچہ•W‚ج•دٹ·پiƒج=p*cosƒ³,ƒإ=p*sinƒ³, x=q*cosƒص, y=q*sinƒصپj‚ًچs‚¢‚ـ‚·پG
پ@پ@xƒج+yƒإ=pq*cosƒ³cosƒص+pqsinƒ³sinƒص=pq*cos(ƒ³-ƒص)
‚ـ‚½پAƒ¢ƒ°=p*ƒ¢p*ƒ¢ƒ³‚و‚èپAdƒ°=p*dpdƒ³‚إ‚·پB
ڈ]‚ء‚ؤپA
پ@U(P)=(A0/R)*exp(ikR)*پèexp(i(-kpq/R))cos(ƒ³-ƒص))*p dpdƒ³پ@(0پ…pپ…a, 0پ…ƒ³پ…2ƒخ)
پ@‚ھ“±‚©‚ê‚ـ‚·پBU(P)‚حƒؤژ²‚ة‚آ‚¢‚ؤ‚ج‰ٌ“]‚ة‘خ‚µ‘خڈج‚ب‚ج‚إƒص=ƒخ‚ئ’u‚«‚ـ‚·پG
U(P)=(A0/R)*exp(ikR)*پèexp(i(-kpq/R))cos(ƒ³-ƒخ))*p dpdƒ³
‚±‚±‚إپAcos(ƒ³-ƒخ)=-cosƒ³‚ب‚ج‚إ
U(P)=(A0/R)*exp(ikR)*پèexp(i(kpq/R))cosƒ³)*p dpdƒ³پ@پEپEپE(7)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@(0پ…pپ…a, 0پ…ƒ³پ…2ƒخ)پ@پ@پ@
‚RپD‚Qپ@ƒxƒbƒZƒ‹ٹضگ”
(7)ژ®‚ج•دگ”ƒ³‚ةٹض‚·‚éگد•ھ‚ح
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پçexp(i(-kpq/R))cosƒ³) dƒ³پ@( 0پ…ƒ³پ…2ƒخ)
پ@‚جŒ`‚ً‚µ‚ؤ‚¢‚ـ‚·‚ھپA‚±‚ê‚حˆê”ت‚ة‚حپuƒxƒbƒZƒ‹ٹضگ”‚جگد•ھ•\ژ¦پv‚ئŒؤ‚خ‚ê‚éƒ^ƒCƒv‚جژ®‚إ‚·پB
پ،ƒxƒbƒZƒ‹ٹضگ”‚جگد•ھ•\ژ¦‚ئ‚حپH
پ@mژں‚ج‘و‚PژيƒxƒbƒZƒ‹ٹضگ”Jm(u)‚ئ‚حپA‰؛‹L‚جگد•ھژ®‚إ•\‚³‚ê‚ـ‚·پG
پ@پ@پ@پ@Jm(u)=(i-m/2ƒخ)*پçexp(i(mv+u*cosv)) dv
پ@0ژں‚جƒxƒbƒZƒ‹ٹضگ”J0(u)‚حپA
پ@پ@J0(u)=(1/2ƒخ)*پçexp(iu*cosv) dvپ@پEپEپE(8)
پ@‚ئ‚ب‚è‚ـ‚·پB
پ@mژں‚جƒxƒbƒZƒ‹ٹضگ”Jm(u)‚ئ(m-1)ژں‚جƒxƒbƒZƒ‹ٹضگ”Jm-1(u)‚جٹش‚ة‚حژں‚جٹضŒWژ®‚ھگ¬‚è—§‚؟‚ـ‚·پG
پ@پ@پ@پ@پ@پ@um*Jm(u)‚ًu‚إ”÷•ھ‚·‚é‚ئپAum*Jm-1(u)‚ئ‚ب‚éپB
پ@m=1‚ئ‚·‚ê‚خپA
پ@پ@پ@پ@u*J1(u)‚ًu‚إ”÷•ھ‚·‚é‚ئپAu*J0(u)‚ئ‚ب‚éپB
پ@‚·‚ب‚ي‚؟پA
پ@پ@پ@پ@پ@پ@پ@u*J0(u)‚ًu‚إگد•ھ‚·‚ê‚خu*J1(u)پ@پEپEپEپE(9)
پ@‚ئ‚ب‚è‚ـ‚·پB
پ@پ@
‚RپD‚Rپ@ƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ‚جژ®‚جƒxƒbƒZƒ‹ٹضگ”•\ژ¦
(7)ژ®‚ج•دگ”ƒ³‚ةٹض‚·‚éگد•ھ
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پçexp(i(kpq/R))cosƒ³) dƒ³پ@( 0پ…ƒ³پ…2ƒخ)
پ@‚ً0ژں‚جƒxƒbƒZƒ‹ٹضگ”‚إ•\ژ¦‚·‚é‚ئپA(8)‚و‚è
پ@پ@پ@پçexp(i(kpq/R))cosƒ³) dƒ³=2ƒخJ0(kpq/R)پ@( 0پ…ƒ³پ…2ƒخ)
پ@‚ئ‚ب‚é‚ج‚إپA(7)ژ®‚حپA0ژں‚جƒxƒbƒZƒ‹ٹضگ”‚إ•\ژ¦‚·‚é‚ئپA
پ@پ@پ@U(P)=(A0/R)*exp(ikR)*2ƒخپçJ0(kpq/R) *p dpپEپEپEپE(10)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@(0پ…pپ…a)
پ@‚ئ‚ب‚è‚ـ‚·پBw=kpq/R‚ئ’u‚‚ئپAp=(R/kq)*w, (R/kq)‚ح’èگ”ˆµ‚¢‚ب‚ج‚إp‚حw‚جˆêژںژ®پB
ڈ]‚ء‚ؤپAdp=(R/kq)*dw, 0پ…wپ…kaq/R‚ب‚ج‚إپA(10)‚ً•دŒ`‚·‚é‚ئپA(9)‚و‚è
پ@U(P)=(A0/R)*exp(ikR)*2ƒخ*(R/kq)2*پçJ0(w) *w dw
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@(0پ…wپ…kaq/R)
پ@=(A0/R)*exp(ikR)*2ƒخ*(R/kq)2*[J1(kaq/R) *(kaq/R)-J1(0)*0]
پ@=(A0/R)*exp(ikR)*2ƒخ*a2*(R/kaq)*J1(kaq/R)پ@
پ@=(A0/R)*exp(ikR)*2ƒخ*a2*[J1(kaq/R)/(kaq/R)]پEپEپE(11)پ@
(11)ژ® U(P)=(A0/R)*exp(ikR)*2ƒخ*a2*[J1(kaq/R)/(kaq/R)]
پ@‚©‚ç“_P‚إ‚جŒُ‚ج‹“x‚ًI(P)‚ً‹پ‚ك‚ـ‚·پB
پ@I(P)=(U(P)‚ج“ٌڈو•½‹د‚إ‚ ‚èپA(exp(ikR)‚ج“ٌڈو•½‹د=(|exp(ikR)|)2/2=1/2‚ب‚ج‚إ
پ@پ@پ@I(P)=2(A0/R)2*S2*[(J1(kaq/R) )/(kaq/R)]2پ@پEپEپE(12)
پ@پ@پ@پ@پ@پ@پi’A‚µپAS=ƒخ*a2پFٹJŒû‚ج–تگدپj
پ@qپ¨0‚ج‚ئ‚«پA(J1(kaq/R) )/(kaq/R)پ¨1/2‚ب‚ج‚إپA
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@I(0)=2(A0/R)2*S2/2
پ@ڈ]‚ء‚ؤپA(12)ژ®‚ح
پ@پ@پ@I(P)=I(0) *[2(J1(kaq/R) )/(kaq/R)]2پ@پEپEپE(13)
پ@‚ئ‚ب‚è‚ـ‚·پBƒؤژ²‚ئOwP‚جٹp“x‚ًƒئ‚ئ‚·‚é‚ئپAsinƒئ=q/R‚ب‚ج‚إ
پ@(13)ژ®‚حپA
پ@پ@پ@I(ƒئ)=I(0)*[2(J1(ka sinƒئ) )/(ka sinƒئ)]2پ@پEپEپE(14)
پ@‚ئ‚ب‚è‚ـ‚·پBپ@پ@
(13)ژ®‚إJ1(kaq/R)‚ھچإڈ‰‚ة0‚ة‚ب‚é‚ج‚حپAƒxƒbƒZƒ‹ٹضگ”•\‚©‚çkaq/R=3.83‚ج‚ئ‚«‚إ‚·پB
‚±‚ج‚ئ‚«‚جq=q0‚ھƒGƒAƒٹپ[ƒfƒBƒXƒN‚ج”¼Œa‚ئ‚ب‚è‚ـ‚·پBq0‚ً‹پ‚ك‚é‚ئپA
پ@پ@پ@q0=3.83R/ka=3.83Rƒة/ 2ƒخa=(3.83/3.14)Rƒة/2a=1.22*Rƒة/2a
ڈإ“_‹——£fپàR‚إ‚ ‚èپAŒûŒaD=2a‚ب‚ج‚إƒGƒAƒٹپ[ƒfƒBƒXƒN‚ج”¼Œaq0=1.22*fƒة/D
‚ھ‹پ‚ـ‚è‚ـ‚·پB
‚SپD’†‰›ژص•ء‚ج‚ ‚éٹJŒû‚إ‚جƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ
پ،’†‰›ژص•ء‚جˆµ‚¢
’†‰›ژص•ء‚حپA”¼Œaƒأa(0<ƒأ<1)‚ج‰~”آ‚جژص•ء‚ئ‚µ‚ؤ‚±‚ê‚ـ‚إ‚جچہ•WŒn‚ة’ا‰ء‚µ‚ـ‚·پB‚±‚ê‚ـ‚إ‚جژ®
‚ئ‚جˆل‚¢‚حپAp‚ج’l‚ج‰؛Œہ‚ھƒأa‚ئ‚ب‚ء‚½‚ج‚ف‚إ‚·پG
U(P)=(A0/R)*exp(ikR)*پèexp(i(-kpq/R))cos(ƒ³-ƒص))*p dpdƒ³
پ@پ@پ@پ@پ@پ@پ@پ@پ@(ƒأaپ…pپ…a, 0پ…ƒ³پ…2ƒخ)

پ،’†‰›ژص•ء‚ج‚ ‚éƒtƒ‰ƒEƒ“ƒtƒHپ[ƒtƒ@پ[‰ٌگـ
ڈ]‚ء‚ؤپA(10)ژ®‚حگد•ھ‚ج”حˆح‚ج‰؛Œہ‚ھ0‚©‚çƒأa‚ة•د‚邾‚¯‚إ‚·پB
پ@پ@U(P)=(A0/R)*exp(ikR)*2ƒخپçJ0(kpq/R) *p dpپ@پ@(ƒأaپ…pپ…a)
پ@پ@‚ئ‚ب‚èپAU(P)=(A0/R)*exp(ikR)*2ƒخ*(R/kq)2*پçJ0(w) *w dwپ@پ@(ƒأaپ…pپ…a)
پ@پ@=(A0/R)*exp(ikR)*2ƒخ*(R/kq)2*[J1(kaq/R) *(kaq/R) -J1(kaƒأq/R)*(kaƒأq/R)]
پ@پ@=(A0/R)*exp(ikR)*2ƒخ*a2*[(R/kaq)*J1(kaq/R) پ@–ƒأ(R/kaq)J1(kaƒأq/R)]
پ@پ@=(A0/R)*exp(ikR)*2ƒخ*a2*[J1(kaq/R)/(kaq/R)-ƒأ2J1(ƒأkaq/R)/(ƒأkaq/R)]
“_P‚إ‚جŒُ‚ج‹“x‚ًI(P)‚ئ‚·‚é‚ئپA
پ@I(P)=(A0/R)2*(2ƒخ*a2)2*[J1(kaq/R)/(kaq/R)-ƒأ2J1(ƒأkaq/R)/(ƒأkaq/R)]2پEپEپE(15)
پ@qپ¨0‚ج‚ئ‚«پAJ1(kaq/R)/(kaq/R)پ¨1/2, J1(ƒأkaq/R)/(ƒأkaq/R)پ¨1/2
‚ب‚ج‚إپAI(0)=(A0/R)2*(2ƒخ*a2)2*(1-ƒأ2)2/2پEپEپE(16)
(16)ژ®‚ً(15)ژ®‚ض‘م“ü‚·‚é‚ئپA
I(P)=[I(0)/(1-ƒأ2)2 ]*[2J1(kaq/R)/(kaq/R)-2ƒأ2J1(ƒأkaq/R)/(ƒأkaq/R)]2پEپE(17)
‚ئ‚ب‚èپA’†‰›ژص•ءپiژص•ء”ن—¦ƒأپj‚ج“_P‚إ‚ج‹“xI(P)‚ھ‹پ‚ـ‚è‚ـ‚·پB
‚±‚±‚إپA“ء‚ةƒأ=0‚ئ‚¨‚‚ئ–³ژص•ء‚جI(P)‚ة“™‚µ‚‚ب‚è‚ـ‚·پB
پ،‰ٌگـ‘œ‚ج‹“x•ھ•z‚ج”نٹr
پ@‰؛‚ج‚Q‚آ‚جƒOƒ‰ƒt‚حپi‚P‚Sپjژ®‚©‚ç‹پ‚ك‚½–³ژص•ء‚جڈêچ‡‚ئپAپi‚P‚Vپjژ®‚©‚ç‹پ‚ك‚½33%ژص•ء‚جڈêچ‡
پ@‚ج‰ٌگـ‘œ‚ج‹“x•ھ•z‚ًژ¦‚µ‚ؤ‚¢‚ـ‚·پB
پ@
پ@‚±‚ê‚ًŒ©‚é‚ئپA‰؛‹L‚ھ•ھ‚©‚è‚ـ‚·پG
پ@پ@پ@پE’†گS‚ج‹“x‚حپA’†‰›ژص•ء‚جڈêچ‡‚ح–³ژص•ء‚جڈêچ‡‚ج81%پB
پ@پ@پ@پE’†‰›ژص•ء‚جچإڈ‰‚ج‰ٌگـƒٹƒ“ƒO‚ح–³ژص•ء‚جڈêچ‡‚و‚è‚à–¾‚é‚¢پB
پ،پiژQچlپj
پ@‰ٌگـ‘œ‚ج‹“x•ھ•zƒOƒ‰ƒtچىگ¬‚ج‚½‚ك‚ةچى‚ء‚½Excel•\پiExcel‚جBESSELJٹضگ”‚ًژg—pپj
پ@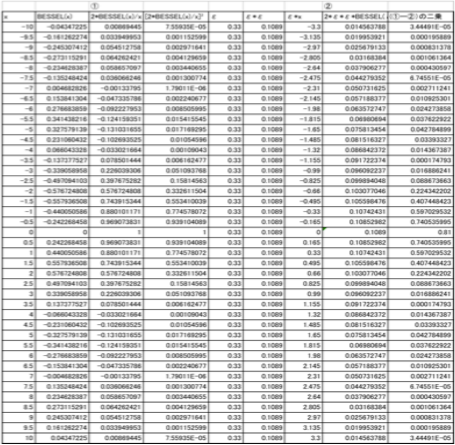
پiژQچl‚ئ‚µ‚½ڈ‘گذپj
پ@…@Hecht’ک Optics Third Edition, Addison Wesley, 1998‚ج‘و‚P‚Oڈح Diffraction
پ@…ADaniel J. Schroeder’کپ@Astronomical Optics, Second Edition, Academic Press, 2000
پ@پ@‚ج‘و‚P‚OڈحDiffraction Theory and Aberrations