�@�K���A�ڑ��̗R��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2013�N �쐬�@�M�z�@�a��
�@�K���A�ڑ�(Galois connection)�̘b��ɓ���݂̂Ȃ��l�́A���̂��Ƃ�m�肽���Ǝv����������Ȃ��G
�@�@�E���̋N���͉����H
�@�@�E����͂ǂ��Ŏg���Ă��邩�H
�@�@�E���̗��_�̎�v�ȊJ��҂͂��ꂩ�H
�P�D�P�@�K���A�ڑ��̗��j
�@�ȒP�ɗ��j��U��Ԃ�A
�@�E19���I�̒i�K�ł́A���O�����W���A�A�[�x���A�K���A�A�f�f�L���g�̂悤�ȃK���A���_�̊J��҂���
�@�@�̌����ɑ�������@��������Ƃ͂ł��邯��ǂ��A�i����Ō����j�K���A���_�̊T�O�͂܂�����
�@�@��Ă��Ȃ������B
�@�E20���I�ɂȂ�ABirkhoff��"polarities(�ɐ�)"�AOre��"Galois connexions"�A������"Adjunctions
�@�@(����)"�Ƃ��Ēm���Ă���Schmidt��"Galois correspondences of mixed type"�́A�K���A�ڑ���
�@�@����I�Ȍ����ւ̃}�C���X�g�[���ƂȂ����B
�@
�P�D�Q�@�K���A�ڑ��̒����I����
�@�K���A�ڑ��́A���L�̂悤�ɂQ�̐��E���֘A�t������̂ł���B
"In their most general sense, adjunctions and /or Galois connections make it possible to relate two "worlds" of (more or less mathematical) objects with each other in order to gain information about one world by passing to the other, perhaps better known world."(��ʓI�ȈӖ��Ő����܂��̓K���A�ڑ��́A����̐��E�ɂ��Ă̏����悭�m��ꂽ���E�ł��鑼���ɓn�����Ƃœ��邽�߂ɁA��{�I�ɂ͐��w�I�ΏۂƂ����Q�́h���E�h�����݂��ɊW�t���邱�Ƃ��ł���B)
�@���̍l���̋N����E.�K���A�i���j�ɂ���̂�20���I�ɂȂ��ăK���A�ڑ��ƌĂ��悤�ɂȂ����B
�@�@(��)19���I�t�����X�̐��w�� E.�K���A(1811�`1832)�Ɉ��ށB�G�R�[���E�m���}���݊w���ɑ㐔�w
�@�@�@�@�ɂ�����K���A���_���m�������i20�̂Ƃ������Ŏ����j�B
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@ (Je n'ai pas le temps�F���Ԃ��Ȃ��j
�@�ȒP�Ɍ����A�Q�̓T�^�I�ȁh���F���I���E�h�͓����܂��͕s�����̍��ӑ��ƉE�ӑ��ɂȂ邱�Ƃ��ł���B
���̂悤�ȏ̋L�q�́i�[�j�����W���Ԃɒ�`���ꂽ����
�@�@�@�@�@�@�@�@�@��(p)��q��p����(q)
�@�@�@�@�@�@�@�@�@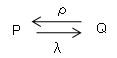
�@�����肵���ʑ��̑ɂ��s�Ȃ���B
�@�i���j�������F���˗��Ɛ��ڗ��݂̂����ꍇ���[����(quasi-order)�Ƃ����B
�@�@�@�@�{�����̐����ł́A�����ɁA�����ςɑΉ��B
�����ŁA�����ɂ��Đ�������G
�@�����W���Ԃ̎ʑ��ɁFP��Q����уρFQ��P���C�ӂ�p��P�Aq��Q�ɑ���
�@�@�@�@�@�@�@��(p)��q�@�́@p����(q)�@�@
�@�����Ƃ��A�ʑ��i�ɁA�ρj�͐����ł���Ƃ����B�܂��A�ɂ��ς̍������A�ς��ɂ̉E�����Ƃ����B
�@�������̐�����
�@�E��(�ρi�Ɂj�j=�Ɂ@�@�@�E�ρi�Ɂi�ρj�j=�ρ@�����藧�B
���K���A�ڑ��Ƃ͉����H�@
�@�ʏ�A�K���A�ڑ��Ƃ����p��́A����(adjunctons)�ƌĂԂ��̂̓��`��Ƃ��Ďg�p�����B�{�����ł����̈Ӗ��Ŏg�p���Ă���B�������A�����ɂ́A������"����(covariant)"�ƃK���A�ڑ���"����(contravariant)"�͖{���͋�ʂ���Ă����B
�@�@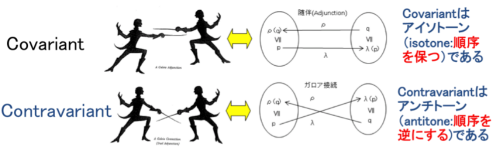
�@���̂悤�ɁA2�Ԗڂ̏����W��Q�̏������t�](inverted)���邱�Ƃɂ��A���l�̒�`���h�V�����g���b�N�h�ƂȂ�K���A�ڑ��̌ÓT�I��`�ɓ��B����F�@p����(q)�@�� q����(p)
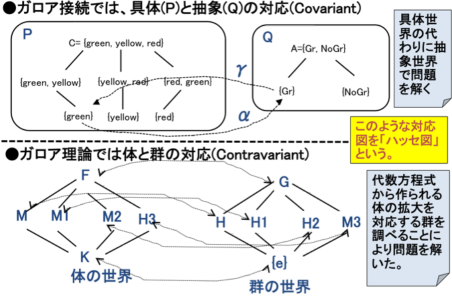
�@�Q�l�ɁA�K���A�ڑ��ƃK���A���_�̃K���A�Ή����r����Ǝ��̂悤�ɂȂ�B
�@�@�@
�i�Q�l�j�`���T�O����(Formal Concept Analysis)
�@�K���A�ڑ��̐��w�ȊO�̓K�p��Ƃ��Č`���T�O���͂�����B
�@�@���̐V�������H�w���̐��w�I�Ɋ�b�t����ꂽ���_��Rudolf Wille�Ƃ��̋��������҂ɂ��1970
�@�@�N��Ɏn�܂�L�߂�ꂽ�B
�@�A�`���T�O���͂́A�ɐ��Ƒ��_�Ƃ������w�I�T�O�𐔊w�����łȂ��N�w�I�T�O�╪�ގ�@�A�H�w�A
�@�@�����w�A��w�A���j������p�A���y�܂ŗl�X�Ȑ��w�O�̗̈�Ɍ��ѕt����B
�@�B���̃e�[�}�ɂ��Ă̕�����Ղ����͉��L�̖{���Q�ƁG
�@�@�@Ganter, B Wille, R. : Formal Concept Analyaia - Mathematical Foundation. Springer, 1999