widening����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2013�N12���@�@�M�z�@�a��
�@���̎����́A���߂�widening�̗v�_��������A���̌�ɎQ�l�Ƃ���Flemming Nielson�����FPrinciples of Program Analysis�̑�4�́@Abstract Interpretation��widening�̓��e���Љ��B
�P�Dwidening�̗v�_
�@���ۉ��߂ł́A�v���O�����̈��S���i�Ⴆ�Εϐ����I�[�o�[�t���[���Ȃ��Ȃǁj�̓v���O�����̃Z�}���e�B�N�X���l���A�ϐ��̒P�����傷�鑶�ݔ͈͂̍ŏ��s���_�����߂邱�Ƃœ�����B���̂Ƃ��ŏ��s���_�����݂��邱�Ƃ̓^���X�L�̕s���_�藝����ۏ���邪�A����͑��ݒ藝�ł���A���ۂɂ͂��̕s���_�̋ߎ��l��L����̑���ŋ��߂���@���K�v�ƂȂ�Bwidening�͂�������߂��@�ł���B
�P�D�P�@widening���Z�q�̒�`
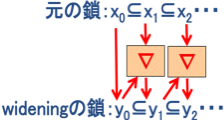
�@���L�����Ƃ��A�ށFL�~L��L��widening���Z�q�ł���Ƃ����G
�@�@�@�@ �ނ͏�E���Z�q�ł���B���Ȃ킿�A�C�ӂ�x, y��L�ɑ��āAx��y��x��y
�@�@�@�A �L����(Chain)�̏����F�@�C�ӂ̒P�����傷�鍽 x0��x1���E�E�E��xn�E�E�E�ɑ��āA
�@�@�@�@�@�މ��Z�q�ɂ�鍽�@y0=x0, y1=y0��x1, y2=y1��x2,�E�E�E, yn+1=yn��xn+1,�E�E�E
�@�@�@�@�@�@�́A�L���ň��肷��i���傪�L����Ŏ~�܂�j
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�i��jwidening���Z�q�̋�̗�Ƃ��Ă͉��L������G
�@�@�@�@�@�@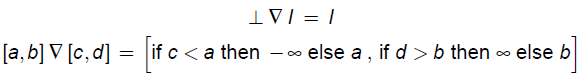
�P�D�Q�@widening���Z�q�̐���
�@����widening���Z�q�ނ���`�ł����Ƃ��A������L��ɗ^����ꂽ�C�ӂ̒P�����i���jf�FL��L���^����ꂽ�Ƃ���B�@
�@�@�i���j�������W��L���f�FL��L���P����(monotone function)�ł���Ƃ́A�C�ӂ�l, l'��L��
�@�@�@�@���āAl��l'�Ȃ��f(l)��f(l')���������邱�ƁB���Ȃ킿�A�����ۑ��ł���Bisotone�Ƃ������B
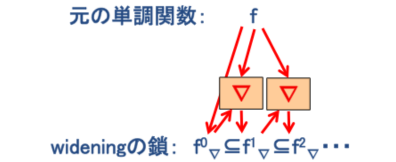
���̂Ƃ��Af��widening���Z�q�ނ��牺�L�̎�
�@�@�@�@�@�@�@�@�@�@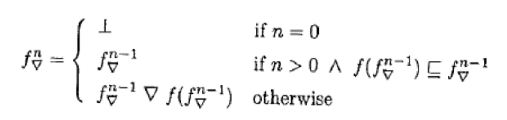
�ɂ�萶�������㏸��(fn��)n�Ff0��=��, f1��=�ہ�f(��), f2��= f1����f(f1��),�E�E�E�͗L����ő������~�߂Ĉ��肵�A����f�̍ŏ��s���_�̋ߎ��ƂȂ邱�Ƃ��������i���̏ؖ��͎��ňȍ~���Q�Ɓj�B�܂�Awidening���Z�q��f�̕s���_�̋ߎ��l��L����̑���ŋ��߂���@����Ă���B
�@�@
�ȏ��Z�߂�ƁA
�@�uwidening���Z�q�ނ���`���ꂽ�Ƃ���ƁA��������̒P����f�̍ŏ��s���_�̋ߎ��́Af�ɂ��́ނ�L�����p�����邱�Ƃœ�����B�v
�@widening�̋�̗�G
��Ԃ̏W���ɑ���widening���Z�q���ȉ��̂悤�ɒ�`����
�@�@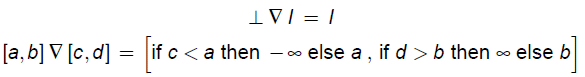
���̂Ƃ��A�ނ�widening���Z�q�̏��������G
�@(xn)�F�ہ�[0, 0]��[0, 1]��[0, 2]���E�E�E�E
�@�ɑ��āAy0=��, y1=y0��x1=�ہ�[0, 0]=[0, 0], y2=y1��x2=[0, 0]��[0, 1]=[0,��],
�@�@�@�@�@�@�@�@�@y3=y2��x3=[0,��]��[0, 2]=[0,��]
�@�ƂȂ�A(yn)�F�ہ�[0, 0]��[0,��]=[0,��]�E�E�E
�@���Ȃ킿�A�L����i3��j��[0,��]�Ɏ�������B
�A���L�̍ċA�����̎���widening�ʼn����G
�@�@�@�@�@�@�@
��L�̎��͍����̕ϐ�X2���E���̕ϐ�X2�̊��ŕ\������Ă���i���Ȃ킿�A�E���̕ϐ�X2�ɑ��ĉE���̎��̒l���ϐ�X2�̎��̒l�����߂�j�B�������F�ŕ\������ƁA
�@�@�@�@�@�@�@�@�@X2(i+1)=F(X2(i))=[0, 0]��((X2(i)��[-��, 99])[x:=x+1])
���̎��̕ϐ�X2�̍ŏ���4�̒l�iX2(0),X2(1),X2(2),X2(3))�����߂�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@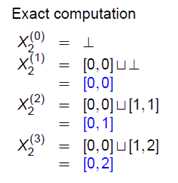
���������āAF�͉��L��Ή�������P�����ł���G
�@�@�@�@F(��)=[0, 0], F([0, 0])=[0, 1], F([0, 1])=[0, 2], ...F([0,��])=[0,��]
��L��F0(��)=�ۂƂ��Ď��̂悤�ɕ\���ł���G
�@�@�@�@F1(��)=[0, 0],
�@�@�@�@F2(��)=F(F1(��))=F([0, 0])=[0, 1],
�@�@�@�@F3(��)=F(F2(��))=F([0, 1])=[0, 2],
�@�@�@�@�@...
���Ȃ킿�AF0��F1��F2��F3���E�E�E
�@���̒P����F�ɑ��A��Ԃ̏W���Œ�`����widening�ނ���P�D�Q����fn���̂悤�ɏ㏸��������Fn���͗L����ň��肷��G���ہA
�@�@�@�@�@�@�@�@F0��=��,
�@�@�@�@�@�@�@ F1��= F0����F(F0��)=�ہ�F(��)=�ہ�[0, 0]=[0, 0]
�@�@�@�@�@�@�@�@�@F2��= F1����F(F1��)=[0, 0]��F([0, 0])=[0, 0]��[0, 1]=[0,��]
�@�@�@�@�@�@�@�@�@F3��= F2����F(F2��)=[0,��]��F([0,��])=[0,��]��[0,��]=[0,��]
���Ȃ킿�Awidening���Z�q�ɂ��
�@�@�@�@�@�@�@F0��F1��F2��F3���E�E�E�Ƃ����L���łȂ��P��������ɑ��A
�@�@�@�@�@�@�@F0����F1����F2��= F3��=�E�E�E�Ƃ����L���ň��肷��P�����������B
�����ŁAF0����F1����F2��= F3��=�E�E�E�̈��肵���lF3����X=F(X)�ɑ�����邱�Ƃ��l����G
����͏k���ʑ�F(Fm��)�� Fm���ƂȂ�AF(Fm��)��F�̍ŏ��s���_�̋ߎ��l�ƂȂ邱�Ƃ��m���Ă���i���̏ؖ��͑�Q�ߎQ�Ɓj�B
��L�̗��F(F2��)�����߂�ƁA
�@�@�@�@�@�@F(F2��) =[0, 0]��((F2����[-��, 99])[x:=x+1])
�@�@�@�@�@�@�@�@�@�@�@�@�@=[0, 0]��(([0,��]��[-��, 99])[x:=x+1])
�@�@�@�@�@�@�@�@�@�@�@�@�@=[0, 0]��(([0, 99])[x:=x+1])
�@�@�@�@�@�@�@�@�@�@�@�@�@=[0, 0]��[0, 100]
�@�@�@�@�@�@�@�@�@�@�@�@�@=[0, 100]
�����}�Ŏ����Ǝ��̂悤�ɂȂ�G
�@�@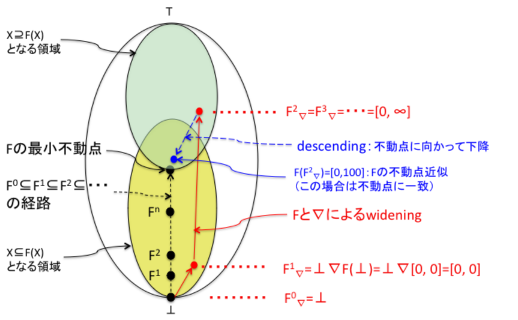
�@�y��}�̐����z�@F�̍ŏ��s���_�̋ߎ���L����̑���ŋ��߂邽�߂ɁAF0��F1��F2��F3���E�E�E�Ƃ����L���łȂ��P��������̑���ɁAF0����F1����F2��= F3��=�E�E�E�Ƃ����L���ň��肷��P������������A�����F(X)�ɑ���iF(F2��))���Ă���B
��Cousot��MIT�u�`������widening�}���ɂ���
Cousot��MIT�u�`�̃X���C�h1�ł�widening�����L�̎菇�i�@�`�B�j�ŕ\�����Ă���G
�@�܂��A��Ԃ̊�������̒P����F�����L�Œ�`����G
�@�@�@�@�@�@�@�@�@�@�@F(��Ԃ̃g���[�X�j=�g���[�X�̊e��Ԃ̘a
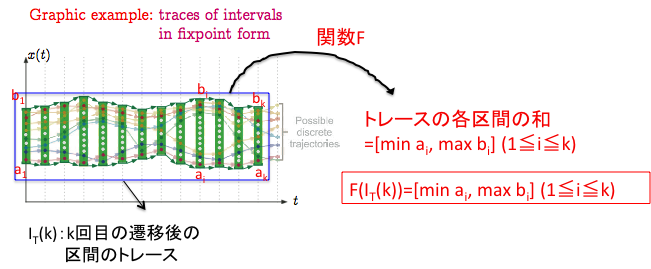
�@�@���̂Ƃ��AF�͒P���������ɂȂ�G
�@�@
�A��Ԃ�widening�ނ̒�`�͉��L���g�p����G
�@�@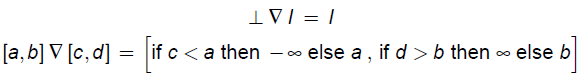
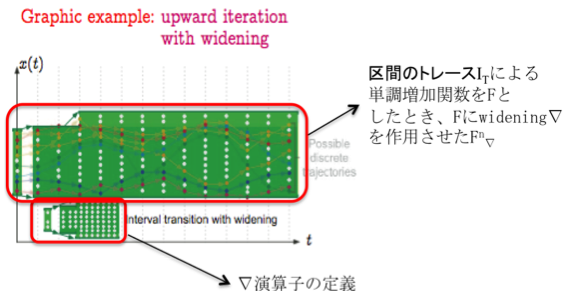
�B��Ԃ�widening�ނ����肷��}�����ɁA�ނ���F�ɍ�p������Fn�������肷��}����ł���G
�@�@�@�@�@�@
�Q�D�i�Q�l�jPrinciples of Program Analysis�̑�4�͂�widening�Љ�
�@���̖{�ɂ́A�uwidening���Z�q�ނ���`���ꂽ�Ƃ���ƁA��������̒P����f�̍ŏ��s���_�̋ߎ��́Af�ɂ��́ނ�L�����p�����邱�Ƃœ�����B�v���Ƃ̐��w�I�ؖ���������Ă���̂ŁA���L�ɂ�����Љ��B�ؖ��͏������������w�I�A�[�@�Ɣw���@���g�p���Ă���B
�Q�D�P�@�p��̐���
�@�v���O�����̃Z�}���e�B�N�X
�@�v���O����p�̃Z�}���e�B�N�X�́A��ԁA��ԁA�{���x�̎����̂悤�Ȓl�̏W��V�ɑ��A�v���O����p��V�̂P�̒lv 1�𑼂̒lv2�ɂǂ̂悤�ɕϊ����邩���K�肷��B
�@�@�i��j�g���[�X�Z�}���e�B�N�X�F�v���O�����|�C���gpp�ƕϐ��̒lx�̑g(pp, x)�̏W���B
�@�@�@�@�@�������(pp, x)���ǂ̂悤�ɐ��ڂ��邩�������Ă���B
�A�v���O�������
�@�v���O������͂Ƃ́A���ۋ�ԁA�����̏㉺���̂悤�ȃv���p�e�B�̏W��L�ɑ��A�v���O���� p��L�̂P�̃v���p�e�Bl1�𑼂̃v���p�e�Bl2�ɂǂ̂悤�ɕϊ����邩���K�肷��B
���Ȃ킿�A�v���O����p�̃v���O������͂�fp�Ƃ���ƁAfp(l1)= l2�ł���B�����ŁAf���P���ł���Ƃ����v���̓v���O���N��͂Ŕ��Ɏ��R�Ȃ��Ƃł���B
�Q�D�Q�@�L���ȗ�ŕs���_�ߎ������߂邱��
�@������L=(L,��,��,��,��,���j��^�����Ƃ��A�P�̃v���p�e�Bl1�𑼂̃v���p�e�Bl2�ɕϊ�����v���O ����p�̌��ʂ̓v���O����p�Ɉˑ�����P����fp�F L�� L�ɑ��Ď�fp(l1)=l2�ɂ��^������Bfp���P���ł���Ƃ����v���̓v���O���N��͂Ŕ��Ɏ��R�Ȃ��Ƃł���G ����͒P�ɁAl1'��l1��菬�����l���L�q����Ȃ�Afp(l1')��fp(l1)��菬�����l���L�q���邱�Ƃ������Ă��邾���ł���B
�@�ċA�I�܂��͌J��Ԃ��̃v���O�����̍\���ɑ��ẮA�L���̌J��Ԃ��v���Z�X�̌��ʂƂ��āA�ŏ��s
���_(least fixed point) lfp(f)���l���������B�������L���͈̔͂ł́A�P����������J��Ԃ��̃V�[�P���X (f n(��)) n =( f (��),f2(��)=f (f (��)), f3(��)=f (f (f (��))),�E�E�E, fn(��)=f (�E�E�Ef (f (��))) )�͍ŏI�I�Ɉ��肷��K�v�͂Ȃ��A���̏���͕K������lfp(f)�Ɠ������Ȃ�K�v�͂Ȃ��B
�@�L���̌J��Ԃ��̃V�[�P���X(f n(��)) n�͍ŏI�I�Ɉ��肷�邱�Ƃ����̏�����K��lfp(f)�Ɠ������Ȃ�Ƃ������Ƃ��ۏł��Ȃ��̂ŁAlfp(f)���ߎ����鑼�̕��@���l���Ȃ���Ȃ�Ȃ��B
�������ɁAwidening�Ƃ����T�O���o�ꂷ��B���̊T�O�́A�ŏI�I�Ɉ��肵�ŏ��s���_�̈��S�ȁi��ʁj�ߎ��̒l�������ƂŒm����V�����V�[�P���X(f��n ) n�ɂ��(f n(��)) n��u�����邱�Ƃł���B
�Q�D�R�@��E���Z�q(upper bound operators)
�@������L=(L,�� )��̉��Z�q���`�FL�~L�� L�͉��L�����藧�Ƃ��A��E���Z�q�ƌĂ��G
�@�@�@�@�C�ӂ�l1, l2��L�ɑ��āAl1�� ( l1���`l2)�� l2
���Ȃ킿�A���Z�q���` �͏�ɂ��̈����̂ǂ�������傫�ȗv�f��Ԃ��B
(ln)n={l1, l2,�E�E�E, ln}��L�̗v�f�̃V�[�P���X�Ƃ��A�ӁFL�~L��L��L��̑S���(total function)�Ƃ���B�ӂ��g�p���Ĉȉ��Œ�`�����V�����V�[�P���X(l��n)n={l��1, l��2,�E�E�E, l��n}���\������i�j�G
�@�@�@�@�@�@�@n=0�̂Ƃ��Al��n= ln�@�@n���O�̂Ƃ��Al��n= l��n-1��ln�@�@�@�@�@�@�@�@�@�@�i���P�j
�@�@�@�i�j ��������W�J����ƁAl��n�̓ӂɂ��l0����ln�܂ł̍������ŕ\�����G
�@�@�@�@�@�@�@�@�@�@�@l��0=l0
�@�@�@�@�@�@�@�@�@�@�@l��1=l��0��l1=l0�ӂ��P
�@�@�@�@�@�@�@�@�@�@�@l��2=l��1��l2=(l0�ӂ��P)��l2
�@�@�@�@�@�@�@�@�@�@�@l��3=l��2��l3=((l0�ӂ��P)��l2)��l3
�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E
�@�@�@�@�@�@�@�@�@�@�@l��n=l��n-1��ln=((l0�ӂ��P)��l2)��l3)�ӁE�E�E)��ln
���̂Ƃ��A�C�ӂ̃V�[�P���X�͎���Fact 4.11�̂悤�ɏ�E���Z�q�ɂ��㏸���ɓ]�����邱�Ƃ��ł���F
Fact�S�D�P�P �@(ln)n���V�[�P���X�Ƃ��A���`����E���Z�q�Ƃ���Ƃ��A(l���`n)n�͏㏸���ł���G ����ɁA
�S�Ă�n�ɑ��āAl���`n �� ��{l0, l1, ..., ln}
�ؖ��@(l���`n)n���㏸���ł��邱�Ƃ������ɂ́A�C�ӂ�n�ɑ���l���`n�� l���`n+1�������悢�B
n=0�Ƃ���ƁA��L�́i���P�j�Ń�=���`�ƒu���A���`����E���Z�q�ł��邱�Ƃ���l���`0= l0��l0���`l1= l���`1
���������āAn=0�̂Ƃ� (l���`n)n�͏㏸���ł���Bn��0�̂Ƃ����`����E���Z�q�ł��邱�Ƃ���l���`n ��
l���`n���`ln+1�ƂȂ�B����A��L�́i���P�j����n��0�̂Ƃ�l���`n ���`ln+1 = l���`n+1�ł���B���������āAn��0�̂Ƃ��Al���`n��l���`n+1���������A�㏸���ƂȂ�B �܂��Al���`n-1 ���`ln = l���`n�����`����E���Z�q�ł��邱�Ƃ���ln��(l���`n-1 ���`ln )= l���`n�ƂȂ�Aln��l���`n����������B���������āAl0��l���`0, l1��l���`1, l2��l���`2,�E�E�E, ln��l���`n����(l���`n)n���㏸���ł��邱�Ƃ���l0, l1, ..., ln��l���`n ��������B�@��
�Q�D�S�@widening���Z�q(widening operators)
�@�ŏ��s���_�̋ߎ��Ɏg�p�ł�����ʂȃN���X�̏�E���Z�q�ނ�����B
���Z�q�ށFL�~L��L�͉��L�̏��������Ƃ�widenig���Z�q�Ƃ����G
�@�� �ނ͏�E���Z�q�ł���B
�@�� �C�ӂ̏㏸��(ln)n�ɑ��āA�㏸��(ln��)n�͍ŏI�I�Ɉ��肷��B
�@
(ln��)n�����ۂɏ㏸���ł��邱�Ƃ�Fact4.11���瓱�����B
�ނ��ŏ��s���_�̋ߎ����T�|�[�g����Ƃ����l���͈ȉ��̒ʂ�ł���G
�P����f�FL��L����������ɗ^�����Awidening���Z�q�ނ��^����ꂽ�Ƃ��A���L�̎��ɂ���`�� �ꂽ�V�[�P���X(fn��)n���v�Z����B
�@�@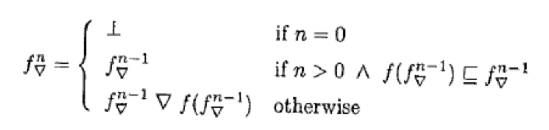
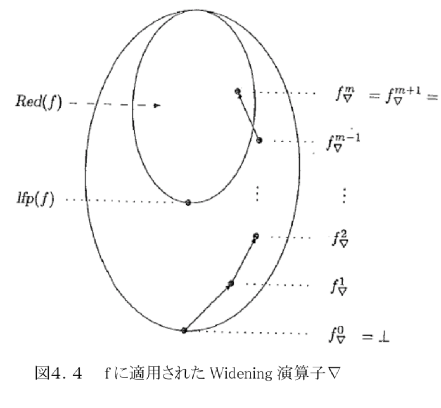
Fact�S�D�P�P�ɂ��A����͏㏸���ł��邱�Ƃ�������i���̏ؖ���Fact4.14��(i)���Q�Ɓj�A���̖���4.13�ɂ�肱�̃V�[�P���X���ŏI�I�Ɉ��肷�邱�Ƃ�ۏ���BFact�S�D�P�S����A����͂���m�ɑ���f(fm��)��fm���ł��邱�Ƃ��Ӗ�����B�����f��fm���ŏk���I(reductive)�ł��邱�Ƃ��Ӗ����A�^���X�L�̕s���_�藝����f m����lfp(f)�łȂ���Ȃ�Ȃ����Ƃ�������i���̏ؖ���Fact4.14��(iv)���Q�Ɓj�G���������āAlfp(f)�̖]�܂������S�ȋߎ��Ƃ��āA lfp��(f) = fm�� ��������B�}�S�D�S�ɂ��ꂪ�}������Ă���B
�������Af(fm��)��fm���ł���Af(fm��)��lfp(f)�Ȃ̂ŁA���̋ߎ�lfp��(f)��f(fm��)�ɂ����P�����Bf���J��Ԃ���
f(fm��)��f2(fm��)���E�E�E��fn(fm��)��lfp(f)�Ƃ������~��(descending chain)�������A�ߎ�lfp��(f)��fn(fm��)�ɂ�肳��ɉ��P�����B
�@�@�@�@�@�@�@�@�@�@�@�@�@
---------------------------------------------------------------------
���� �S�D�P�R�@�ނ�widening���Z�q�Ȃ�A�㏸��(fn��)n�͍ŏI�I�Ɉ��肷��B
---------------------------------------------------------------------
����S�D�P�R�̏ؖ��̏����Ƃ��āA�ȉ���Fact���ŏ��Ɏ����G
Fact�S�D�P�S�@�ނ�widening���Z�q�Ȃ�A���L����������G
(i)�V�[�P���X(fn��)n�͏㏸���ł���B
(ii)����m�ɑ���f(fm��)��fm���Ȃ�A�C�ӂ�n��m�ɑ���(fn��)n�͍ŏI�I�Ɉ��肷��F
�@���Ȃ킿�Afn��= fm�� ����nfn��= fm��
(iii) (fn��)n���ŏI�I�Ɉ��肷��Ȃ�Af(fm��)��fm���ƂȂ�悤��m�����݂���B
(iv) (fn��)n���ŏI�I�Ɉ��肷��Ȃ�A��nfn����lfp(f)
�ؖ�
�@(i) fn���̒�`���n��0�̂Ƃ��A
�@�@�@�@�@�@�@�@�@f(fn-1��)��fn-1���Ȃ�Afn��=fn-1�� �E�E�E�@
�@�@�@�@�@�@�@�@�@f(fn-1��)��fn-1���łȂ��Ȃ�Afn��=fn-1����f(fn-1��)�E�E�E�A
�@�@�@�@�@�@�ނ͏�E���Z�q�Ȃ̂�fn-1����fn-1����f(fn-1��)�E�E�E�B
�@�@�@�@�@�@�@�@�@�A�B���Afn-1����fn-1����f(fn-1��)= fn���E�E�E�C
�@�@�@�@�@�@�@�@�@�C���牽��̏ꍇ��n��0�̂Ƃ��Afn-1����fn�� �ƂȂ�A�㏸���ł���B
(ii)����m�ɑ���f(fm��)��fm���Ɖ��肷��B�A�[�@�ɂ��An��m�ɑ���fn��=fm���ł��邱�Ƃ������F
�@f(fm��)��fm����fn���̒�`����@���fm+1��=fm�� ����������B���������āAn=m+1�̂Ƃ��Afn��=fm�� ����������Bn=k��m+1�ɑ���fk��=fm���Ɖ��肷��ƁAn=k+1�̂Ƃ��Af�̒P��������f(fk��)��f(fm��)�Af(fm��)��fm���Ȃ̂�f(fk��)��fm��=fk���ƂȂ�B���������āAfn���̒�`����fk+1��=fk���ƂȂ�B�����A���w�I�A�[�@�i���j�ɂ��n��m�ɑ���fn��=fm�����������邱�Ƃ��ؖ����ꂽ�B�܂��A(fn��)n�͏㏸���Ȃ̂Ł�nfn��= fn��= fm��
�@�@�i���j�Fn=m+1�̂Ƃ��������邱�Ƃ�������An=k��m+1�ɑ��Đ��藧�Ɖ��肷��ƁAn=k+1�̂Ƃ�
�@�@�@���藧���Ƃ������ꂽ�B
(iii) (fn��)n���ŏI�I�Ɉ��肷��Ɖ��肷��ƁA����́A����m�����݂��āA�C�ӂ�n��m�ɑ���
�@�@fn��= fm�����������邱�Ƃł���B�����ŁA�w���@�ɂ��f(fm��)��fm�����������Ȃ��Ƃ���ƁA
�@�@fn���̒�`��3�Ԗڂ̎�����������̂ŁAfm+1��=fm����f(fm��)�E�E�E�@
�@������fm+1��=fm���E�E�E�E�A�@
�@�ނ͏�E���Z�q�Ȃ̂�fm����f(fm��)��f(fm��)�E�E�E�E�B
�@�@�A�B����Afm+1����f(fm��)����͔w���@�̉���ɖ�������B
�@���������āAf(fm��)��fm������������B
(iv) (fn��)n���ŏI�I�Ɉ��肷��Ȃ�A(iii)����f(fm��)��fm���ƂȂ�悤��m�����݂���B(ii)���
�@f(fm��)��fm���ƂȂ�悤��m��n��m�ɑ��āA��nfn��= fm������������B
�@f(fm��)��fm�����Afm����Red(f)�ł���A�^���X�L�̕s���_�藝���lfp(f)=��Red(f)��fm��
�@�@���������āAfm��=��nfn�ށ�lfp(f)�ƂȂ�B�@�@�@�@�@�@�@�@�@�@�@��
�ȏ�̏����iFact4.14)�����Ƃɖ���S�C�P�R�̏ؖ������L�Ɏ����G
�ؖ��@�w���@�ɂ��ؖ����邽�߁A�㏸��(fn��)n�͌����Ĉ��肵�Ȃ��Ɖ��肷��B���Ȃ킿�A
�C�ӂ�n0�ɑ��Ĉ���n��n0�����݂��āAfn����fn0���E�E�E�@ �Ƃ���B
�㏸��(fn��)n�͌����Ĉ��肵�Ȃ��Ȃ�AFact4.14(ii)���C�ӂ�n��0�ɑ���f(fn-1��)��fn-1���͐������Ȃ��B�����fn���̒�`���牺�L���������邱�Ƃ��Ӗ�����G
fn��=�ہ@(n=0�̂Ƃ��j�@�@fn��= fn-1����f(fn-1��)�@�in��0�̂Ƃ��j
���A�V�[�P���X(ln)n�����L�ɂ���`����G
�@�@�@�@�@�@�@�@�@�@ln=�ہ@(n=0�̂Ƃ��j�@ln= f(fn-1��)�@�in��0�̂Ƃ��j
(ln)n�͏㏸���ƂȂ�(��Fact4.14(i)���(fn��)n�͏㏸���ł���Af�͒P���Ȃ̂Łj�B
���ɁA�C�ӂ�n�ɑ��āAln��=fn�����������邱�Ƃ𐔊w�I�A�[�@�ɂ�莦���G
n=0�̂Ƃ��A���̎��͐�������i��l0��=l0=�ہAf0��=�ہj�B
n-1�ɑ��Đ�������Ɖ��肵�An��0�̏ꍇ���l����B��`���Aln��=ln-1����ln�@
n-1�ɑ���ln-1��=fn-1���Ȃ̂ŁAln��=ln-1����ln = fn-1����ln= fn-1����f(fn-1��)= fn��
���������āA�C�ӂ�n�ɑ��āAln��=fn������������B
����A(ln)n�͏㏸���Łނ�widening���Z�q�Ȃ̂ŁA(ln��)n�͍ŏI�I�Ɉ��肷��B
���Ȃ킿�A(fn��)���ŏI�I�Ɉ��肷��B����͍ŏ��̉���ɖ�������B
���������āA �㏸��(f n��)n�͍ŏI�I�Ɉ��肷��B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|�@�ȏ�@�|