中央遮蔽のある開口の回折像について
2014年10月 舟越 和己
1.中央遮蔽とは
下の図のように、開口(注)の中央にある円形の遮蔽のことで、具体的には反射望遠鏡の
斜鏡やカタディオプトリック系の副鏡が該当します。

(注)望遠鏡が天体から最初に光を集める範囲を「開口(aperture)」 と言います。
■遮蔽率ε
開口の直径Dに対する遮蔽の直径の比率を遮蔽率εと言います。
遮蔽率の二乗は、遮蔽が開口に占める面積比となります。
(例)ε=0.316とすると、遮蔽の開口に対する面積比=(0.316)2=0.0999=10%
■中央遮蔽による回折像
中心の明るいディスクをエアリーディスク、それを囲むリングを回折リングと
言いますが、「第一回折リングの強度は遮蔽が大きくなるにつれて増大(第二
回折リング以降は遮蔽率による)」します。
→本資料は、この理由について以降で説明します。
2.フラウンフォーファー回折理論の結果(注)から
(注)回折理論について知りたい方は別紙の「フラウンフォーファー回折紹介」を
参照して下さい。
■対象とする開口
中央遮蔽の回折像を理解するために、次の3つのタイプの開口を考えます。
εは遮蔽率です。

■回折理論による回折像の表現
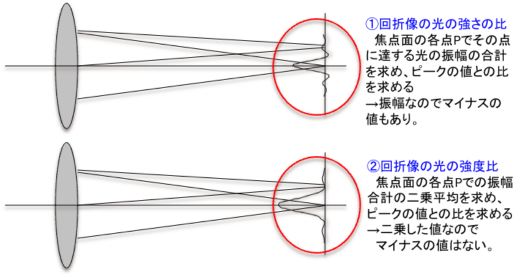
これには、(1)集った光の強さ(振幅の合計)の比と (2)集った光の強度比((1)の二乗平均)
という2種類の表現があります。
■開口の大きさと回折像の関係
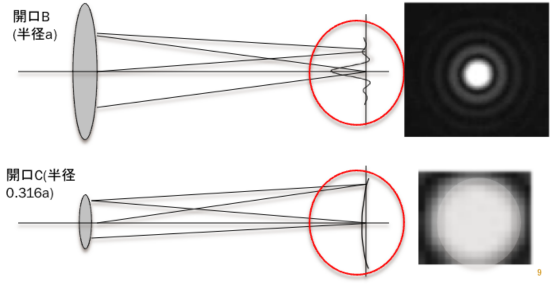
開口が小さいほど回折像の光の強さは弱くなり、回折像のサイズは大きくなります。
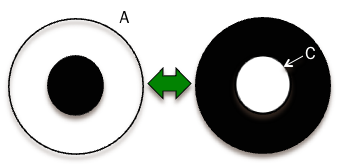
■互いに相補的な遮蔽とは?
図のように、透明部と不透明部が逆転している遮蔽のことです。
■互いに相補的な遮蔽の光の振幅(光の強さ)には次のことが成立します;
「互いに相補的な(透明部と不透明部が逆転している)2つの遮蔽が置かれた
とき、これによって任意の点に生ずる回折光の振幅の和は、遮蔽が全くない
ときにその点に生じる振幅に等しい」
⇒従って、下記が成立します(これを「バビネの原理」と言います)。
●中央遮蔽による回折光の振幅=(無遮蔽による回折光の振幅)
-(遮蔽と同じサイズの開口による回折光の振幅)
→この意味は?
図を使って説明すると、下記の赤丸の部分の光の強さ(振幅)の差です。
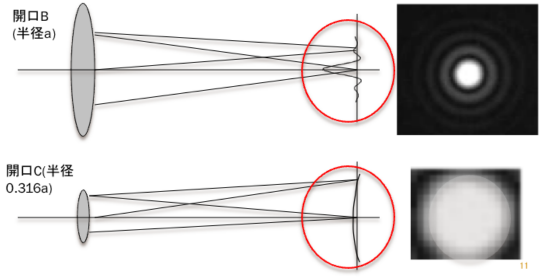
もっと分かり易くするために赤丸の部分を拡大すると、次のようになります。
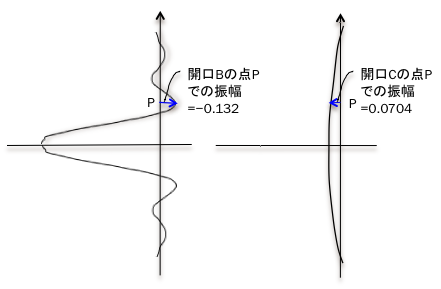
「差分をとる」とは、図の矢印の大きさの差です。
(例)図の点Pで、開口Bの振幅が-0.132、開口Cの振幅が0.0704とすると、それらの振幅の差は、
-0.132-0.0704=0.2024
となります。
この例のように、振幅の差の絶対値が開口Bの振幅の絶対値よりも大きくなることがあります。
→中央遮蔽の第一回折リングが無遮蔽のそれよりも明るくなる理由はここにあります。
3.中央遮蔽の回折像を求める
■開口Bと開口Cの回折光の強さの分布
下の図は半径a無遮蔽の開口の中心の光の強さを1としたときの開口Bと開口Cの回折光の
強さの分布です。

■マイナスの回折
●中央遮蔽による回折光の振幅=(無遮蔽による回折光の振幅)
-(遮蔽と同じサイズの開口による回折光の振幅)
の式の引き算の項の代わりに、遮蔽をマイナスの回折と考えて、
●中央遮蔽による回折光の振幅=(無遮蔽による回折光の振幅)
+(-[遮蔽と同じサイズの開口による回折光の振幅]) ・・・(1)
という回折の合成にします。
遮蔽がマイナスの回折になるとは?→下の図のように開口に蓋をするような遮蔽
からの回折像の振幅は逆転すると考えます。

■中央遮蔽の開口の回折像の求め方
上記の(1)式により、2つのグラフの振幅の値を加えて二乗を計算したものです。
すなわち、
{(無遮蔽による回折光の振幅)+(-[遮蔽と同じサイズの開口による回折光の振幅])}2
→これは中央遮蔽のある開口の回折光の強度比になります。
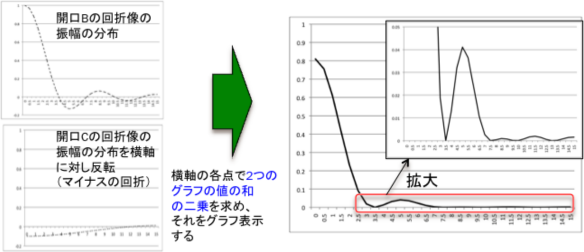
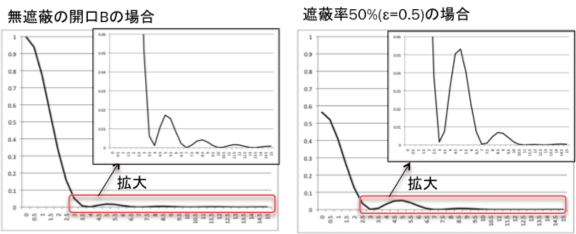
■以上のことから、無遮蔽の場合と中央遮蔽のある場合の回折像の強度比を比較します。

→2つの図の拡大から分かるように、第一回折リングは中央遮蔽のある方が光の強度が
大きくなっています。第二回折リングは無遮蔽の方が強度比大、等の違いがあります。
■以上は、遮蔽率ε=0.316でしたが、遮蔽率50%(ε=0.5)とすると、右下の図のように
ピークの強度が低下し、第一回折リングの強度がさらに増加します(第二回折リングの
強度もやや増加)。
【参考資料】 月刊天文 1994年7月号 P.54-55 回折像と二重星
以上で終わりです。