はじめに
ファジィ理論を二重星分離の難易度に適用した「Fuzzy
Splitting」の日本語訳を以下に載せます。
→原文紹介に本日本語訳の紹介(This article is also available in Japanase, thanks
to a
translation by Mr. Kazumi Funakoshi)とリンクがあります
ここで「Fuzzy Splitting」を日本語に訳すのを快諾して下さった著者 氏に
氏に
感謝致します。[ I would like to express my deeply gratitude to Mr.
for permitting translation to Japanese.]
ファジィ・スプリッティング(Fuzzy Splitting by
 )
)
著者(Auther): →著者紹介はこちら
→著者紹介はこちら
日本語訳(Translation to Japanese):Kazumi Funakoshi
ファジィ論理(FL)は、今日ホットな話題です(訳注1)。1965年にバークレー校のザデー教授の
仕事に始まり、この理論は今日大きく受け入れられています。特に日本では無人ヘリコプターから
ビデオカメラまでいろんなものに適用されています。おそらく気が付いていないかもしれませんが、
車の運転やテレビを見ること或いは朝ヒゲを剃ることでさえもファジィ論理のテクノロジーが使わ
れているのです。ここではファジィ理論を紹介し、これを二重星の分離の難しさを知るためのシス
テムに適用します。
離角が10秒の二重星は開いていて、離角がわずか1秒の二重星はぴったり寄り添っているという
ことは誰でも同意できると思います。さて、こういう質問をしたらどうでしょう。「1秒から10秒
の範囲であなたは寄り添っていると開いている表現をどこで変えますか。」
あなたは、しばらくして「あまり確信はないが多分中間点の5秒くらい。」と答えるかもしれません。
この回答は、新たな煩わしい問題を引き起こします:この分類では、Cp 13(離角=5.1秒)は開いて
いてCor 148(離角=4.8秒)は寄り添っているとなりますが、この突然の変化は二重星の観測者の経験
とうまくフィットしません。
あらゆる時代を通しての最も偉大な二重星観測者の1人であるウィルヘルム・ストルーベは、同様
の問題に苦しみ、Catalogus Novus(1827)において二重星を離角により分類しました:4秒以下は
タイプI、4秒から8秒まではタイプII、8秒から16秒はタイプIII、16秒から32秒はタイプIV。
ストルーベは、こういう明確な分類にも問題があることを認識してタイプをさらにタイト,非常に
タイト,極めてタイトに分けました。
こういう細分化はしばらくの間は問題を沈静化するかもしれないが解決にはなりません。
面白いことに、我々は他の人と数学的ではないが経験的知識に基づいて言語学的用語でコミュニ
ケーションをする傾向にあります。昨夜の二重星の観測について話している二人のアマチュア天文
家の状況を想像して下さい:
「ジョ−、私は昨日の観測は琴座のイプシロン(ダブル・ダブル)を観ることから始めました。
知っての通りこれはやや接近したコンポーネントを持つ素敵な二重星系です。その後、牛飼座の
オットーストルーベ298(離角=1.0秒、光度は同じ7.5等)に望遠鏡を向けましたが、分離するの
が大変でした。」
「分りますよ、マーク。STF 298は本当にタイトな二重星なんだから。」
ジョ−とマークは彼等の観測を表現するのに数値について話す必要はありません。彼等はやや近い
とか非常にタイトのような平易な言葉を交換し、それらが二重星の分離に関連する話に非常に有効
になっています。こういうことを表現するを数学が許さないとしたら実に残念だと思いませんか?
でも御心配なく、これからファジィ集合の理論(FST)という美しい世界へ入りましょう。
ファジィ集合の理論(「ファジィ論理」は、ファジィコントロールからファジィ統計学までFSTに
関係したものの総体を表現する)の中心概念は、”排中律”の除外に基づいています。アリストテ
レスの時代から私達はデジタルな数学的モデルで育ってきました:人は背が高いか低いか、車は
早いか遅いか、物は安いか高いか、全てのものは黒か白か。にもかかわらず実際の世界は様々な
グレーの微妙な違いから成っています。それでは、二重星分離のためのファジィ分類を説明しま
しょう。新しい強力な概念を聞くことになると思いますので、少し注意を払って下さい。私は、
誰もがこれを簡単に理解することが出来ると思います。
ファジィ化
図1は、「二重星分離」の概念を表現する言語学的な変数を表しています。言語学的な変数は、
単純にいくつかのファジィ集合の集まりです。ここで使われるファジィ集合は、「非常にタイト(Very
Tight)」,「かなりタイト(Rather Tight)」,「タイト(Tight)」,「少し開いている(Open Tight)」,
「やや開いている(Bit Open)」です。ファジィ集合がどんなものかを見るため、「非常にタイト」と
いう表現を例に取り上げます。

図1 「離角」に対する言語学的な変数
図を見ると分るように、図の左端に位置している三角形の上には「非常にタイト」というラベル
があります。この三角形の底辺は1.0秒から3.0秒なので、離角が1秒から3秒の間にある二重星は
「非常にタイト」と定義されます。ここで、三角形の上の方の頂点は1.0秒を通る垂直軸の上にある
のが分ります。FSTでは、「非常にタイト」な二重星のファジー集合のメンバーシップ値は、離角
が1.0秒の時最も高いと云います。メンバーシップ値は、この直角三角形の斜辺に沿って行くと
減少し、離角が3.0秒の時ゼロになります。これがファジィ論理の中核:全ては程度の問題です。
次に、「かなりタイト」の表現について見てみます:この場合1.0秒から開始し、メンバーシップ
値は2.0秒で最大となり4.0秒でゼロになります。「分離」の言語学的な変数の残りのファジィ集合
も同様に記述出来ます。ファジィ論理適用のコンセプトを実際の二重星ストルーベ 3050で記述し
てみます。
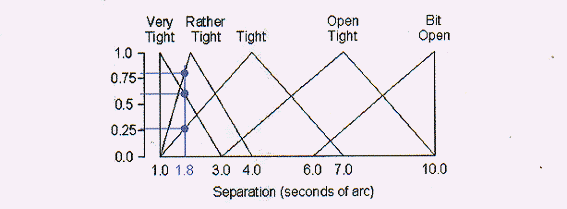
図2 ストルーベ 3050の分離に関するメンバーシップ値
この星はアンドロメダ座のほんとうに素晴らしい二重星で、その離角は1.8秒です。
図2の様に、この場合のメンバーシップ度は以下になります:
二重星として「かなりタイト」のファジィ集合に対して0.8
二重星として「非常にタイト」のファジィ集合に対して0.6
二重星として「タイト」のファジィ集合に対して0.26
この手法により、二重星を離角で分類することによる突然の変化なしに分離の概念を記述すること
ができます。また、このモデルのもとでストルーベ 3050は、異なる値のメンバーシップ値ですが
同時に「タイトな二重星」、「かなりタイトな二重星」及び「非常にタイトな二重星」となります。
このことは、様々な口径の望遠鏡で観測した時の印象の表現でも見ることができます。2.5インチの
屈折ではストルーベ 3050は非常にタイトな二重星であるのに8インチSCTのオーナーにとっては
タイトですが分離するのに特別難しいというわけではありません。
二重星分離の難しさをさらに進んで評価するために、観測者は主星と伴星の明るさを考慮に入れま
す。これは、分離の難しさを知るのに重要な役割を果たします。離角の場合と同様の方法により、
「等級差」の概念に対して容易に言語学的な変数を構築することができます。図3をこれの表現と
して見て下さい。あなたはもうこのファジィというゲームを楽しむことができるようになったと思
います。
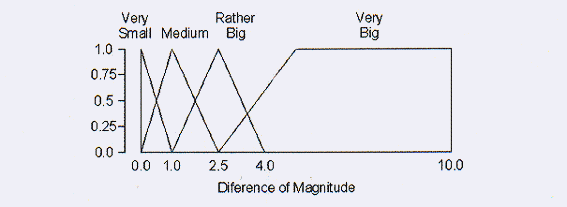
図3 「等級差」に対する言語学的な変数
ルール、どこでもルール!
もしジョ−とマークに二重星分離の難しさについてさらに進んでどんなことを知っているかを尋ね
たとしたら、あるエキスパート・ルールの適用のことを話すでしょう。例えば、
”もし離角がかなりタイトで等級差が中程度ならば、その二重星の分離はかなり難しい”
ジョ−とマークは忍耐強い愛すべき人たちなので、離角と等級差に対する言語学的な変数の可能な
組み合わせを記述するテーブルを書いてくれました。離角は列に、等級差は行に表してあり、以下
の様なテーブルです:
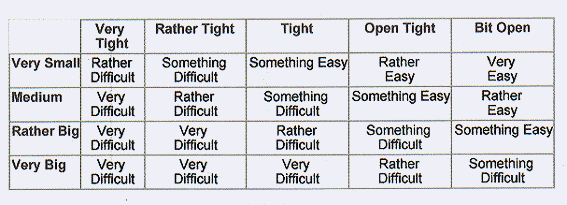
テーブル1a エキスパート・ルール
私達はすでに離角と等級差を記述するファジィ集合を持っていますが、難しさについてはまだ何も
言っていませんでした。そこで、難易度指数(DI)を記述する新たな言語学的な変数のモデルを作
成します。ここでDIは0.0から100.0までの値をとり、DIが0はどんな望遠鏡でも分離できる二重星、
DIが100.0はシーイングが良い日に優秀な望遠鏡を使い分離できる二重星を意味します。ジョ−と
マークから与えられたテーブルから、困難さのファジィ集合に「非常に易しい」「かなり易しい」
「やや易しい」「やや難しい」「かなり難しい」「非常に難しい」というラベルを付けることが
できます。図4は、「難易度指数」の概念を表現しています。
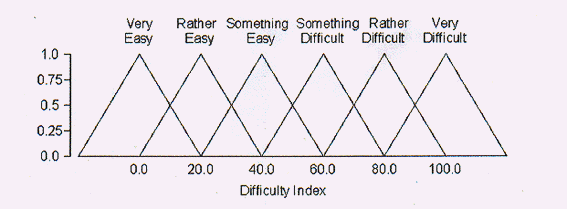
図4「難しさ」に対する言語学的な変数
インフェレンシング(推論)
ここでは、ファジィ論理をベースとしたシステムの「思考」がどこにあるかを示します。ドクター
レベルの数式が出て来ることがありますが、実際の観測の経験を事例にすれば容易になると思いま
す。獅子座ガンマ星アルギエバを例に計算してみましょう。少し疲れましたか?それではしばらく
リラックスしてこの二重星のペアの素晴らしい観測報告を読んで下さい。下記は、「Spirit of 33」
のメンバーであるBrendan Shawが2000年春に5インチフローライト屈折を使用して書いた記録
です:
「素晴らしい二重星。私の目にはオレンジと赤。149倍では2つの星の間にバスを走らせることが
できるようだ。シーイングが良くなる瞬間、そのペアの間の空間がクリアーブラックになった。
86倍ではトランプのカードが入るくらい、55では1枚の紙くらいの隙間。
倍率の低い2つのケースでは、ベストビューは星が雲に覆われるときにやってきた。明るいほう
の星のまぶしい光と回折リングがなくなり2つの分離された点像が55倍においてさえクリアー
になった。雲が薄くなると低倍率では2つの星がお互いにつながるようになる。2つが合流する
のではなく8の字のように。もし視野をすばやく流していたならそのペアを見逃していたかもし
れない。149倍では雲がなくても楽しい二重星。もし、片方の星の色がブルーだったら....北半球
のベスト33-doublesを誰か始めるならアルギエバは私の一票を得るでしょう。」

図5 アルギエバの分離に関するメンバーシップ値
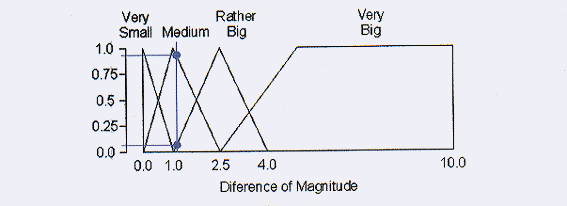
図6 アルギエバの等級差に関するメンバーシップ値
それでは講議に戻りましょう!。アルギエバは4.4秒離れたコンポーネントから成ります。各々は
2.5等と3.6等で輝いているので等級差は1.1です。図5と6は、「離角」と「等級差」に対する
メンバーシップ値がどのようにして得られるかを示しています。これらの値は下記の通り:
離角のメンバーシップ値:
タイト:0.87
少し開いている:0.35
等級差のメンバーシップ度:
中程度:0.93
かなり大:0.07
したがって、アルギエバは等級差が「中程度」で「かなり大」、離角が「タイト」で「少し開い
ている」となります。テーブル1aに表されているルールからどんなルールを適用したらようで
しょうか?すでに言語学的な変数に対して各々2つのファジィ集合を「狙い打ち」しているので、
これらに対して起こりうるすべての組み合わせを考えます:
離角が「タイト」で等級差が「中程度」
離角が「少し開いている」で等級差が「中程度」
離角が「タイト」で等級差が「かなり大」
離角が「少し開いている」で等級差が「かなり大」
テーブル1bは、この部分が分るように難易度指数を評価するため4つのルールを太字で表して
います。これはファジィ論理の重要な手法です:伝統的な旧来のシステムでは、一度に一つの
ルールしか成立しないのに対し、ファジィ論理は並列処理モードで動作できます。
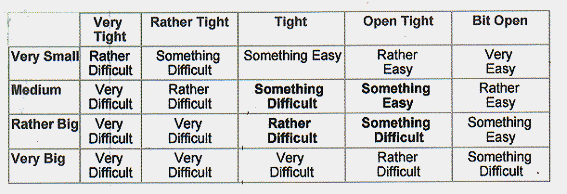
テーブル1b アルギエバを評価するためのルール
今、新たな質問が発生します:「いくらか易しい」、「いくらか難しい」及び「かなり難しい」
というファジィ集合にはどんなメンバーシップ値が適用されますか?ファジィ論理は、「ファジィ
共通集合」演算を記述するためのいくつかの手法を提供しています。このうち最も有効なのもは
「最小値」です。アルギエバに対する最初のルールについてこれを見てみましょう:
もし離角がタイトで等級差が中程度ならば難しさは「いくらか難しい」
今、太字のタイトと中程度というファジィ集合をメンバーシップ値で置き換えてみます:
もし離角が0.87で等級差が0.93ならば難しさは「いくらか難しい」
ここで、0.87と0.93のミニマム値は0.87です。そこで論理学の[モダス・ポネンス(訳注2)]と
呼ばれる推論を使うと、ファジィ集合「いくらか難しい」のメンバーシップ値は0.87となります。
言い換えると、アルギエバに対する最初のルールは次のようになります:
もし離角がタイト(0.87)で等級差が中程度(0.93)ならば難しさは「いくらか難しい」(0.87)
アルギエバに関係するすべてのルールに対し、同様にしてテーブル1Cを得ることができます:
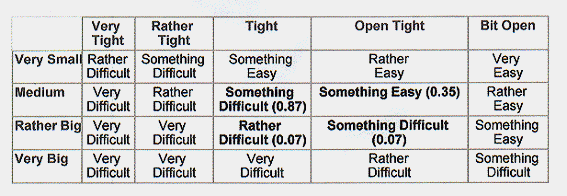
テーブル1C 重み付けられたルール
すなわち、アルギエバは以下のメンバーシップ値で表される難易度指数を持つ:
いくらか易しい:0.35
いくらか難しい:0.87
いくらか難しい:0.07
かなり難しい:0.07
あなたはこれをアルギエバの分離の難しさを評価する二重星のエキスパート委員会(ジョ−と
マークももちろん含まれている)から来た4人のメンバーと見ることができます。最初のメン
バーは、分離を「いくらか易しい」と云い、その信頼度は0.35。同様に他のエキスパートは
各自の意見を云い、信頼係数を与えます。このように、ファジィ論理は真に民主主義的な
システムですが、アルギエバに対する評決が必要です。幸い、エキスパート委員会は最終結果
である0から100の値をとる難易度指数を作り上げるわざを持っています。
脱ファジィ化
ファジィの世界から「ノーマル」な世界へ戻るためには、メンバーシップ値の集まりを数値と
しての表現に変換する必要があります。結局、ほとんどすべてのファジィシステムは出力と
して実際の値が必要となります。(例えば、車のエンジンに必要な燃料のグラム/分の値は、
もしあなたの車が日本で製造されていてファジィシステムによって計算されていたとしても
測定出来る量となります。
これを実現するためにはファジィ設計者に有効ないくつかの方法があります。私自身も1998
年にそのひとつを開発し、私のオフィスで東京工業大学の菅野道夫教授と話をして、教授が
それをすでに10年前に開発していたのを知るまでは私の研究に非常に満足していました。
重要な概念は、難しさのメンバーシップ値を重みとして扱い、各ファジィ集合を表す三角形の
底辺の中央値にこの重みを位置付けることです。下の図7はこれを明快に表しています:
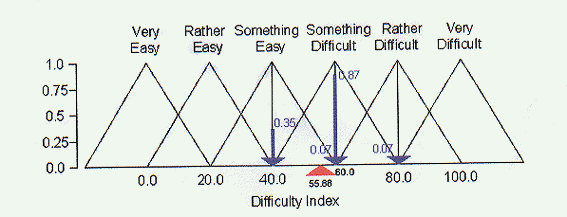
図7 脱ファジィ化
垂直方向の矢印で重みが表され、その長さはメンバーシップ値と関連づけられた「重み」を
表現しています。
今、これらの重みを平衡させる水平軸上の点を見つけたらどうでしょうか??これが菅野の
「シングルトン(訳注3)」モデリングを使ったファジィシステムの出力です。図では上に
向かった赤い矢印で表現されています。この脱ファジィ化の手法は直観的で計算しやすいと
いう利点があります。この脱ファジィ化の数式表現は以下の通りです:
X=Σ(Wi・Xi)/Σ(Wi)
ここでXは最終結果(難易度指数)、Wiは重み(メンバーシップ値の出力)、Xiは重みが適用
される水平軸上の点です。この式にアルギエバの値を代入すると、
DI=((0.35*40)+(0.87*60)+(0.07*60)+(0.07*80))/(0.35+0.87+0.07+0.07)
したがって、
DI=55.88
これが獅子座ガンマに対して得られた難易度指数です。おわかりのようにこれを手計算で行な
うとすると多数の計算が要求されますが、幸いなことにコンピュータというものがあります!
LADICが手助けする!
ファジィシステムをデザインし走らせるプログラムを製作・テストした後、設計者は通常
「制御面」と呼ばれるものを作ります。これは、変数(ここでは「離角」と「等級差」が
変数)の値の可能な組合せに対してその出力値を関係付けたサンプリング値です。
制御面はポータブルでコンパクトという利点があり、これらの値を電子チップに入力する
ことは電子エンジニアにとって子供の遊びのようなものです。私は、離角と等級差の範囲を
100の部分に分割して二重星のDIシステムのための制御面を作ることにしました。これら
の分割は10,000点の格子を生成し、各点に対してDIが計算され10,000個の3次元の点の
集まりが作られます。(私の旧式のコンピュータでは約3分かかりました)
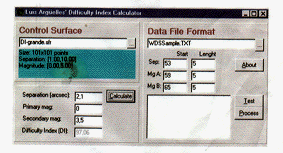
図8 LADICプログラム
あとは簡単です。Spirit of 33のメンバーであるラファエル・バーバラ氏は、この制御面
を読み込んで格子点に一致しない点を補間するプログラムを書きました。その結果がLADIC
と呼ばれるプログラムです。これはダウンロードして自由に使うことができます!ただし、
LADICユーザマニュアルを読むことをお忘れなく。
DI説明
以上の説明を読んであなたは私を見て真剣にこう言うかもしれません。
「理論は正しいように思えますが、現実の世界では私は6インチの屈折を持っています。この
望遠鏡の到達可能なDIはいくつですか?」
あなたの質問に答える前に、DIは多かれ少なかれ与えられた二重星の固有の性質を記述して
いることを認識しなければなりません。このことから私達は、DIと口径だけでなく、望遠鏡
の光学精度や観測サイトの平均シーイング条件、さらに二重星観測者としての経験といった
ものとの関係を確立する必要があります。
私達は「4インチ屈折のDIはXである」と単純に言うことはできません。その理由は、与えら
れた4インチの光学精度(二重星の観測にとって口径と同様に重要な要素)、観測地点のシー
イング(チリのアタカマ(訳注4)に住んでいる4インチ屈折のユーザは、例えばニューヨーク
市の観測者と異なるDIに到達するでしょう)そして観測者の経験に依存するからです。同じ
望遠鏡が与えられたとき、クートウやコメラス、スーザン・フレンチ、シィシィ・ハ−ス
(訳注5)のような観測者はあなたや私より上のDIに到達するでしょう。
LADICやSpirit of 33のサイトのDIが75から100の二重星を選んだ観測プログラムのテーブル
を使うにあたっては、シーイングの悪い夜は避けて標準的なシーイングの夜にあなた自身の
二重星のセットを観測して下さい。このとき、二重星を分離したらその星の名前とDIを記録
するのを忘れないように。こうして何回かの観測の後、あなたの観測システムで到達できる
上位のDIを5〜10個選び、その平均を計算して下さい。この値はあなたの参考値となり、
二重星の分離の難しさを評価するための最良のシステムとなるでしょう。
最後に、私はすぐれた補間プログラム(これは、7秒以下のワシントンダブルスターカタログ
を全て生成することができる)を書いただけでなく、この記事を書くことを勧めてくれた
ラファエル・バーバラ氏に心から謝意を表したいと思います。
(訳注1)日本では1987年に第一次ファジィブーム(予見ファジィ制御による仙台市の地下鉄
営業運転が始まった頃)、1990年に第二次ファジィブーム(家電品にファジィ制御
が応用された頃)がありました。
(訳注2)モダス・ポネンス:事実Aと規則A→Bがともに真であるとき、結論Bが真であること
を導く推論。
(訳注3)シングルトン:或る1点上のメンバーシップ値を除いて0となるファジィ集合のこと。
(訳注4)アタカマ:アンデス高地にあるアタカマ砂漠のことだと思われます。(星が良く見え
る場所の例)
(訳注5)クートウ:→Couteau:フランスの優れた二重星観測者の1人。
コメラス→Jose Luis Comellas:スペインの優れた二重星観測者。
スーザン・フレンチ→Susan French:二重星を愛する非常によく知られた観測者。
スカイ&テレスコープ誌のマンスリーセクションを書いている。
シィシィ・ハ−ス→Sissy Haas:二重星観測者。スカイ&テレスコープ誌に二重星
観測の記事を書いている。
Back to the HP Top page










