無遮蔽反射について BACK TO THE TOP PAGE
1.軸外しニュートン反射(Off-Axis Newtonian reflector)
軸外しニュートン式反射とは放物面鏡の光軸を外した領域を切り出し、主鏡とした
無遮蔽の反射望遠鏡です。

これは反射望遠鏡の偏芯絞りと同じではないかと思われがちですが、偏芯絞りだけ
では軸外しニュートンの光学性能を十分発揮できません。
→このことについては、下記3の軸外しニュートンの光学的性質を参照。
2.軸外しニュートン反射の製品
無遮蔽の反射について調べていたら軸外しニュートン反射というのが過去販売されて
いたというのが分かりました。
Astronomy Magazineの2009年5月号にDGM Optics OA-3.6 off-axis
reflectorのレビュー記事があるので2009年頃は販売されていたということです。
DGM Optics OA-3.6ATS off-axis reflector
3.軸外しニュートン反射の光学的性質
この光学系についてはTelescope Opticsの下記に詳しく載っています;
https://www.telescope-optics.net/tilted3.htm
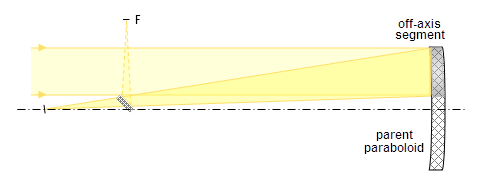
Off-axis Newtonianの光路図(Telescope Opticsより) 親の放物面鏡の部分を使用。
これを読むとこの光学系は、視野の中心部はニュートン式と同じく無収差です(放物面鏡
の一部を使用しているので当然ですが)。
周辺はニュートン式ではコマ収差が現れるのに対し、この軸外しニュートンは非点収差
が現れます。Telescope Opticsではこのことが図や式を使って説明されています。また、
焦点面が少し傾くのでその分を調整するとベストな像が得られるとあります。
スポットダイアグラムは、4インチf/10の軸外しニュートンで中心から0.3度の調整前と調整後
の例が載っています。調整後の例を見るとかなり良さそうです。
視野の中心では無収差というのは、同じ無遮蔽のハーシェル式と比べた場合、利点です。
軸外しニュートンの光学的性質についてさらに調べてみました。
光軸に平行な光線から成る波面(①)が放物面鏡に反射すると焦点に収束する
球面波面(②)となります。
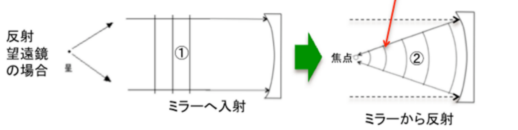
上記のことは軸外しニュートンの場合も同じで光軸に平行な入射光の光路で焦点F
に集まります。アイピースで覗くと視野の中心の像になります。
一方、視野の中心から外れた像は斜めに入射する光から形成されます。斜めに入射する
光が放物面鏡に反射すると球面波面ではなく下記のようなS字型の波面となり収束します。
→この結果、ニュートン式望遠鏡の視野の周辺は「コマ収差」が現れます。

一方、軸外しニュートンの波面は上記S字の上半分の形状になります。
→この結果、軸外しニュートンの視野の周辺は「非点収差」が現れます。
このため周辺像を最良焦点にしようとすると焦点面に傾きが生じます。フォーカサ―の
位置も少しシフト(下の図のBest image surface)。→ベストな像を得るためにはこの調整
が必要(角度で4~5度)。
→このことから、「偏芯絞りだけでは軸外しニュートンの光学性能を十分
発揮できない」ことがわかります。

以上はTelescope Opticsより
ここで疑問点;
DGM Opticsの軸外しニュートン望遠鏡は上記補正をどう実現しているのでしょうか。
また、軸外しの放物面鏡はどうやって製作しているのでしょうか。
→ED Ting氏のTelescope ReviewにOff-axis mirrorについての記述があります;
https://www.scopereviews.com/page1f.html#3
DGM Optics's off-axis mirrors are cut, like a cookie cutter, out of a larger "parent" mirror.
If done correctly, one parent mirror can yield as many as four smaller off-axis mirrors.
This is not as easy as it sounds. First, you have to locate an exceptional mirrorof 16"
or so in diameter. Then, you need the skill to cut them without stressing the glass.
→親の放物面鏡から切り出すようですが、これをストレスフリーに行うのは
容易でないようです。
また、下記は重要なコメントです;
https://www.cloudynights.com/topic/657948-does-an-off-axis-aperture-equal-an-apo-of-same-size/
Another note: In other threads on the topic, it's often pointed out that in order to get
the off-axis mask to perform to it's potential, the secondary mirror should be realigned
to point to the center of the off-axis aperture. Then, the focuser should be tilted to maintain
the 90deg angle to this new, tilted axis. I have no idea to what extent this impacts performance,
and I didn't do this with my masks. However, these features are built in to the OA-4,
so it's reasonable, I think, to assume it's fairly important.
■軸外しニュートン反射について書かれた本
Neil English著のChoosing and using a Dobsonian Telescope
のP.90~93にOff-axis reflectorのことが書いてあります。
4.ハーシェルニュートン式反射
同じTelescope Opticsにハーシェル式反射が載っています。
https://www.telescope-optics.net/tilted2.htm

ハーシェル式の派生型(ハーシェル・ニュートン)の光路図(Telescope Opticsより)
これを読むと、次のようなことが書いてあります(内外像やMTF図の部分はStar Testing
Astronomical Telescopeより)。
ハーシェル式反射は鏡が傾いているので中心でも非点収差が残ります。このため、中心で
焦点内外像は少し楕円形となり内像と外像は楕円の方向が直角になります(下図)。
これを出来るだけ小さくしようとすると非常に大きなF値となります。下の方の式にあるように
D=100mm,ζ=0.6, RMS波面精度ωa=λ/14(≒P-Vではλ/4、すなわちストレール値=80%)
ならばF=22.3が必要です。ストレール値80%はディフラクションリミテッドに達しているので
これで十分ですが、これをさらに2倍の精度RMS=λ/28(P-Vではλ/8, ストレー値=95%)に
するためにはF=28.3が必要です(口径10cmで3メートル近くの筒になるので現実的ではあり
ません。口径5cmでもRMS=λ/28(P-Vではλ/8)の波面精度を要求しようとするとF=22.4です)。
上記はζ=0.6を使用していますがζは下で説明しているように主鏡の傾きに関係する値です。
これを変えると傾きを小さくでき非点収差は小さくなりますが、斜鏡を入れるスペースとの関係
で制限があります。

3/8λの非点収差(P-V値)
また、非点収差によるコントラストの低下は下記のMTF図のようになります。例えば
P-Vでλ/4の非点収差による波面収差ならば下の図の3/8λより少し良いレベル。
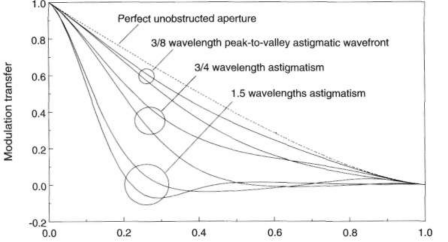
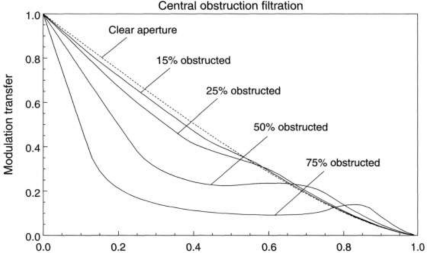
これを下記の中央遮蔽のMTFと比較すると25%遮蔽のコントラスト低下よりも少し
悪いように見えます。
→①ハーシェル式は無遮蔽だが中心で非点収差が残りコントラスト低下が発生。
②ニュートン式は中心で無収差だが中央遮蔽によるコントラスト低下が発生。
どちらを取るかは非点収差の量と中央遮蔽の遮蔽率によります。
非点収差の波面誤差をRMSでωaに収めるための条件(口径と口径比)は、
F=(D/128ωaζ2√24)^1/3.
ここで、ζは
"ζ is the relative distance in units of the primary focal length at which the ray reflected
from the mirror center breaks out of the path of incoming axial pencil"
です。すなわち、ミラーの中心から反射された光が入射光の経路から外れるとき焦点距離
からその距離(鏡から外れるまでの距離)を求める係数です。
例えば、D=100mm,ζ=0.6, ωa=λ/14(≒P-Vではλ/4、すなわちストレールレシオ=80%)
ならばF=22.3必要です。この時の鏡の傾きの角度はτ=1/(4ζF)により求めることができ
ます(単位はラジアン)。実際に角度を求めると、τ=1/(4*0.6*22.3)*180/π=1.07度となります。
D=50mm, ζ=0.6, ωa=λ/14(≒P-Vではλ/4)で計算すると、F=17.8となります。
実際にはコマ収差も少しある(RMS=λ/40)ので、トータルの波面誤差はRMS=λ/13.2と
なります。
以上はζ=0.6で計算しましたがミラーの傾きをもう少し小さくする(ζ=0.7等)波面誤差は
改善できるようですが、傾きを小さくし過ぎると斜鏡を付けるスペースが得られなくなります。
図133が始まる箇所
"but it does exceed this level in the best portion of the field (FIG. 133). ”
からの説明は不明点があります。
5.マクストフ・ハーシェル
D.D. Maksutovの1944年の論文
New Catadioptric Meniscus Systems, Journal of the Optical Society of America
を見ていると、マクストフ望遠鏡の例としてハーシェル型が載っていました。この型式だと
焦点距離が短くできそうです;
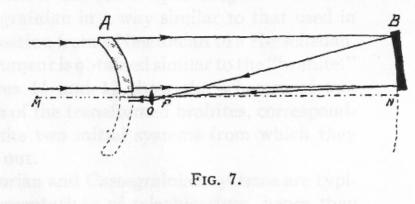
この型式の望遠鏡について関係する文献として下記があります;
Wright, Franklin B., "The Maksutov Lens Applied to Herschelian and Newtonian Telescopes",
in Volume 3 of "Amateur Telescope Making"
(参考)MTFカーブから見た無遮蔽と中央遮蔽の望遠鏡の違いについて
MTFカーブの縦軸は「対象のコントラスト」、横軸は「対象の模様の細かさを表しています。
「図解 MTFの話」にその考え方を説明していますが、簡単に言えば、MTFカーブは
天体望遠鏡で細かい対象を見るほど対称のコントラストが低下する、ということを表しています。
ここで、対称の模様が細かいとか荒いとかは「明暗のバー」の繰り返しの間隔で決まります。
一定間隔での繰り返し数を「空間周波数」と言います(詳細は「図解 MTFの話」参照)。
下の図は、①20cm屈折、②20cmで中央遮蔽34%の反射、③12cm屈折のMTFカーブを
描いたものです(いずれも無収差の完全な望遠鏡とします)。
横軸の単位(cycle/秒)は、1秒角の間に明暗が何サイクルあるかを示しています。
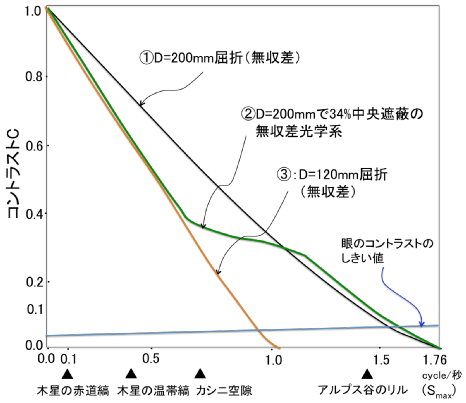
いずれのカーブも横軸を右に行くほど(すなわち、細かいも夜を見るほど)コントラストが低下します。
グラフの下に▲で書いてあるものは具体的な天体での空間周波数のおおよその値の例です。この例
では木星の赤道縞が最も空間周波数が低く、アルプス谷のリルが最も高くなっています。
20cm屈折①と20cm反射②のMTFカーブを見比べて下さい。すぐ分かることは、空間周波数が低い
ところから中くらいまでは②の反射望遠鏡は①の屈折望遠鏡に比べてコントラストが低くなっていると
いうことです。これらの周波数帯域は、星雲星団から惑星の主な模様を観察する倍率に対応しています。
次に、20cm反射②と12cm屈折③を比べてみて下さい。これを見ると低から中の空間周波数では、
ほぼ同じカーブになっています。つまり、20cm反射と12cm屈折は低倍率から惑星の模様を見る中倍率
位まではコントラストに関しては同程度ということです。
つまり、星雲星団から月の全景や惑星の主な模様の観察では、屈折望遠鏡が見え方のコントラストでは
断然有利ということです。中央遮蔽のある望遠鏡は、低から中までの空間周波数領域では無遮蔽の望遠鏡
(屈折、ハーシェル式反射、シーフシュピーグラー)にコントラストで負けます(注)。
(注)中央遮蔽率が小さくなるとコントラストの低下は改善します。そのため。昔から惑星用の
反射望遠鏡は中央遮蔽を小さくした(20%程度)作りになっていました。
一方、アルプス谷のリルのような細かい模様を見る場合は、空間周波数が非常に高いのでコントラストは
低下しますが、この周波数帯では反射望遠鏡③の方が屈折望遠鏡①よりコントラストが高くなります。
以上、屈折望遠鏡と中央遮蔽のある望遠鏡の違いをMTFカーブという観点から比べましたが、
これ以外にも比較する観点があります。
BACK TO THE TOP PAGE
1.軸外しニュートン反射(Off-Axis Newtonian reflector)
軸外しニュートン式反射とは放物面鏡の光軸を外した領域を切り出し、主鏡とした
無遮蔽の反射望遠鏡です。

これは反射望遠鏡の偏芯絞りと同じではないかと思われがちですが、偏芯絞りだけ
では軸外しニュートンの光学性能を十分発揮できません。
→このことについては、下記3の軸外しニュートンの光学的性質を参照。
2.軸外しニュートン反射の製品
無遮蔽の反射について調べていたら軸外しニュートン反射というのが過去販売されて
いたというのが分かりました。
Astronomy Magazineの2009年5月号にDGM Optics OA-3.6 off-axis
reflectorのレビュー記事があるので2009年頃は販売されていたということです。
DGM Optics OA-3.6ATS off-axis reflector
3.軸外しニュートン反射の光学的性質
この光学系についてはTelescope Opticsの下記に詳しく載っています;
https://www.telescope-optics.net/tilted3.htm

Off-axis Newtonianの光路図(Telescope Opticsより) 親の放物面鏡の部分を使用。
これを読むとこの光学系は、視野の中心部はニュートン式と同じく無収差です(放物面鏡
の一部を使用しているので当然ですが)。
周辺はニュートン式ではコマ収差が現れるのに対し、この軸外しニュートンは非点収差
が現れます。Telescope Opticsではこのことが図や式を使って説明されています。また、
焦点面が少し傾くのでその分を調整するとベストな像が得られるとあります。
スポットダイアグラムは、4インチf/10の軸外しニュートンで中心から0.3度の調整前と調整後
の例が載っています。調整後の例を見るとかなり良さそうです。
視野の中心では無収差というのは、同じ無遮蔽のハーシェル式と比べた場合、利点です。
軸外しニュートンの光学的性質についてさらに調べてみました。
光軸に平行な光線から成る波面(①)が放物面鏡に反射すると焦点に収束する
球面波面(②)となります。

上記のことは軸外しニュートンの場合も同じで光軸に平行な入射光の光路で焦点F
に集まります。アイピースで覗くと視野の中心の像になります。
一方、視野の中心から外れた像は斜めに入射する光から形成されます。斜めに入射する
光が放物面鏡に反射すると球面波面ではなく下記のようなS字型の波面となり収束します。
→この結果、ニュートン式望遠鏡の視野の周辺は「コマ収差」が現れます。

一方、軸外しニュートンの波面は上記S字の上半分の形状になります。
→この結果、軸外しニュートンの視野の周辺は「非点収差」が現れます。
このため周辺像を最良焦点にしようとすると焦点面に傾きが生じます。フォーカサ―の
位置も少しシフト(下の図のBest image surface)。→ベストな像を得るためにはこの調整
が必要(角度で4~5度)。
→このことから、「偏芯絞りだけでは軸外しニュートンの光学性能を十分
発揮できない」ことがわかります。

以上はTelescope Opticsより
ここで疑問点;
DGM Opticsの軸外しニュートン望遠鏡は上記補正をどう実現しているのでしょうか。
また、軸外しの放物面鏡はどうやって製作しているのでしょうか。
→ED Ting氏のTelescope ReviewにOff-axis mirrorについての記述があります;
https://www.scopereviews.com/page1f.html#3
DGM Optics's off-axis mirrors are cut, like a cookie cutter, out of a larger "parent" mirror.
If done correctly, one parent mirror can yield as many as four smaller off-axis mirrors.
This is not as easy as it sounds. First, you have to locate an exceptional mirrorof 16"
or so in diameter. Then, you need the skill to cut them without stressing the glass.
→親の放物面鏡から切り出すようですが、これをストレスフリーに行うのは
容易でないようです。
また、下記は重要なコメントです;
https://www.cloudynights.com/topic/657948-does-an-off-axis-aperture-equal-an-apo-of-same-size/
Another note: In other threads on the topic, it's often pointed out that in order to get
the off-axis mask to perform to it's potential, the secondary mirror should be realigned
to point to the center of the off-axis aperture. Then, the focuser should be tilted to maintain
the 90deg angle to this new, tilted axis. I have no idea to what extent this impacts performance,
and I didn't do this with my masks. However, these features are built in to the OA-4,
so it's reasonable, I think, to assume it's fairly important.
■軸外しニュートン反射について書かれた本
Neil English著のChoosing and using a Dobsonian Telescope
のP.90~93にOff-axis reflectorのことが書いてあります。
4.ハーシェルニュートン式反射
同じTelescope Opticsにハーシェル式反射が載っています。
https://www.telescope-optics.net/tilted2.htm

ハーシェル式の派生型(ハーシェル・ニュートン)の光路図(Telescope Opticsより)
これを読むと、次のようなことが書いてあります(内外像やMTF図の部分はStar Testing
Astronomical Telescopeより)。
ハーシェル式反射は鏡が傾いているので中心でも非点収差が残ります。このため、中心で
焦点内外像は少し楕円形となり内像と外像は楕円の方向が直角になります(下図)。
これを出来るだけ小さくしようとすると非常に大きなF値となります。下の方の式にあるように
D=100mm,ζ=0.6, RMS波面精度ωa=λ/14(≒P-Vではλ/4、すなわちストレール値=80%)
ならばF=22.3が必要です。ストレール値80%はディフラクションリミテッドに達しているので
これで十分ですが、これをさらに2倍の精度RMS=λ/28(P-Vではλ/8, ストレー値=95%)に
するためにはF=28.3が必要です(口径10cmで3メートル近くの筒になるので現実的ではあり
ません。口径5cmでもRMS=λ/28(P-Vではλ/8)の波面精度を要求しようとするとF=22.4です)。
上記はζ=0.6を使用していますがζは下で説明しているように主鏡の傾きに関係する値です。
これを変えると傾きを小さくでき非点収差は小さくなりますが、斜鏡を入れるスペースとの関係
で制限があります。

3/8λの非点収差(P-V値)
また、非点収差によるコントラストの低下は下記のMTF図のようになります。例えば
P-Vでλ/4の非点収差による波面収差ならば下の図の3/8λより少し良いレベル。

これを下記の中央遮蔽のMTFと比較すると25%遮蔽のコントラスト低下よりも少し
悪いように見えます。
→①ハーシェル式は無遮蔽だが中心で非点収差が残りコントラスト低下が発生。
②ニュートン式は中心で無収差だが中央遮蔽によるコントラスト低下が発生。
どちらを取るかは非点収差の量と中央遮蔽の遮蔽率によります。

非点収差の波面誤差をRMSでωaに収めるための条件(口径と口径比)は、
F=(D/128ωaζ2√24)^1/3.
ここで、ζは
"ζ is the relative distance in units of the primary focal length at which the ray reflected
from the mirror center breaks out of the path of incoming axial pencil"
です。すなわち、ミラーの中心から反射された光が入射光の経路から外れるとき焦点距離
からその距離(鏡から外れるまでの距離)を求める係数です。
例えば、D=100mm,ζ=0.6, ωa=λ/14(≒P-Vではλ/4、すなわちストレールレシオ=80%)
ならばF=22.3必要です。この時の鏡の傾きの角度はτ=1/(4ζF)により求めることができ
ます(単位はラジアン)。実際に角度を求めると、τ=1/(4*0.6*22.3)*180/π=1.07度となります。
D=50mm, ζ=0.6, ωa=λ/14(≒P-Vではλ/4)で計算すると、F=17.8となります。
実際にはコマ収差も少しある(RMS=λ/40)ので、トータルの波面誤差はRMS=λ/13.2と
なります。
以上はζ=0.6で計算しましたがミラーの傾きをもう少し小さくする(ζ=0.7等)波面誤差は
改善できるようですが、傾きを小さくし過ぎると斜鏡を付けるスペースが得られなくなります。
図133が始まる箇所
"but it does exceed this level in the best portion of the field (FIG. 133). ”
からの説明は不明点があります。
5.マクストフ・ハーシェル
D.D. Maksutovの1944年の論文
New Catadioptric Meniscus Systems, Journal of the Optical Society of America
を見ていると、マクストフ望遠鏡の例としてハーシェル型が載っていました。この型式だと
焦点距離が短くできそうです;

この型式の望遠鏡について関係する文献として下記があります;
Wright, Franklin B., "The Maksutov Lens Applied to Herschelian and Newtonian Telescopes",
in Volume 3 of "Amateur Telescope Making"
(参考)MTFカーブから見た無遮蔽と中央遮蔽の望遠鏡の違いについて
MTFカーブの縦軸は「対象のコントラスト」、横軸は「対象の模様の細かさを表しています。
「図解 MTFの話」にその考え方を説明していますが、簡単に言えば、MTFカーブは
天体望遠鏡で細かい対象を見るほど対称のコントラストが低下する、ということを表しています。
ここで、対称の模様が細かいとか荒いとかは「明暗のバー」の繰り返しの間隔で決まります。
一定間隔での繰り返し数を「空間周波数」と言います(詳細は「図解 MTFの話」参照)。
下の図は、①20cm屈折、②20cmで中央遮蔽34%の反射、③12cm屈折のMTFカーブを
描いたものです(いずれも無収差の完全な望遠鏡とします)。
横軸の単位(cycle/秒)は、1秒角の間に明暗が何サイクルあるかを示しています。

いずれのカーブも横軸を右に行くほど(すなわち、細かいも夜を見るほど)コントラストが低下します。
グラフの下に▲で書いてあるものは具体的な天体での空間周波数のおおよその値の例です。この例
では木星の赤道縞が最も空間周波数が低く、アルプス谷のリルが最も高くなっています。
20cm屈折①と20cm反射②のMTFカーブを見比べて下さい。すぐ分かることは、空間周波数が低い
ところから中くらいまでは②の反射望遠鏡は①の屈折望遠鏡に比べてコントラストが低くなっていると
いうことです。これらの周波数帯域は、星雲星団から惑星の主な模様を観察する倍率に対応しています。
次に、20cm反射②と12cm屈折③を比べてみて下さい。これを見ると低から中の空間周波数では、
ほぼ同じカーブになっています。つまり、20cm反射と12cm屈折は低倍率から惑星の模様を見る中倍率
位まではコントラストに関しては同程度ということです。
つまり、星雲星団から月の全景や惑星の主な模様の観察では、屈折望遠鏡が見え方のコントラストでは
断然有利ということです。中央遮蔽のある望遠鏡は、低から中までの空間周波数領域では無遮蔽の望遠鏡
(屈折、ハーシェル式反射、シーフシュピーグラー)にコントラストで負けます(注)。
(注)中央遮蔽率が小さくなるとコントラストの低下は改善します。そのため。昔から惑星用の
反射望遠鏡は中央遮蔽を小さくした(20%程度)作りになっていました。
一方、アルプス谷のリルのような細かい模様を見る場合は、空間周波数が非常に高いのでコントラストは
低下しますが、この周波数帯では反射望遠鏡③の方が屈折望遠鏡①よりコントラストが高くなります。
以上、屈折望遠鏡と中央遮蔽のある望遠鏡の違いをMTFカーブという観点から比べましたが、
これ以外にも比較する観点があります。
BACK TO THE TOP PAGE