光学精度のこと（続き）　　　　 　　　　　　　　　　　　 May 28,2000　　
　　光学精度の続きとして、光学系に対する大気の影響の関係について少し考えてみます。この内容は、
 私の個人的メモなので参考程度でみて下さい。

　（１）対象モデル
　　　大気の影響を考えるために下記のモデルを設定します。
　　

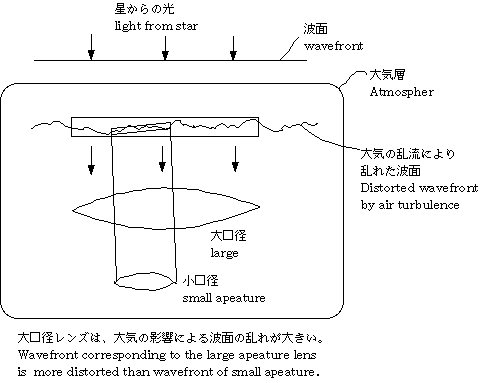
　　　星からの光が観測者に届く途中には、大きく分けて大気と望遠鏡を考える必要があります。そこで、
   上の図のように、大気系と望遠鏡系の２つのシステムを設定します。（実際には、望遠鏡の筒内気流、
   望遠鏡を設置している地面付近の気流状態等も考慮する必要がありますがここでは問題を単純化して
   大気と望遠鏡の対物レンズ（叉は主鏡）のみを考えます。）星からの光は、平行な波面として、大気を
   通過し、次に望遠鏡システムを通り観測者の目に達します。大気系では、air turbulenceと呼ばれる
   気流／温度変化等により、星からの波面に乱れが生じます。

（２）大気の影響を考慮した精度(Optical quality considering atmospheric effect)
　　（大気系＋望遠鏡系）のトータルシステムとしての波面収差は、大気の影響による波面収差と対物レンズ
   による波面収差の２つに分けられます。
　　　今、
　　　　RMSAir(D)=口径Dmmの望遠鏡の大気の影響によるRMS波面収差（注）
　　　　RMSlens=対物レンズによるRMS波面収差
　　　とするとき、トータルシステムとしてのRMS波面収差RMSTotal(D)は、どうなるでしょうか。
　　　（注）大気の影響によるRMS波面収差は、望遠鏡の口径が大きいほど増大するので（下図参照）
　　　　　　RMSAirは、望遠鏡の口径Dmmの関数としました。
　　
　　　　　

　　１）確率変数の合成
　　　　Air Turbulenceおよびレンズによる誤差は、各々独立な事象の確率変数X１、X２と考えます。統計論
     によれば、
　　　「確率変数X１、X２が互いに独立でそれらの分布がN(μ１、σ１^2),N(μ2、σ2^2)に従うならば、
       統計量T=X1+X2の分布は、N((μ１+μ2)、(σ１^2+σ2^2))に従う。」ということがわかっています。
　　　　ここで、N(μ、σ^2)とは、平均＝μ、標準偏差＝σの正規分布です。
　　
　　２）トータルシステムとしてのRMS波面収差
　　　　Air Turbulenceを正規分布とするのは異論のあるところですが、あくまでも試算として割り切って
       みます。
　　　　１）の、独立事象での正規分布の合成により、トータルシステムとしてのRMS波面収差は、
　　　　　　　RMSTotal(D)^2＝RMSAir(D)^2＋RMSlens^2
　　　　　　　つまり、
　　　　　　　RMSTotal(D)＝SQRT（RMSAir(D)^2＋RMSlens^2）
　　　　　　　（ここで、SQRTは平方根を意味します。）
　　　　となります。

　　３）算出事例
　　　２）で求めた式により、いくつか例を示します。

　　　（例１）口径D1mmの望遠鏡で、RMSAir(D1)=1/２０λ、RMSlens＝1/１５λの場合
　　　　　　（PーV波面収差＝1/4λ　⇔　RMS波面収差＝1/14λなので、この場合、かろうじてPーV波面
　　　　　　収差＝1/4λを満たす。つまり、ディフラクションリミテッドに一応達しているとします。）
　　　　　　　RMSTotal(D1)＝SQRT(1/20^2+1/15^2)≒1/12λ
　　　　　　　→大気の影響により、PーV波面収差＝1/4λを満たさなくなる。つまり、ディフラクション
　　　　　　　　リミテッドに達しなくなる。
　　
　　　（例２）口径D1mmの望遠鏡で、RMSAir(D1)=1/２０λという大気の条件で、２つの精度の異なる
　　　　　　望遠鏡を比較します。
　　　　　　　１台目は、RMSlens＝1/１５λの精度の望遠鏡（通常程度の精度）
　　　　　　　２台目は、RMSlens＝1/３５λの精度の望遠鏡（高精度望遠鏡）
　　　　　　　このとき、各々の望遠鏡の精度はどうなるでしょうか？
　　　　　　　＜１台目＞
　　　　　　　　RMSTotal(D1)＝SQRT(1/20^2+1/15^2)≒1/12λ
　　　　　　　＜２台目＞
　　　　　　　　RMSTotal(D1)＝SQRT(1/20^2+1/35^2)≒1/17λ
　　　　　　　→2台目の望遠鏡は、PーV波面収差＝1/4λをクリアしています。ところが、１台目はクリア
　　　　　　　　できていない。
　　　　　　　　つまり、望遠鏡の精度の差は、大気の条件が良くないときに出る。
　
　　　（例３）レンズの精度は同じだが口径が異なる望遠鏡の比較。
　　　　　　　口径D1mm、D2mm(D1＜D2)の２つの望遠鏡(レンズの精度は同じ)が下記の大気の条件にある
              とします。
　　　　　　　　・口径D1mmの望遠鏡で、RMSAir(D1)=1/２０λ
　　　　　　　　・口径D2mmの望遠鏡で、RMSAir(D2)=1/１５λ
　　　　　　　レンズの精度は、どちらも
　　　　　　　　・RMSlens＝1/３５λの精度の望遠鏡（高精度望遠鏡）
　　　　　　　このとき、各々の望遠鏡の精度はどうなるでしょうか？
　　　　　　　＜１台目＞
　　　　　　　　RMSTotal(D1)＝SQRT(1/20^2+1/35^2)≒1/17λ
　　　　　　　＜２台目＞
　　　　　　　　RMSTotal(D1)＝SQRT(1/15^2+1/35^2)≒1/9λ
　　　　　　　→１台目の望遠鏡は、PーV波面収差＝1/4λをクリアしています。ところが、２台目はクリア
                 できていない。

（３）補足(Appendix)
　　上記の件に関連した内容で本に載っていたことです。
　　１）大気による波面の乱れを数学的に表現するのは、フラクタルが良いということです。フラクタル構成
     の例が載っています。考え方は、2分割法（binomial)に近いと思います。大気の乱れのフラクタル構成
     については、いずれレポートしたいと思います。（Star Testing Astoronomical Telescopes　P１３２）

　　２）星像の乱れる角度とエアリ−ディスクのサイズとの比較により大気の乱れを表す方式。
　　　（High Resolution Astrophotography　P３）


＜参考図書＞
　　　1.統計解析のはなし　石村貞夫著　東京図書
　　　2. Star Testing Astronomical Telescopes,H.R.Suiter ,Willmann-Bell
　　　3. High Resolution Astrophotography,Jean Dragesco, Cambridge