光学精度のこと
望遠鏡のカタログには、レンズや鏡の光学精度として、PーV波面収差、RMS波面収差、ストレールレシオ等
が出てきますが、この意味について少し調べてみました。
(1)波面収差
まず、波面とは?ということからみて見ます。光は波なので、星からの光は無限遠点から放射される球面
波面としてやって来ます。このイメージは、池に石を投げたとき、石が落ちた所を中心とした同心円として
拡がることに相当します。波の周期のため波長の間隔をおいて同心円が出来ます。ここで、同心円は、同じ
位相の波頭を結んだもの(波底でも良い)です。
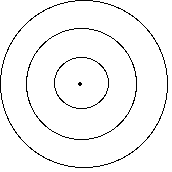
上の図は、同じ拡がりにある波頭を結んだ同心円を示しています。池に拡がる波は2次元ですが、星からの
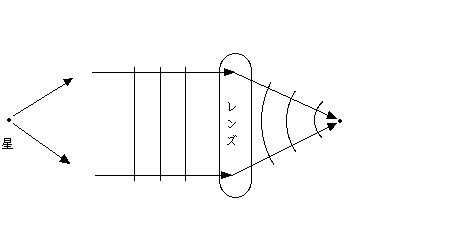
波は3次元なので同心球面波面として拡がります。但し、星は無限遠点にあるとみなすと、同心球面波面は半
径が無限大の球と考えられますので、平行な平面波面としてやって来ます。これがレンズを通過すると、今度
は一点に収束する同心球面波面として進みます。収束する1点を焦点と言います。2次元的にこのイメージを
図示すると、下のようになると思います。但し、レンズの周辺の光はどうなるのかという疑問があります。
→レンズの周辺の光ついて調べてみると、下記のことが書いてありました;
「レンズの端で光が回り込むことにより回折現象が起きます。レンズの縁が光の回折実験のスリットと
同様な役割となっています。望遠鏡による星の回折現象もこれと同じ原理です。」
波面収差とは、レンズを通過した同心球面波面の乱れのことです。上図のように焦点に収束する同心球面波面
を理想波面といいます。これに対して実際の波面は理想波面と較べて偏差があります(くだけて言えば凸凹して
いるということ)。今後は、簡単のため、同心球面波面とは言わずに単に波面と呼ぶことにします。
ここまでくるとようやくPーV波面収差のところへ行き着きます。
(2)PーV波面収差
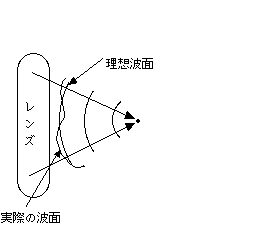
上図のように、レンズを通過した実際の波面は、理想波面に較べて偏差があります。これは、実際の波面が理想
波面に対して波打っているのでずれのピークと谷があります。このピークと谷の差、つまり理想波面とのずれの最
大値をPeakから Valleyまでの偏差(山から谷までの偏差)といい、PーV波面収差と言います。PーV波面収差を
トータル波面収差とも言います。
(3)RMS波面収差
それでは、次によく出てくるRMS波面収差についてみて見ます。RMSとは、root mean square(平均自乗
平方根)の略ですが、これでは何のことかわからないので、図で説明します。
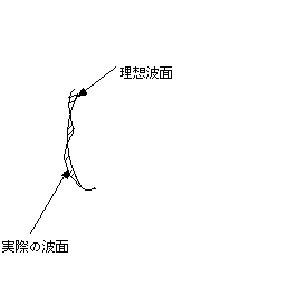
上図のように、実際の波面と理想波面には多かれ少なかれ至る所で偏差があります(完全無欠のレンズでない
限り)。この偏差を表現する方法としては、統計でよく使われる分散及び標準偏差があります。
実際の波面と理想波面には至る所偏差があるといいましたが、波面上のある点Xでの偏差は、
(Xでの実際の波面ーXでの理想波面)
で表わされます。
この偏差の平均Mは、
M=Σ(Xでの実際の波面ーXでの理想波面)/(測定点Xの個数)
です。(Σは、波面の測定点Xについて考えます。)
ここまで準備して、分散と標準偏差を説明します。
1)分散
分散S^2(Sの2乗をS^2で表わします。)とは、実際の波面と偏差の平均Mとの差の自乗平均のことです。
自乗とは2乗のことですが自分と同じものを掛けるので特に自乗といいます。式で表わせば、
S^2=(Σ((Xでの実際の波面ーM)^2))/(測定点Xの個数)
分散は、平均からのデータの散らばり具合を示す統計量です。何故、2乗するかということについては、
数学的に処理しやすいからです。(2乗せずに絶対値をとればと思いがちですが、絶対値は処理しにくい
ものです。絶対値のある関数は、微分/積分が扱いにくいなどの理由によります。)
2)標準偏差
分散の平方根を標準偏差といいます。実は、RMSとは、この標準偏差のことです。つまり、RMS波面収差
の意味は、理想波面と実際の波面の標準偏差です。
では次に、PーV波面収差とRMS波面収差との関係についてみて見ます。ここの部分の考察は、統計理論からの
私見ですので参考程度にして下さい。
(4)PーV波面収差とRMS波面収差の関連
一般に、
PーV波面収差=1/4λ ⇔ RMS波面収差=1/14λ
の対応があると言われます。(Star Testing Astoronomical Telescopes P7)
近似的には、PーV波面収差≒3×RMS波面収差
3というのはかなりおおざっぱですが、この関係を統計的に表現すると、
データの誤差は、標準偏差の3倍以内にほとんどある。
これは、統計的にはかなり妥当な主張だと思います。
以下、図を使って説明します。
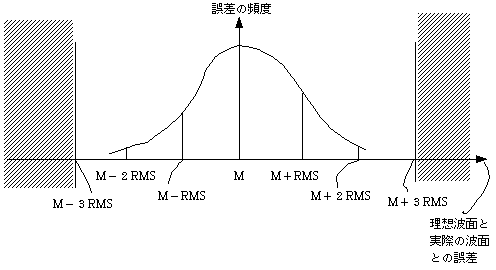
今、理想波面と実際の波面との偏差の平均をMとし、誤差の値を横軸、誤差の頻度を縦軸にとりグラフを書いて、
上の図のようになったとします。偏差の平均付近が頻度が多く、平均からはなれるほど頻度は少なくなるという、
いわゆる正規分布に近いと考えると、(鏡面研摩による製作誤差の分布がどういう分布に近いかによりますが、
ここでは一応、正規分布に近いとしておきます。)誤差の範囲は、標準偏差RMSの3倍以内に殆ど入っていると
いえます。つまり誤差は、上の図の3RMSより大きい斜線部分には殆どない。
→したがって、PーV波面収差は、M−3RMSとM+3RMSの範囲に殆どあるので、
PーV波面収差≒3×RMS波面収差
の関係が成立します。
(5)1/4 波長 レイレ−・トレランス
上記で、PーV波面収差とRMS波面収差の意味およびその関係について述べましたが、次は、回折限界との関係
です。これについては、一般的に次のことが言われています。
「PーV波面収差がイエローグリーンライト(550nm)の波長の1/4を超えるとその光学系の品質が低下する。
→PーV波面収差=λ/4が光学系の品質の許容限度として使用される。これを、1/4 波長の品質(レイレ−・
トレランス)という。」
(注)トレランス:許容限度
(6)鏡面精度
鏡面精度では、よくλ/8が出て来ますが、今までの話しとの関係は次のようになります。今までは、波面に注目
しましたが、鏡面は、入ってくる波面と反射する波面の2つについてPーV波面収差を満たさなければなりません。
つまり、鏡面は、λ/4の2倍の精度=λ/8が要求されます。
(7)精度についてまとめると、
PーV波面収差=λ/4 ⇔ 鏡面精度=λ/8 ⇔ RMS波面収差=λ/14
単に、λ/nではわからないので波面収差なのか、鏡面精度なのか、PーVなのか、RMSなのかが必要です。
(8)ストレールレシオ
光学的品質の評価によく使われるものとして、ストレールレシオがあります。これは、ディフラクションリング
のセントラルスポット(最も明るい部分)に集まる光の強度と、無収差の光学系のセントラルスポットに集まる光
の強度との比のことです。一般に、ストレールレシオ=0.8の値に達した場合、その光学系は、回折のみの制限
をうける(ディフラクションリミテッドに達する)。これは、λ/4レイレ−トレランスに相当します。
(9)RMS波面収差とストレールレシオの関係
ストレールレシオは、RMS波面収差から近似的に次の式により求められます。
(Star Testing Astoronomical Telescopes P.238 より)
ストレールレシオ≒1-(2π×RMS波面収差)^2
(10)例
1)telescope−reviewサイトのスターマスターの高精度ミラーは、
RMS wavefront error:1/74
(Peak to Valley Wavefront error:1/29.6)
Strehl Ratio:0.993
となっています。
→RMS波面収差=λ/74ならば、(8)の式より確かに
ストレールレシオ=1-(2π×1/74)^2=0.993
となります。この値を見ると恐るべき高精度と言えます。
<参考図書>
1. Star Testing Astronomical Telescopes,H.R.Suiter ,Willmann-Bell
2. 統計解析のはなし 石村貞夫著 東京図書
戻る。