星見雑記帳 2019年1月〜
12月22日(日)
・今年もあと9日ですが、今年を振り返ると天気に恵まれない年でした。
同好会の観望会の結果は、29回実施して晴れたのは12回しか
ありませんでした。曇りのときの対策が必要です。
・APQ100/640は25年間主力の望遠鏡でしたが、もう十分使ったので
新機材購入のためツァイスのアイピース類と一緒に手放しました。
新しい望遠鏡が来るまで望遠鏡はクエスター3.5のみです。
これによりHPのタイトルから「4インチ屈折の世界」を削除しました。
9月29(日)
(1)久々に二重星の本が出版されたので入手しました;
Bob Argyle他著 An Anthology of Visual Double Stars
サイズは22cm×27.5cmと大きな本です。
この本の特徴は、175個の主要な二重星について
下記の情報が見開きで載っています;
・Physical parameter:基本データ
・History:最初に発見されてからの歴史)
・Finding Chart:二重星の案内星図
・Orbit:軌道図
・The Modern Era:最近の情報
・Observing:観測情報
・Measures:発見された頃と最近の測定
→本の紹介と見開きのイメージは
Cloudy NightsのDouble Star Observingの
An Anthology of Visual Double Stars
に載っています。

(2)車のダウンサイジング
犬も亡くなり今の車は二人だけで乗るには大きすぎるので、
現行のゴルフバリアントからワーゲンの最小サイズの車 UP! に
替えました(9/27に納車したばかりです)
(3)10月の観望会予定
・10月5日(土) すばる天文同好会の定例観望会
・10月12日〜14日 星の村スターライトフェスティバル(田村市)
・10月26日〜27日 第二回DeepSky観望会in 鬼が城(いわき市)
9月5日(木)
Cloudy NightsにAstro-Physica 10" Mak-Cassの話題がありますが、
これを読むと最近ようやく製品が提供されたようです。
驚くのはその納期の長さです。1999年に注文リストに登録された人が
今年の5月に完成品を手にしたということですから納期20年です。
Astro-Physicsの納期の長さは有名ですが、これは異常な長さです。
Questarも受注生産なので時間がかかりますが、Questarのフォーラムで
"Patience is your friend. A Questar is a lifetime scope,
and delivery is lightening fast compared to an Astro-Physics telescope."
と言われるようにAstro-Physics較べたら大したことありません。
8月30日(金)
天体には点光源と面光源があり、分解能もそれに対応したものを
考える必要があります。
(例)ドーズのリミットは2つの点光源を望遠鏡で見たときの分解能。
一方、広がりのある天体の分解能はコントラストの変化で見ます。
→この資料を参照。
分解能の話でこれらを混同しているような議論をしてないでしょうか
(面光源の分解能をドーズリミットで議論など)。
→そのような混同を防ぐにはMTFがどのように導かれるかというような
仕組みを理解する必要があると思います。同好会のMTFの勉強会の
目的はここにありました。
8月28日(水)
先週土曜日はスバル天文同好会で勉強会を実施しました。
内容は下記でした。
日時 : 8月24日13:00〜15:00
場所 ; 高萩市中央公民館2階小会議
内容及び説明者
(1)メシエカタログ原典紹介・・・・・ 舟越
メシエカタログにどんなことが書かれているか等、古典の紹介です。
(2)MTFの話 ・・・・・ 舟越
MTFはカメラレンズの評価でも使われる評価指標です。MTFがどんな
ものか、その考え方を紹介する内容です。
配布資料は下記;

勉強会の結果は
すばる天文同好会のホームページ
を参照下さい。
8月19日(月) (8/28追記)
夏の観望会の実施状況→今年の天気は散々でした;
茨城県北部の夏は、昼間天気が良くても夕方から雲や霧が出てきて
あっという間に曇ってしまう日が多いです。7月、8月のこれまでの
地域での観望会の状況は下記のようにまともに晴れた日がありません;
・7月19日:XX少年の家での観望会→×(天候不良で中止)
・7月20日:XX小学校での観望会→×(天候不良で中止)
・7月27日:XX小学校での観望会→×(天候不良で中止)
・8月1日:XX科学館での観望会→△(雲間から土星、木星が見えた)
・8月9日:XX科学館での観望会→×に近い△(短時間だけ雲間から木星、土星、月)
・8月16日:××グランピング会場での観望会→△(雲間からうす雲を通した土星、木星、月)
・8月17日:XXの里での観望会→×(昼は天気が良かったが夕方から空一面の雲)
・8月21日:××科学館での観望会→×(天候不良で中止)
・8月22日:××小学校での観望会→×(天候不良で中止)
・8月23日:××科学館での観望会→×(天候不良で中止)
・8月25日:××科学館での観望会→×(天候不良で中止)
・8月26日:XX科学館での観望会→○(土星、木星が良く見えた)
→12回実施中、中止が7回、まともに見えたのは1回位でした。
8月5日(月)
8/2〜8/4は乗鞍高原での観望会に参加しました。
電車とバスで行ったので荷物は下のベンチの上のようになりました。
(クエスターを入れたバック、サイトロンのカーボン三脚、クエスターを
載せる木製のテーブル、小型のキャリーバック)

(新島々のバスターミナルのベンチにて)

(宿の前から眺めた乗鞍:昼間は良く晴れています)
昼は天気が良かったのですが夕方以降は雲が出てきて、星が見えても
晴れ間が長続きせず雲がそらを覆うような天候でした。夏の山の気候は
変わりやすいです。
7月15日(月)
7/12の雑記帳の補足としてデカルトの卵形について説明します;
図のように、屈折率n1 の空間の点Sからの光が屈折率n2の空間において
点Pに集まる(すなわち、Pは焦点)とすると、屈折率が変化する境界面の
形状はどうなるでしょうか?
→境界面が球面ならば球面収差が発生して点Pという1点には集まりません。
この問題を解くためには、「2点を結ぶ道で経過時間(光路長)を最小とする道
が実際に光線がたどる軌跡を与える」というフェルマーの定理を使って、
境界面の点をQとするとき
SQ*n1 + QP *n2= 一定
という条件から求めることができます。このようにして求まる境界面が
図の下のようなデカルトの卵形(Cartesian oval)面です。
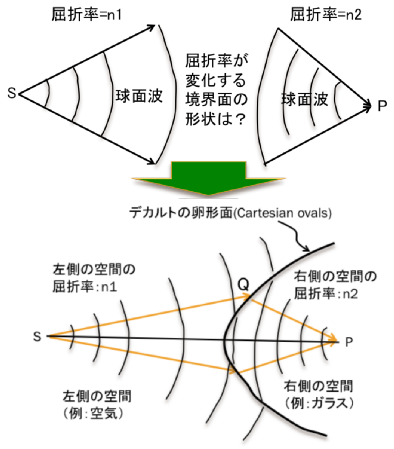
デカルトの卵形問題はSからの波面、Pへの波面が共に「球面波」でしたが、
一般化されたデカルトの卵形問題は、「与えられた入力波面に対して
他の与えられた出力波面に変換する屈折面(refractive surface)を
求めることである」とあるように、球面波でない任意の波です。
(追記:7/16)
一般化されたデカルトの卵形問題について
Roland Winston他 著、Nonimaging Optics という本のP.185に下記記述があり
ましたのでその部分を引用します;
"It is well known that a single refractive or reflective surface can sharply
image a bundle of rays into a point if no more than one rays passes through
each point of the surface. In general, a single surface can transform a given
bundle of rays into another predetermined one if there is no more than one
ray crossing each point of this surface. We call these surfaces generalized
Cartesian ovals. The problem of determining a generalized Cartesian can be
solved simply requiring the constant path length between the incident and
the emergent wavefront. A Cartesian oval problem is that of finding an optical
surface that couples two spherical wave fronts (including the case of infinite
radius sphere ? that is , the plane). We call it a generalized Cartesian oval problem
when we don't require the wave fronts to be spherical."
"単一の屈折面(又は反射面)は、その面の各点でその点を通過する(又は反射する)
光線が1つしかないならば、光束を1点に写すことができる。一般に、単一の表面は
この表面の各点で1つ以上の光線が交わることがなければ、与えられた光束を予め
与えられた他の光束に変換することができる。このような表面を「一般化されたデカルト
の卵形」と呼ぶ。一般化されたデカルトの卵形を決定する問題は、その表面から入力と
出力の波面までのパスの長さを一定とすることにより解決することができる。(通常の)
デカルトの卵形問題は、(無限の半径の球面、すなわち平面を含む)2つの球面波面の
組に対する光学面を求める問題である。波面が球面でないときを一般化されたデカルト
の卵形問題と呼ぶ。"
7月12日(金)
最近、ツイッターなどで
「2000年以上にわたって科学者を悩ませた「レンズの収差問題」がついに解決される」
という記事が話題になっていますが、その論文は下記の2つです;
(1)General formula for bi-aspheric singlet lens design freeof spherical aberration
(2)General formula to design a freeform singlet free of spherical aberration and astigmatism
この論文(2)の序文を読みましたのでその訳を下記に示します;
(キーワードは、
「自由形状光学(Freeform optics)」、
イタリアの数学者レビ・チビタが1900年に「Malus-Dupinの定理の補遺」という
論文で示した、
「一般化されたデカルトの卵形問題( generalized Cartesian oval problem)」
などです。
論文(2)のタイトル:球面収差と非点収差のない自由形状単レンズを設計するための一般式
1.序文
自由形状光学(Freeform optics)には、光が伝わる軸に関して並進対称性や回転対称性
のない表面を少なくとも一つ持つ光学エレメントの設計がある。最近、この話題は光学の
コミュニティで評判になってきた。その理由の一つには新しいコンピュータ技術の急速な
発展とその潜在的応用の出現である。
一般に、自由形状のエレメントの設計は、力ずくの最適化技術(brute-force optimization
techniques)と理論的近似手法を組み合わせていて、種々の結果や特定のケースの有効性
を証明する方法論を導く[1,2]。例えば、Forbes [3-6]は非回転対称システムに対する特性
多項式の集合に基づく自由形状面を記述している。最近、光学収差をかなり減少させた
自由形状ミラーが研究されている。自由形状光学の収差理論は数値最適化のスキーマを
適用することjにより[9-12]で研究されてきた。最近になって、同時多重表面手法(simultaneous
multiple surfaces method)により、一般化されたデカルトの卵形に基づく数値的アプローチ
を採用したシンメトリックなケースが報告されている[13-18]。一般化されたデカルトの卵形
問題は、解析的な閉形式(注)の式を与えることなしに1900年にレビ・チビタにより最初に
考えられた[19]。
(注)閉形式(closed-form)とは?
→加減乗除や初等関数の合成関数による解の表し方
一般化されたデカルトの卵形問題は、与えられた入力波面に対して他の与えられた出力波面
に変換する屈折面(refractive surface)を求めることである。
この論文では、波面の一つが自由形状であり他の一つが球面のケースを扱う。自由形状の
波面はレンズの第一面により生成され、球面波面はレンズの第二面により生成される。
さらに、我々の研究[20, 21]の継続として、球面収差と非点収差のない自由形状単レンズの
設計のための「閉形式の式」を導入する。
この式は、入力波面の任意の自由形状の式を与えたとき、その波面により生じる球面収差と
非点収差を補正するように出力の波面の正確な解析的式を与える。その式の導出は、
標準的な幾何光学の近似の下で、変分フェルマーの原理(variational Fermat principle)の形式的
適用に解析的に(完全に)基づく。式の導出過程では、数値最適戦略という、方法論に依存しない
設計を適用する。また、これまで光学設計では使われることがなかった非常に洗練された入力
関数を使用して、いくつかの代表的な設計の例を示すことにより、式の応用性とロバスト性を
提示する。
我々の知る限りでは、この正確な式は光学の文献にこれまで報告されていない。
論文(2)の序文は以上です。
また、紹介の記事を読むと、
「また、ゴンザレス氏やチャパッロ氏ら研究チームは、General formula to design a freeform
singlet free of spherical aberration and astigmatismという論文も発表し、1900年に定式化された
Levi-Civita問題も解決したと報じられています。」の意味も分かります。
すなわち、Levi-Civita問題=一般化されたデカルトの卵形問題であり、この論文では
「自由形状の波面はレンズの第一面により生成され、球面波面はレンズの第二面により
生成される。」ということで実現しています。
7月7日(日)
天文ガイド8月号のBOOK GUIDEを見たら
6月中旬までに届いた主な天文書の中に
「宇宙と宇宙をつなぐ数学 加藤文元著 角川書店(専門書です)」
というのが載っていましたが、これは数学書で天文との関係はなさそうです。
タイトルの宇宙とは、数学の舞台(特定の数学的領域全体を指す言葉)のことであり、
星々が輝いている物理学の宇宙を指しているわけではありません。
「宇宙と宇宙をつなぐ」とは、複数の数学の舞台どうしの関係、すなわち「宇宙際(うちゅうさい)」
のことです。これは国と国の関係を国際と呼ぶのに対応します。
そして、「宇宙と宇宙をつなぐ数学」とは、数学の難問であるABC予想の解決
のために望月教授が打ち立てた宇宙際タイヒミュラー理論(IUT理論)(注)のことです。
(注)Inter-universal Teichmuller theory
この本は数学者でも理解できる人が世界に10人くらいしかいないような超難関な
IUT理論を数式を使わずに説明した本として数学に関心のある人向けの本です。
5月29日(水)
Airyの1834年の論文"On the Diffraction of an Objective-glass with Aperture"
の解説書(約30頁)を作成しました。エアリーの論文は殆ど数式で図はないので、
図を中心に説明を付け加えました。また、予備知識として波の三角関数表現が
必要なので論文を読むための準備という項を設けました。今から180年前の僅か
9ページの論文ですが、円形開口の回折の数学的定式化に初めて成功したものです。
ここで使われている数学は、現代では高校で学ぶ程度の三角関数と積分のみです。

5月23日(木)
・Neil English著 Chronicling the Golden Age of Astronomy
A History of Visual Observing from Harriot to Moore

を入手しました。660頁の分厚い本ですが過去の有名な眼視観測者の興味ある
話が載っています。特に、W. Herschelについては詳しく書かれています。
N. English氏は、Classic Telescopes: A Guide to Collecting and Using Telescopes
of Yesteryear の著者でもあります。
・5/11, 12は、八ヶ岳の麓の小淵沢で行われた「望遠鏡オフ会」に行ってきました。
この会ではツァイス望遠鏡が主体です。私はAPQ100/640とクエスター3.5を持って
行ったのですが、APQは車から出さずクエスターで春から夏の二重星やメシエ天体
を見ました。下の写真は帰りに寄った牧場から見た八ヶ岳です。

5月10日(金)
・GWはどこも混むので近場しか出かけず、AiryとRayleighの光学に関する論文を
読んでいました。
Airyの方は、1834年の"On the Diffraction of an Objective-glass with Aperture"
です。これは円形開口の回折像を数式により初めて求めた有名な論文です。
その手法は、現代のような複素表現やベッセル関数は使わず、回折光の積分
( (1-w2)1/2*cos nw の積分)において、cos nwをテイラー展開して
x2*(1-w2)1/2、x4*(1-w2)1/2、x6*(1-w2)1/2
という3つの積分計算をすることに帰着させ、答えを求めています。
これは非常に直接的で現在の解法よりも非常に分かり易いものでした。
Rayleigtの方は、1879年の"Investigations in Optics, with special reference
to the spectroscope"のsection1と2です。これは無遮蔽と中央遮蔽の分解能
の違いなど非常に分かり易い内容でした。
・GWに混むので有名な「ひたち海浜公園」はGW前の平日に行きました。
ネモフィラの丘は平日でもかなりの人でした。

4月15日(月)
◆五藤光学のファイラーマイクロメーター
ネットで下記を見つけました。かなり古いもののようですが、方位角も付いて
います。かなり珍品です。
http://kazdon.tokyo/homepage_nakahara/085_kizai/S-FMM/S-FMM.html
4月14日(日)
昨日と今日は第11回星空案内人の集い(山形県最上町)に参加してきました。
参加者は約60名。初日は2つの講演会と天体観望会、及び懇親会があり、
二日目は午前中までで活動・研究報告がありました。この中で私はファイラー
マイクロメーターについて紹介しました。
会場は、大堀温泉 保養センターもがみ。屋上からは残雪の山々が目の前に
拡がります(天気も良く観望日和でした)。

保養センターの屋上ドームには、アストロ光学のD=151mm, f=1500mmのED屈折
望遠鏡があり、この日は月面を見ました。

(4/14 追記)「第1回Deep Sky 観望会 in 鬼ケ城」の詳細レポート;
「楽しみ2倍?【第1回 Deep Sky 観望会 in 鬼ヶ城】詳報!」という
井上さんのブログに詳しく紹介されています。
4月12日(金)
◆先週土日は「第1回Deep Sky 観望会 in 鬼ケ城」に参加しました。
鬼ケ城はかなり山の中で途中、狭い道があります。参加は福島、茨城、栃木、
東京から全員で14名でした。
観望会場は遠くの山並みが低く見え南側の見晴しが非常に良いです。
写真は日没前で、このときは良く晴れていました。しかし、暗くなると南東から
雲が拡がり、透明度も悪く、しだいにうす雲の合間での観望となりました。
ここは遠くまで周りに明かりはなく、晴れて透明度が良ければ素晴らしい
観望地だと思いました。
スピカが昇ってきたころには雲が空一面を覆ってきたので観望は終了し、
宿の大広間で交流会となりました。ここでは、双眼望遠鏡の正立ミラーの
紹介、また、翌日には朝食後にMasuyama eyeiecesラインナップの紹介が
ありました。次回開催されればまた参加したいと思います。


◆高萩市さくら宇宙公園の桜
すばる天文同好会の定例観望会を実施している場所ですが桜が咲いているので
写真を撮りました(4月9日)。広大な敷地に電波望遠鏡が二基あります。



4月4日(木)
クエスターを使って大犬座の二重星(冬のアルビレオ)をAstrometoric eyepiece
で測定しました(離角のみ)。倍率は、1300/12=108倍
このときの離角は、1.5目盛でした。冬のアルビレオの離角は 26"9なので
Astrometoric eyepieceの1目盛=17.4秒角 となりました。
ファイラーマイクロメーターに較べると精度は1/10程度です。
精度を上げるには、もっと倍率を上げる必要があります(300倍で1目盛=5.7秒角)。
4月2日(火)
Meadの12mm illminated Reticle Astrometric Eyepiece が届きました。
天体のサイズや二重星の離角、位置角などを簡易に測定するための
アイピースです。アメリカのAstronomicsから購入しました。
価格は、本体が79.99ドル、送料が24.50ドルでした。
BaaderのMicro Guide Eyepieceに比べると1/3位の価格です。

アイピースを覗くと(一部しか写っていませんが)下記のようなスケールが
見えます。実際測定するときは暗視野照明でスケールは赤く照らされます。

3月19日(火)
・APQ100/1000の再来か?
Cloudy Nightsに
Astro Optik Manufaktur FLT 105 / 1000
の話題が載っています。これを読むと、
「The design was calculated by Dr. Jurgen Pudenz (former working at Zeiss, now retired) and the lenses are handmade by Peter Grose - both was deeply involved in the production of the exceptional Zeiss APQ scopes years before. Now these scopes have a worthy successor - the FLT 105/1000 - where FLT stands for "Fluorit Triplet". The scope uses the same layout as the original APQ´s - an oil filled triplet with a fluorit lens as center element.」
とあるように、レンズの設計はAPQの設計者の一人であるDr. Pudenz、レンズ構成もAPQと同じです。
3月12日(火)
◆クエスターを使って大犬座の二重星(冬のアルビレオ)をファイラーマイクロメーター
で測定しました。測定手順は下記に従いました;
Filar micrometerの使用法
冬のアルビレオの測定結果は下記でした;
North point: -a=-16°
b=301°
従って、位置角= b+90°-(-a) = 301°+90°+16°
=417°= 360°+ 57°= 57°
星座ガイドブック(秋冬編)を見ると、
冬のアルビレオの位置角は、55°
→2°の差異がありますが、初めての測定で慣れていない
のに加えて1回しか測定してないことを考えると妥当な値です。
離角の方は、18目盛でした。冬のアルビレオの離角は
上の本では、26"9なので
マイクロメーターの1目盛=1.45秒角
となりました。
◆4月は下記に参加予定です;
・第1回Deep Sky観望会 in 鬼ヶ城(4/6,7)
・第11回星空案内人の集い(4/13, 14 山形県最上町)
2月15日(金)
現在、主に使用しているアイピースなど。左から、
・QUESTAR BRANDON 12mm, 24mm
・(Zeiss) JENA Monocentric 10mm
・Zeiss A-4, A-25
・Zeiss W-31S (31mm Widefield Erfle)
・Zeiss 2×Barlow
・Zeiss diagonal

モノセントリックを上から見ると、JENA Mon Okular f=10mm と書かれています;

これ以外には、テレビューのアイピースがあります。
2月12日(火)
私のレポートに
「結像システムと畳み込み」を載せました。
2月5日(火)
昨日は気温が上昇し、NHKのニュースには花粉の話題が出ていました。花粉の季節に
なると望遠鏡のレンズにも付着するので花粉の季節にはレンズの汚れ防止として保護
フィルターを付けることにしています;
APQの場合は112mmのケンコーフィルターを対物キャップに付けています.。
フィルターが付けられる対物キャップの製作はY製作所に依頼しました;


クエスターの場合は筒先にフィルターネジが切ってあるので
ここにケンコーフィルターを付けています;

2月4日(月)
先週の土曜日はすばる天文同好会の定例観望会でした。参加人数は4名と少なかった
のですが天気は晴れで月もなく好条件でした。下の写真は定例観望会の場所(茨城県
高萩市のさくら宇宙公園)の夕暮れ。中央に見えるのは電波天文台のパラボラアンテナ。

今回は東京からH氏がAPQ130/1000で参加されたので、星団などをAPQ100/640,
クエスター3.5と見比べました。プレアデスや二重星団を見て感じたことは、クエスター
の視野の背景の暗さが際立っていることでした。そのため星の輝きが綺麗に見えます。
APQは口径が大きいので空の明るさを拾っているのかもしれませんが、それだけでは
ないような気もします。クエスターの内部の遮光はどうなっているのでしょうか?
cloudy nightsに次のような内部構造を示したものがあります;
Inside Questar
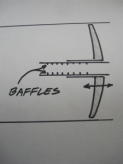
これを見ると、鏡筒の内径は主鏡と同じサイズでここには遮光環はありませんが、
バッフルチューブ内にはコイル・スプリングがあり、これが遮光環として機能して
いるようです;The spring inside the baffle tube serves as a series of baffle rings.
バッフルチューブ内のイメージは下のSecondary Baffleの中に次の図が描かれて
います;
Cloudy nightsのこちらの内容も参考になります;
Secondary Baffle
ここには、マクストフの球面のコレクターのR2面にある副鏡が手磨きの非球面
であることと、反対側でそれを覆うブラックスポットが非球面の副鏡よりわずかに
大きくなっていることが説明されています。これも遮光に役立っていると思います。
以上の遮光によりクエスターは昼間の景色でも非常にコントラストの良い像を
実現しているのでしょう。
1月31日(木)
五藤光学の10cmマクストフがヤフーオークションに登場し注目されました。
鏡筒だけで35万と高額で落札されたようです。五藤の10cmマクストフの登場
はcloudy nightsでも話題になっていました;
GOTO Japan 100/1450 Maksutov
五藤の10cmマクストフの説明書を読むと、球面収差補正のため球面主鏡を
裏面鏡にしているなど興味深い記述が載っています、収差図を見ると球面差
がほぼ完璧に補正されていて、他の収差補正も非常良いとのことです。
この説明書の一部を英訳して上記のcloudy nightsに投稿しました。
各収差補正の良さから見るとクエスター3.5と見比べてみたくなりました。
クエスターも球面収差含めて各収差がほぼ完璧に補正されていて、実際
覗いて見ても視野の周辺までピンポイントな星像です。クエスターの場合は
副鏡を非球面にしていることでこれを実現しているようです。
1月29日(火)
・先週の水曜日は近くの小学校での観望会でした。
クエスターで導入したのはプレアデスやオリオン星雲、ふたご座の
カストルでした。プレアデスは最初にクエスターのファインダーで、
次に拡大して見てもらいました。このとき一瞬で像が変わるので
不思議に思う子もいました。覗いた星の位置の説明はクエスターの
フードの星座を使用しました。アイピースから目を離すと、すぐ近くに
星座が描かれているので星の位置を説明するのに非常に便利です。
プレアデスはブランドン24mmでは全体が入らないのでテレビューの
プルーセル32mmを使用。視野周辺までピンポイントの星像が真っ黒な
背景に輝き非常に綺麗でした。星々の輝きの美しさが伝わったようでした。
小学校の観望会にはクエスターで十分なように思いました。
・最近入手した本;
アメリカのアマゾンから「Integrated Modeling of Telescopes」を入手。
これは、天体望遠鏡システムの光学的あるいは機構的なモデリングを
扱った本です。フーリエ変換による光学的モデリングや大望遠鏡の
波面制御システム(Active optics)など幅広い範囲を網羅しています。

・畳み込みの説明図
畳み込み計算について少し調べました。天体望遠鏡で細かい模様を
見るとなぜコントラストが低下するのかその理由が分かります。
離散的な光度分布を天体望遠鏡で見たときの説明図です。
裾の広い回折像が重なることによりコントラストが低下します;
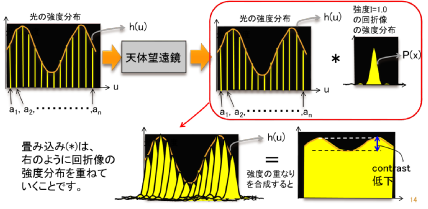
連続的な光度分布の場合は次のように「畳み込み積分」になります;

畳み込み積分の計算は面倒なので、通常はフーリエ変換を
行います。これにより畳み込みは通常の掛け算になります。

12月22日(日)
・今年もあと9日ですが、今年を振り返ると天気に恵まれない年でした。
同好会の観望会の結果は、29回実施して晴れたのは12回しか
ありませんでした。曇りのときの対策が必要です。
・APQ100/640は25年間主力の望遠鏡でしたが、もう十分使ったので
新機材購入のためツァイスのアイピース類と一緒に手放しました。
新しい望遠鏡が来るまで望遠鏡はクエスター3.5のみです。
これによりHPのタイトルから「4インチ屈折の世界」を削除しました。
9月29(日)
(1)久々に二重星の本が出版されたので入手しました;
Bob Argyle他著 An Anthology of Visual Double Stars
サイズは22cm×27.5cmと大きな本です。
この本の特徴は、175個の主要な二重星について
下記の情報が見開きで載っています;
・Physical parameter:基本データ
・History:最初に発見されてからの歴史)
・Finding Chart:二重星の案内星図
・Orbit:軌道図
・The Modern Era:最近の情報
・Observing:観測情報
・Measures:発見された頃と最近の測定
→本の紹介と見開きのイメージは
Cloudy NightsのDouble Star Observingの
An Anthology of Visual Double Stars
に載っています。

(2)車のダウンサイジング
犬も亡くなり今の車は二人だけで乗るには大きすぎるので、
現行のゴルフバリアントからワーゲンの最小サイズの車 UP! に
替えました(9/27に納車したばかりです)
(3)10月の観望会予定
・10月5日(土) すばる天文同好会の定例観望会
・10月12日〜14日 星の村スターライトフェスティバル(田村市)
・10月26日〜27日 第二回DeepSky観望会in 鬼が城(いわき市)
9月5日(木)
Cloudy NightsにAstro-Physica 10" Mak-Cassの話題がありますが、
これを読むと最近ようやく製品が提供されたようです。
驚くのはその納期の長さです。1999年に注文リストに登録された人が
今年の5月に完成品を手にしたということですから納期20年です。
Astro-Physicsの納期の長さは有名ですが、これは異常な長さです。
Questarも受注生産なので時間がかかりますが、Questarのフォーラムで
"Patience is your friend. A Questar is a lifetime scope,
and delivery is lightening fast compared to an Astro-Physics telescope."
と言われるようにAstro-Physics較べたら大したことありません。
8月30日(金)
天体には点光源と面光源があり、分解能もそれに対応したものを
考える必要があります。
(例)ドーズのリミットは2つの点光源を望遠鏡で見たときの分解能。
一方、広がりのある天体の分解能はコントラストの変化で見ます。
→この資料を参照。
分解能の話でこれらを混同しているような議論をしてないでしょうか
(面光源の分解能をドーズリミットで議論など)。
→そのような混同を防ぐにはMTFがどのように導かれるかというような
仕組みを理解する必要があると思います。同好会のMTFの勉強会の
目的はここにありました。
8月28日(水)
先週土曜日はスバル天文同好会で勉強会を実施しました。
内容は下記でした。
日時 : 8月24日13:00〜15:00
場所 ; 高萩市中央公民館2階小会議
内容及び説明者
(1)メシエカタログ原典紹介・・・・・ 舟越
メシエカタログにどんなことが書かれているか等、古典の紹介です。
(2)MTFの話 ・・・・・ 舟越
MTFはカメラレンズの評価でも使われる評価指標です。MTFがどんな
ものか、その考え方を紹介する内容です。
配布資料は下記;

勉強会の結果は
すばる天文同好会のホームページ
を参照下さい。
8月19日(月) (8/28追記)
夏の観望会の実施状況→今年の天気は散々でした;
茨城県北部の夏は、昼間天気が良くても夕方から雲や霧が出てきて
あっという間に曇ってしまう日が多いです。7月、8月のこれまでの
地域での観望会の状況は下記のようにまともに晴れた日がありません;
・7月19日:XX少年の家での観望会→×(天候不良で中止)
・7月20日:XX小学校での観望会→×(天候不良で中止)
・7月27日:XX小学校での観望会→×(天候不良で中止)
・8月1日:XX科学館での観望会→△(雲間から土星、木星が見えた)
・8月9日:XX科学館での観望会→×に近い△(短時間だけ雲間から木星、土星、月)
・8月16日:××グランピング会場での観望会→△(雲間からうす雲を通した土星、木星、月)
・8月17日:XXの里での観望会→×(昼は天気が良かったが夕方から空一面の雲)
・8月21日:××科学館での観望会→×(天候不良で中止)
・8月22日:××小学校での観望会→×(天候不良で中止)
・8月23日:××科学館での観望会→×(天候不良で中止)
・8月25日:××科学館での観望会→×(天候不良で中止)
・8月26日:XX科学館での観望会→○(土星、木星が良く見えた)
→12回実施中、中止が7回、まともに見えたのは1回位でした。
8月5日(月)
8/2〜8/4は乗鞍高原での観望会に参加しました。
電車とバスで行ったので荷物は下のベンチの上のようになりました。
(クエスターを入れたバック、サイトロンのカーボン三脚、クエスターを
載せる木製のテーブル、小型のキャリーバック)

(新島々のバスターミナルのベンチにて)

(宿の前から眺めた乗鞍:昼間は良く晴れています)
昼は天気が良かったのですが夕方以降は雲が出てきて、星が見えても
晴れ間が長続きせず雲がそらを覆うような天候でした。夏の山の気候は
変わりやすいです。
7月15日(月)
7/12の雑記帳の補足としてデカルトの卵形について説明します;
図のように、屈折率n1 の空間の点Sからの光が屈折率n2の空間において
点Pに集まる(すなわち、Pは焦点)とすると、屈折率が変化する境界面の
形状はどうなるでしょうか?
→境界面が球面ならば球面収差が発生して点Pという1点には集まりません。
この問題を解くためには、「2点を結ぶ道で経過時間(光路長)を最小とする道
が実際に光線がたどる軌跡を与える」というフェルマーの定理を使って、
境界面の点をQとするとき
SQ*n1 + QP *n2= 一定
という条件から求めることができます。このようにして求まる境界面が
図の下のようなデカルトの卵形(Cartesian oval)面です。

デカルトの卵形問題はSからの波面、Pへの波面が共に「球面波」でしたが、
一般化されたデカルトの卵形問題は、「与えられた入力波面に対して
他の与えられた出力波面に変換する屈折面(refractive surface)を
求めることである」とあるように、球面波でない任意の波です。
(追記:7/16)
一般化されたデカルトの卵形問題について
Roland Winston他 著、Nonimaging Optics という本のP.185に下記記述があり
ましたのでその部分を引用します;
"It is well known that a single refractive or reflective surface can sharply
image a bundle of rays into a point if no more than one rays passes through
each point of the surface. In general, a single surface can transform a given
bundle of rays into another predetermined one if there is no more than one
ray crossing each point of this surface. We call these surfaces generalized
Cartesian ovals. The problem of determining a generalized Cartesian can be
solved simply requiring the constant path length between the incident and
the emergent wavefront. A Cartesian oval problem is that of finding an optical
surface that couples two spherical wave fronts (including the case of infinite
radius sphere ? that is , the plane). We call it a generalized Cartesian oval problem
when we don't require the wave fronts to be spherical."
"単一の屈折面(又は反射面)は、その面の各点でその点を通過する(又は反射する)
光線が1つしかないならば、光束を1点に写すことができる。一般に、単一の表面は
この表面の各点で1つ以上の光線が交わることがなければ、与えられた光束を予め
与えられた他の光束に変換することができる。このような表面を「一般化されたデカルト
の卵形」と呼ぶ。一般化されたデカルトの卵形を決定する問題は、その表面から入力と
出力の波面までのパスの長さを一定とすることにより解決することができる。(通常の)
デカルトの卵形問題は、(無限の半径の球面、すなわち平面を含む)2つの球面波面の
組に対する光学面を求める問題である。波面が球面でないときを一般化されたデカルト
の卵形問題と呼ぶ。"
7月12日(金)
最近、ツイッターなどで
「2000年以上にわたって科学者を悩ませた「レンズの収差問題」がついに解決される」
という記事が話題になっていますが、その論文は下記の2つです;
(1)General formula for bi-aspheric singlet lens design freeof spherical aberration
(2)General formula to design a freeform singlet free of spherical aberration and astigmatism
この論文(2)の序文を読みましたのでその訳を下記に示します;
(キーワードは、
「自由形状光学(Freeform optics)」、
イタリアの数学者レビ・チビタが1900年に「Malus-Dupinの定理の補遺」という
論文で示した、
「一般化されたデカルトの卵形問題( generalized Cartesian oval problem)」
などです。
論文(2)のタイトル:球面収差と非点収差のない自由形状単レンズを設計するための一般式
1.序文
自由形状光学(Freeform optics)には、光が伝わる軸に関して並進対称性や回転対称性
のない表面を少なくとも一つ持つ光学エレメントの設計がある。最近、この話題は光学の
コミュニティで評判になってきた。その理由の一つには新しいコンピュータ技術の急速な
発展とその潜在的応用の出現である。
一般に、自由形状のエレメントの設計は、力ずくの最適化技術(brute-force optimization
techniques)と理論的近似手法を組み合わせていて、種々の結果や特定のケースの有効性
を証明する方法論を導く[1,2]。例えば、Forbes [3-6]は非回転対称システムに対する特性
多項式の集合に基づく自由形状面を記述している。最近、光学収差をかなり減少させた
自由形状ミラーが研究されている。自由形状光学の収差理論は数値最適化のスキーマを
適用することjにより[9-12]で研究されてきた。最近になって、同時多重表面手法(simultaneous
multiple surfaces method)により、一般化されたデカルトの卵形に基づく数値的アプローチ
を採用したシンメトリックなケースが報告されている[13-18]。一般化されたデカルトの卵形
問題は、解析的な閉形式(注)の式を与えることなしに1900年にレビ・チビタにより最初に
考えられた[19]。
(注)閉形式(closed-form)とは?
→加減乗除や初等関数の合成関数による解の表し方
一般化されたデカルトの卵形問題は、与えられた入力波面に対して他の与えられた出力波面
に変換する屈折面(refractive surface)を求めることである。
この論文では、波面の一つが自由形状であり他の一つが球面のケースを扱う。自由形状の
波面はレンズの第一面により生成され、球面波面はレンズの第二面により生成される。
さらに、我々の研究[20, 21]の継続として、球面収差と非点収差のない自由形状単レンズの
設計のための「閉形式の式」を導入する。
この式は、入力波面の任意の自由形状の式を与えたとき、その波面により生じる球面収差と
非点収差を補正するように出力の波面の正確な解析的式を与える。その式の導出は、
標準的な幾何光学の近似の下で、変分フェルマーの原理(variational Fermat principle)の形式的
適用に解析的に(完全に)基づく。式の導出過程では、数値最適戦略という、方法論に依存しない
設計を適用する。また、これまで光学設計では使われることがなかった非常に洗練された入力
関数を使用して、いくつかの代表的な設計の例を示すことにより、式の応用性とロバスト性を
提示する。
我々の知る限りでは、この正確な式は光学の文献にこれまで報告されていない。
論文(2)の序文は以上です。
また、紹介の記事を読むと、
「また、ゴンザレス氏やチャパッロ氏ら研究チームは、General formula to design a freeform
singlet free of spherical aberration and astigmatismという論文も発表し、1900年に定式化された
Levi-Civita問題も解決したと報じられています。」の意味も分かります。
すなわち、Levi-Civita問題=一般化されたデカルトの卵形問題であり、この論文では
「自由形状の波面はレンズの第一面により生成され、球面波面はレンズの第二面により
生成される。」ということで実現しています。
7月7日(日)
天文ガイド8月号のBOOK GUIDEを見たら
6月中旬までに届いた主な天文書の中に
「宇宙と宇宙をつなぐ数学 加藤文元著 角川書店(専門書です)」
というのが載っていましたが、これは数学書で天文との関係はなさそうです。
タイトルの宇宙とは、数学の舞台(特定の数学的領域全体を指す言葉)のことであり、
星々が輝いている物理学の宇宙を指しているわけではありません。
「宇宙と宇宙をつなぐ」とは、複数の数学の舞台どうしの関係、すなわち「宇宙際(うちゅうさい)」
のことです。これは国と国の関係を国際と呼ぶのに対応します。
そして、「宇宙と宇宙をつなぐ数学」とは、数学の難問であるABC予想の解決
のために望月教授が打ち立てた宇宙際タイヒミュラー理論(IUT理論)(注)のことです。
(注)Inter-universal Teichmuller theory
この本は数学者でも理解できる人が世界に10人くらいしかいないような超難関な
IUT理論を数式を使わずに説明した本として数学に関心のある人向けの本です。
5月29日(水)
Airyの1834年の論文"On the Diffraction of an Objective-glass with Aperture"
の解説書(約30頁)を作成しました。エアリーの論文は殆ど数式で図はないので、
図を中心に説明を付け加えました。また、予備知識として波の三角関数表現が
必要なので論文を読むための準備という項を設けました。今から180年前の僅か
9ページの論文ですが、円形開口の回折の数学的定式化に初めて成功したものです。
ここで使われている数学は、現代では高校で学ぶ程度の三角関数と積分のみです。

5月23日(木)
・Neil English著 Chronicling the Golden Age of Astronomy
A History of Visual Observing from Harriot to Moore

を入手しました。660頁の分厚い本ですが過去の有名な眼視観測者の興味ある
話が載っています。特に、W. Herschelについては詳しく書かれています。
N. English氏は、Classic Telescopes: A Guide to Collecting and Using Telescopes
of Yesteryear の著者でもあります。
・5/11, 12は、八ヶ岳の麓の小淵沢で行われた「望遠鏡オフ会」に行ってきました。
この会ではツァイス望遠鏡が主体です。私はAPQ100/640とクエスター3.5を持って
行ったのですが、APQは車から出さずクエスターで春から夏の二重星やメシエ天体
を見ました。下の写真は帰りに寄った牧場から見た八ヶ岳です。

5月10日(金)
・GWはどこも混むので近場しか出かけず、AiryとRayleighの光学に関する論文を
読んでいました。
Airyの方は、1834年の"On the Diffraction of an Objective-glass with Aperture"
です。これは円形開口の回折像を数式により初めて求めた有名な論文です。
その手法は、現代のような複素表現やベッセル関数は使わず、回折光の積分
( (1-w2)1/2*cos nw の積分)において、cos nwをテイラー展開して
x2*(1-w2)1/2、x4*(1-w2)1/2、x6*(1-w2)1/2
という3つの積分計算をすることに帰着させ、答えを求めています。
これは非常に直接的で現在の解法よりも非常に分かり易いものでした。
Rayleigtの方は、1879年の"Investigations in Optics, with special reference
to the spectroscope"のsection1と2です。これは無遮蔽と中央遮蔽の分解能
の違いなど非常に分かり易い内容でした。
・GWに混むので有名な「ひたち海浜公園」はGW前の平日に行きました。
ネモフィラの丘は平日でもかなりの人でした。

4月15日(月)
◆五藤光学のファイラーマイクロメーター
ネットで下記を見つけました。かなり古いもののようですが、方位角も付いて
います。かなり珍品です。
http://kazdon.tokyo/homepage_nakahara/085_kizai/S-FMM/S-FMM.html
4月14日(日)
昨日と今日は第11回星空案内人の集い(山形県最上町)に参加してきました。
参加者は約60名。初日は2つの講演会と天体観望会、及び懇親会があり、
二日目は午前中までで活動・研究報告がありました。この中で私はファイラー
マイクロメーターについて紹介しました。
会場は、大堀温泉 保養センターもがみ。屋上からは残雪の山々が目の前に
拡がります(天気も良く観望日和でした)。

保養センターの屋上ドームには、アストロ光学のD=151mm, f=1500mmのED屈折
望遠鏡があり、この日は月面を見ました。

(4/14 追記)「第1回Deep Sky 観望会 in 鬼ケ城」の詳細レポート;
「楽しみ2倍?【第1回 Deep Sky 観望会 in 鬼ヶ城】詳報!」という
井上さんのブログに詳しく紹介されています。
4月12日(金)
◆先週土日は「第1回Deep Sky 観望会 in 鬼ケ城」に参加しました。
鬼ケ城はかなり山の中で途中、狭い道があります。参加は福島、茨城、栃木、
東京から全員で14名でした。
観望会場は遠くの山並みが低く見え南側の見晴しが非常に良いです。
写真は日没前で、このときは良く晴れていました。しかし、暗くなると南東から
雲が拡がり、透明度も悪く、しだいにうす雲の合間での観望となりました。
ここは遠くまで周りに明かりはなく、晴れて透明度が良ければ素晴らしい
観望地だと思いました。
スピカが昇ってきたころには雲が空一面を覆ってきたので観望は終了し、
宿の大広間で交流会となりました。ここでは、双眼望遠鏡の正立ミラーの
紹介、また、翌日には朝食後にMasuyama eyeiecesラインナップの紹介が
ありました。次回開催されればまた参加したいと思います。


◆高萩市さくら宇宙公園の桜
すばる天文同好会の定例観望会を実施している場所ですが桜が咲いているので
写真を撮りました(4月9日)。広大な敷地に電波望遠鏡が二基あります。



4月4日(木)
クエスターを使って大犬座の二重星(冬のアルビレオ)をAstrometoric eyepiece
で測定しました(離角のみ)。倍率は、1300/12=108倍
このときの離角は、1.5目盛でした。冬のアルビレオの離角は 26"9なので
Astrometoric eyepieceの1目盛=17.4秒角 となりました。
ファイラーマイクロメーターに較べると精度は1/10程度です。
精度を上げるには、もっと倍率を上げる必要があります(300倍で1目盛=5.7秒角)。
4月2日(火)
Meadの12mm illminated Reticle Astrometric Eyepiece が届きました。
天体のサイズや二重星の離角、位置角などを簡易に測定するための
アイピースです。アメリカのAstronomicsから購入しました。
価格は、本体が79.99ドル、送料が24.50ドルでした。
BaaderのMicro Guide Eyepieceに比べると1/3位の価格です。

アイピースを覗くと(一部しか写っていませんが)下記のようなスケールが
見えます。実際測定するときは暗視野照明でスケールは赤く照らされます。

3月19日(火)
・APQ100/1000の再来か?
Cloudy Nightsに
Astro Optik Manufaktur FLT 105 / 1000
の話題が載っています。これを読むと、
「The design was calculated by Dr. Jurgen Pudenz (former working at Zeiss, now retired) and the lenses are handmade by Peter Grose - both was deeply involved in the production of the exceptional Zeiss APQ scopes years before. Now these scopes have a worthy successor - the FLT 105/1000 - where FLT stands for "Fluorit Triplet". The scope uses the same layout as the original APQ´s - an oil filled triplet with a fluorit lens as center element.」
とあるように、レンズの設計はAPQの設計者の一人であるDr. Pudenz、レンズ構成もAPQと同じです。
3月12日(火)
◆クエスターを使って大犬座の二重星(冬のアルビレオ)をファイラーマイクロメーター
で測定しました。測定手順は下記に従いました;
Filar micrometerの使用法
冬のアルビレオの測定結果は下記でした;
North point: -a=-16°
b=301°
従って、位置角= b+90°-(-a) = 301°+90°+16°
=417°= 360°+ 57°= 57°
星座ガイドブック(秋冬編)を見ると、
冬のアルビレオの位置角は、55°
→2°の差異がありますが、初めての測定で慣れていない
のに加えて1回しか測定してないことを考えると妥当な値です。
離角の方は、18目盛でした。冬のアルビレオの離角は
上の本では、26"9なので
マイクロメーターの1目盛=1.45秒角
となりました。
◆4月は下記に参加予定です;
・第1回Deep Sky観望会 in 鬼ヶ城(4/6,7)
・第11回星空案内人の集い(4/13, 14 山形県最上町)
2月15日(金)
現在、主に使用しているアイピースなど。左から、
・QUESTAR BRANDON 12mm, 24mm
・(Zeiss) JENA Monocentric 10mm
・Zeiss A-4, A-25
・Zeiss W-31S (31mm Widefield Erfle)
・Zeiss 2×Barlow
・Zeiss diagonal

モノセントリックを上から見ると、JENA Mon Okular f=10mm と書かれています;

これ以外には、テレビューのアイピースがあります。
2月12日(火)
私のレポートに
「結像システムと畳み込み」を載せました。
2月5日(火)
昨日は気温が上昇し、NHKのニュースには花粉の話題が出ていました。花粉の季節に
なると望遠鏡のレンズにも付着するので花粉の季節にはレンズの汚れ防止として保護
フィルターを付けることにしています;
APQの場合は112mmのケンコーフィルターを対物キャップに付けています.。
フィルターが付けられる対物キャップの製作はY製作所に依頼しました;


クエスターの場合は筒先にフィルターネジが切ってあるので
ここにケンコーフィルターを付けています;

2月4日(月)
先週の土曜日はすばる天文同好会の定例観望会でした。参加人数は4名と少なかった
のですが天気は晴れで月もなく好条件でした。下の写真は定例観望会の場所(茨城県
高萩市のさくら宇宙公園)の夕暮れ。中央に見えるのは電波天文台のパラボラアンテナ。

今回は東京からH氏がAPQ130/1000で参加されたので、星団などをAPQ100/640,
クエスター3.5と見比べました。プレアデスや二重星団を見て感じたことは、クエスター
の視野の背景の暗さが際立っていることでした。そのため星の輝きが綺麗に見えます。
APQは口径が大きいので空の明るさを拾っているのかもしれませんが、それだけでは
ないような気もします。クエスターの内部の遮光はどうなっているのでしょうか?
cloudy nightsに次のような内部構造を示したものがあります;
Inside Questar
これを見ると、鏡筒の内径は主鏡と同じサイズでここには遮光環はありませんが、
バッフルチューブ内にはコイル・スプリングがあり、これが遮光環として機能して
いるようです;The spring inside the baffle tube serves as a series of baffle rings.
バッフルチューブ内のイメージは下のSecondary Baffleの中に次の図が描かれて
います;

Cloudy nightsのこちらの内容も参考になります;
Secondary Baffle
ここには、マクストフの球面のコレクターのR2面にある副鏡が手磨きの非球面
であることと、反対側でそれを覆うブラックスポットが非球面の副鏡よりわずかに
大きくなっていることが説明されています。これも遮光に役立っていると思います。
以上の遮光によりクエスターは昼間の景色でも非常にコントラストの良い像を
実現しているのでしょう。
1月31日(木)
五藤光学の10cmマクストフがヤフーオークションに登場し注目されました。
鏡筒だけで35万と高額で落札されたようです。五藤の10cmマクストフの登場
はcloudy nightsでも話題になっていました;
GOTO Japan 100/1450 Maksutov
五藤の10cmマクストフの説明書を読むと、球面収差補正のため球面主鏡を
裏面鏡にしているなど興味深い記述が載っています、収差図を見ると球面差
がほぼ完璧に補正されていて、他の収差補正も非常良いとのことです。
この説明書の一部を英訳して上記のcloudy nightsに投稿しました。
各収差補正の良さから見るとクエスター3.5と見比べてみたくなりました。
クエスターも球面収差含めて各収差がほぼ完璧に補正されていて、実際
覗いて見ても視野の周辺までピンポイントな星像です。クエスターの場合は
副鏡を非球面にしていることでこれを実現しているようです。
1月29日(火)
・先週の水曜日は近くの小学校での観望会でした。
クエスターで導入したのはプレアデスやオリオン星雲、ふたご座の
カストルでした。プレアデスは最初にクエスターのファインダーで、
次に拡大して見てもらいました。このとき一瞬で像が変わるので
不思議に思う子もいました。覗いた星の位置の説明はクエスターの
フードの星座を使用しました。アイピースから目を離すと、すぐ近くに
星座が描かれているので星の位置を説明するのに非常に便利です。
プレアデスはブランドン24mmでは全体が入らないのでテレビューの
プルーセル32mmを使用。視野周辺までピンポイントの星像が真っ黒な
背景に輝き非常に綺麗でした。星々の輝きの美しさが伝わったようでした。
小学校の観望会にはクエスターで十分なように思いました。
・最近入手した本;
アメリカのアマゾンから「Integrated Modeling of Telescopes」を入手。
これは、天体望遠鏡システムの光学的あるいは機構的なモデリングを
扱った本です。フーリエ変換による光学的モデリングや大望遠鏡の
波面制御システム(Active optics)など幅広い範囲を網羅しています。

・畳み込みの説明図
畳み込み計算について少し調べました。天体望遠鏡で細かい模様を
見るとなぜコントラストが低下するのかその理由が分かります。
離散的な光度分布を天体望遠鏡で見たときの説明図です。
裾の広い回折像が重なることによりコントラストが低下します;

連続的な光度分布の場合は次のように「畳み込み積分」になります;

畳み込み積分の計算は面倒なので、通常はフーリエ変換を
行います。これにより畳み込みは通常の掛け算になります。
