プログラムの抽象解釈紹介
2014年 作成:舟越 和己
1.抽象解釈とは
現実のプログラムは変数や状態数が非常に大きいことなどがあり、その解析は非常に困難です。抽象解釈はこれに対する一つの解決法を示しています。その問題意識は、プログラムにランタイムエラーが存在しないというような、「安全性の解析」を数学的に示すことが出来ないかということです。プログラムのエラーを大まかに下記のように分類すると、抽象解釈によるプログラム解析の対象は最後のNO.4です。
<エラー種別> <発見する方法>
1.シンタックスエラー コンパイラ
2.コーディングルール違反 従来の静的解析ツール
3.アプリケーションエラー テストデータを作り各種テストにより検出
4.プログラムダウンに至るような致命的エラー 高度なプログラム解析(抽象解釈など)
(零除算、オーバーフローなど)
P.Cousotの言葉によれば、「抽象解釈はソフトウェアの解析と静的検証に使用できる情報システムのセマンティクス(意味論)についての離散的な近似の理論」です。簡単に言えば、プログラムの解析に必要な側面に着目してそれを抽象化(プログラムのセマンティクス)することにより、プログラムを実際に実行することなく検証する手法です。従来の静的解析との大きな違いは、「ソースコード中の命令をトレースし、逐次的に解析するのではなく、プログラムを抽象的な形に近似した領域で解析を行う」ところにあります。
簡単な例で説明すると、x/(x-y)というzero divideの可能性のある式を含むプログラムをチェックする場合、下の図のように抽象解釈では、プログラムの変数の個々の値(図では×の記号)を考えるのではなく、全ての取り得る値を含む近似領域(図では多角形の領域)を考えます。そして、この多角形領域がプログラム変数の存在を禁止されているゾーン(図ではzero divideを示す直線y=x)と交差していないかをチェックすることにより、プログラムの検証を行うという考え方です。この図の場合、交差していないので確実にzero divideは発生しないことが保証されます。
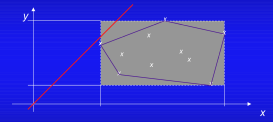
ここには、プログラムの動きを幾何学的に見て判断するという発想の転換が見られます。ここで重要なことは、プログラム変数の可能な存在領域をどのようにして自動的に近似するかということです。
抽象解釈はこの問題に答えるために、プログラム意味論の上に完備束やタルスキの不動点定理及びガロア接続などの数学的議論を展開します。この意味で、抽象解釈はソフトウェアの世界に近代数学が適用された数少ない成功事例の1つと言えます。
ここで、不動点定理やガロア接続が抽象解釈においてどのように関係するかをざっくりと紹介します。
下記の左側のプログラムにおいて、変数(x,y)の存在領域がプログラムの再帰処理により下の右図のように単調増大しているとします。このとき、プログラム変数の可能な存在領域を求めることは、その領域がこれ以上増大しない、すなわち不動点の領域を求めることで得られます。単調増大領域の極限は一般的には漸化式で求まりますが、抽象解釈ではこれを一気に求める手法も考えられています(Widningなど)。変数の値の存在領域は、意味のある範囲で単純な方が良いので、抽象解釈では、このような単純な領域への対応関係としてガロア接続を用います。
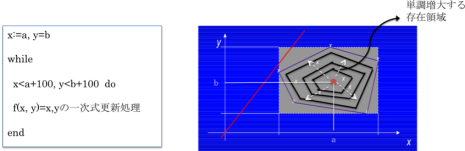
2.抽象解釈の歴史
抽象解釈の手法が提案されたのは1970年代初めの頃です。フランスのP. Cousot, R. Cousot(注)などによりその基礎が確立されました。これを搭載した静的解析ツールは、欧米で商用化されていて(Polyspace等)プログラム解析に威力を発揮しています。

(注)Patrick Cousot:パリのÉcole Normale SupÉrieure(高等師範学校)情報学部教授
Radhia Cousot:Directrice de recherche CNRS &École Normale SupÉrieur
→École Normale SupÉrieure(エコール・ノルマル・シュぺリウール)はフランスの高等教育機関
(グランゼコール)の一つ。著名な哲学者(サルトル他)、文学者(ロマン・ロラン他)、数学者など
を多数輩出。 CNRS:Le Centre national de la recherche scientifique(フランス国立科学研究
センター)1939年設立
3.抽象解釈考:ガロア理論との対比
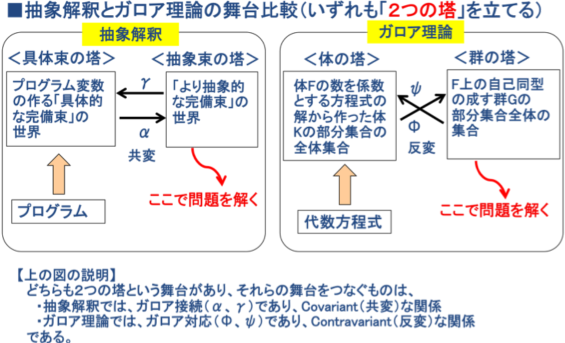
抽象解釈ではガロア接続というガロアの名前が登場するので、下記に抽象解釈の特徴とガロア理論を対比し両者の類似性を考えてみます;

扱う対象は異なるが両者に共通していることは、
「対象の難しさに正攻法で正面から力ずくで攻めるのではなく、その対象の『或る構造(注)』を抽象化し、そこで問題を解くことです。」
(注)着目する視点;
・抽象解釈の場合は、プログラムの変数の値の単調増加性という『束の構造』であり、
・ガロア理論の場合は、方程式の解の持つ『対称性の構造(体と群の構造)』です。
これを図で比較すると、次頁のようになります。
4.エピローグ:抽象解釈への船出
2000年代の始め、米国の計算機科学者Joseph Goguenは理論的なコンピュータサイエンスと実践的なソフトウェアのアプリケーション間に大きな断絶があり、これを理論と実践の間にある"大分水嶺(great divide)"と呼びました。そして、様々な種類の代数(主にカテゴリー論)を使用してコンピュータの使用の理論と実践間の大分水嶺を乗り越える試みをしました。彼はこれを「大分水嶺に代数の花を放る(Tossing Algebraic Flower down the Great Divide)」と表現しました。
抽象解釈もまた、ソフトウェアの世界で数学的理論と実践を結び付けた数少ない事例という意味で興味を惹かれます・・・・
下記は、アイルランドの詩人W.B.イエイツの有名な詩「Sailing to Byzantium(ビザンティウムへの船出)の一部から作成しました;
Sailing to Abstract Interpretation
Software Engineering is no country
for mathematical structure.
Dominated in that great numbers
unclear analysis methods.
All neglect monuments of mathematical
intellect.
Mathematics is but paltry thing,
A tattered coat upon a stick;
Nor is there design method but studying
Descriptions of Natural language or Figures.
No mathematical structure in there
And therefore I have sailed the seas and come
To the holy city of Abstract Interpretation.
抽象解釈への船出
ソフトウェアエンジニアリングは数学的構造
の住める国ではない。
多数の明晰でない分析手法に支配され、
数学的知恵を(適用しようと)省みるものは
いない。
そこでは数学は余計物あつかい
壁に引っ掛けられたコートのようだ
ここで人々が教わる設計手法といえば
自然言語や図式の記述ばかり。
そこに数学的構造はない
それ故わたしはそこを去って
抽象解釈の聖なる都市へと船出したのだ。
